RDP 2015-07: A Multi-sector Model of the Australian Economy 3. Estimation
May 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.28MB
3.1 Data
We estimate the model using quarterly data for the period 1992:Q1–2013:Q4, a total of 88 quarters. The observed variables of the model are: the growth rates of Australian GDP, consumption, investment, public demand, resource exports and non-resource exports and foreign GDP; the growth rates of value-added output in the Australian non-tradeable, non-resource tradeable and resource sectors; trimmed mean CPI inflation and non-tradeable inflation in Australia and inflation abroad; the growth of foreign-denominated resource prices; and the level of the nominal policy interest rates at home and abroad.[7]
We use seasonally adjusted data where available and measure all national accounts data in real terms. We also pre-filter the data by removing the sample mean of each variable prior to estimation. We use standard data sources for all of the Australian variables. For the foreign variables, we used the trade-weighted average GDP growth of Australia's major trading partners; the average inflation of the G7 economies; and the simple average of the policy interest rates in the G3.
3.2 Calibration
We parameterise the model at a quarterly frequency (Table 1). The steady-state rate of productivity growth, µ, is set to 0.8 per cent and the inflation rate to 2.5 per cent at an annualised rate. These values are consistent with the average rate of Australian GDP growth over our sample and the midpoint of the RBA's inflation target. We set the household's discount factor, β, equal to 0.9996. Together, these three parameters imply that the model's steady-state cash rate is equal to 6 per cent.
| Parameter | Description | Value |
|---|---|---|
| Technology and policy | ||
| μ | Steady-state total factor productivity growth rate | 1.008 |
| π | Steady-state inflation rate | 1.0062 |
| Χ | Risk premium coefficient | 0.001 |
| δ | Capital depreciation rate | 0.0175 |
| b* | Governs steady-state trade deficit | 25 |
| g | Governs share of public demand in expenditure | 2.2 |
| Households | ||
| β | Household's discount factor | 0.9996 |
| ωn | Controls share of non-tradeables in domestic final demand | 0.63 |
| ωh | Controls share of non-resource tradeables in domestic final demand | 0.12 |
| ωf | Controls share of imports in domestic final demand | 0.25 |
| ζ | Intersectoral elasticity of substitution in domestic final demand | 0.8 |
| ζ* | Elasticity between domestic and foreign goods overseas | 0.8 |
| η | Labour supply elasticity | 1 |
| σ | Intersectoral labour supply elasticity | 1 |
| Non-traded sector | ||
| αn | Labour share in non-traded sector | 0.7 |
| γn | Capital share in non-traded sector | 0.24 |
| θn | Elasticity of substitution in non-traded sector | 6 |
| Non-resource sector | ||
| αh | Labour share in non-resource traded sector | 0.6 |
| γh | Capital share in non-resource traded sector | 0.32 |
| θm | Elasticity of substitution in non-resource traded sector | 6 |
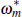 |
Governs share of non-resource tradeable goods that are exported | 2.5 |
| Resource sector | ||
| αz | Labour share in resource sector | 0.2 |
| γz | Capital share in resource sector | 0.25 |
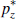 |
Governs share of resources in exports | 2.5 |
| Imports sector | ||
| θf | Elasticity of substitution in imports sector | 6 |
We set the inverse of the Frisch labour supply elasticity, η, equal to 1. This is a standard value in the literature and close to the estimate for Australia in Justiniano and Preston (2010b). We set the parameter governing the willingness of workers to move between sectors, σ, equal to 1, which is consistent with Horvath (2000). With this parameterisation, workers in the model do not view jobs in different sectors as perfect substitutes, but they are willing to move between sectors if relative wage movements are large enough.
We set the parameters governing the share of non-tradeable, non-resource tradeable and imported goods in the domestic final goods basket, ωn, ωm and ωf, to match the share of these goods in nominal GDP. We set the intersectoral elasticity of final demand, ζ, and the elasticity of demand for domestic non-resource goods overseas, ζ*, equal to 0.8. These values are in line with the range of estimates in the literature (Stockman and Tesar 1995; Justiniano and Preston 2010b; Rabanal and Tuesta 2012).
We set the intrasectoral elasticities of substitution for the non-traded, non-resource traded and import sectors, θn, θm and θf, equal to 6. This implies an average mark-up in these sectors of 20 per cent.
We calibrate technological parameters in the production functions of the three domestic production sectors using data on factor incomes for each of these sectors. We set the quarterly depreciation rate of capital in each sector equal to 1.75 per cent, which is around the average value of this parameter in the Australian national accounts. Finally, we set the parameter governing the steady-state level of government spending, g, and that governing the steady-state foreign asset level, b*, to match the average share of public demand in nominal GDP over the sample and the average trade deficit.
Table 2 compares some important steady-state ratios of the model to their averages in the data over our estimation sample. The model successfully captures many of these key features of the data.
| Target | Average 1993–2013 | Model |
|---|---|---|
| Expenditure (per cent of GDP) | ||
| Household consumption | 56.9 | 55.8 |
| Private investment | 21.4 | 22.7 |
| Public demand | 22.5 | 22.5 |
| Exports | 19.5 | 19.6 |
| Imports | 20.6 | 20.6 |
| Production (per cent of GVA) | ||
| Non-tradeable | 64.0 | 64.0 |
| Other tradeable | 26.3 | 23.1 |
| Mining | 9.7 | 12.9 |
| Trade (per cent of exports) | ||
| Resource exports | 40.1 | 40.1 |
| Other exports | 59.9 | 59.9 |
| Investment demand (per cent of private investment) | ||
| Non-tradeable | 58.5 | 58.4 |
| Other tradeable | 27.8 | 27.7 |
| Mining | 13.7 | 13.9 |
3.3 Bayesian Estimation
To estimate the model, we follow standard practice in the DSGE literature and use Bayesian techniques that place informative priors on the estimated parameters.[8] Informative priors are useful because they regularise the posterior distribution of the model so that it remains numerically stable, while also compensating for the brief span of available data and ensuring that the resulting parameter estimates are economically sensible. Within that scope, we tried to make the prior distributions as loose as possible. For instance, most of the AR(1) coefficients are given priors that allow them to take posterior values almost spanning the stable unit interval, while ensuring that they do not collapse to zero or one.
In our estimation, we allow for measurement errors in all variables except for the nominal interest rates in Australia and abroad. Measurement errors account for the possibility that macroeconomic data may be measured with substantial noise.[9]
They also reflect the fact that the economic concepts recorded in official data series may differ from those in the model. We calibrate the variances of the measurement errors so that they correspond to 10 per cent of the variance of each data series.
We use the Metropolis Hastings algorithm to take draws from the posterior distribution of the model's parameters, after using numerical procedures to locate the mode. We take 100,000 draws from the posterior distribution and discard the first 50,000 as a burn-in. The values of the posterior draws indicated that the initial estimate of the posterior mode was adequate. While multiple modes can occur in theory, the use of informative prior distributions makes this possibility remote in practice.
Following Kulish and Rees (2011), we estimate the model in two stages. In the first, we estimate the large economy's parameters. In the second, we estimate the remaining small economy's parameters, taking as given the posterior mean values of the common parameters from the first stage.
Table 3 summarises the results from the first stage of the estimation. Focusing first on the exogenous processes, we find that shocks to the prices of Australia's export commodities are large and persistent, which is a common finding in the literature (Jääskelä and Nimark 2011; Kulish and Rees 2014). Like Justiniano and Preston (2010b) and Kulish and Rees (2011), we find that shocks to overseas output are considerably larger than shocks to overseas inflation and monetary policy. The shocks to overseas output and monetary policy are highly persistent, while the inflation shocks are more transitory.
The coefficients of the foreign Taylor rule imply a strong response to inflation and a modest response to deviations of output from its steady-state level. Although it is difficult to compare these parameters to other studies as our overseas output, inflation and interest rate series represent averages across multiple economies, these estimates appear plausible. The estimated response of resource prices to foreign output shocks is small and not significantly different from zero. Our estimates suggest that the overseas Phillips curve is quite flat – a common finding in the literature.
| Parameter | Prior distribution | Posterior distribution | ||||||
|---|---|---|---|---|---|---|---|---|
| Shape | Mean | Std dev | Mode | Mean | 5 per cent | 95 per cent | ||
| ρξ * | beta | 0.500 | 0.150 | 0.96 | 0.98 | 0.93 | 0.97 | |
| ρe* | beta | 0.500 | 0.150 | 0.31 | 0.33 | 0.18 | 0.49 | |
| ρr* | beta | 0.750 | 0.100 | 0.94 | 0.93 | 0.91 | 0.95 | |
| ϕπ* | normal | 1.500 | 0.100 | 1.37 | 1.47 | 1.12 | 1.80 | |
| ϕy* | normal | 0.125 | 0.050 | 0.22 | 0.21 | 0.14 | 0.28 | |
| ρzy | normal | 0.000 | 0.200 | 0.14 | 0.19 | −0.13 | 0.49 | |
| ϕΔy * | normal | 0.125 | 0.050 | 0.13 | 0.13 | 0.08 | 0.18 | |
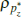 |
beta | 0.500 | 0.150 | 0.94 | 0.93 | 0.90 | 0.97 | |
| κ* | gamma | 1.000 | 0.800 | 1.81 | 3.79 | 0.42 | 7.36 | |
| Standard deviations (× 100) | ||||||||
| σz* | gamma | 0.5 | 0.4 | 5.62 | 5.70 | 4.96 | 6.39 | |
| σy* | gamma | 0.5 | 0.4 | 1.37 | 1.28 | 0.90 | 1.68 | |
| σr* | gamma | 0.5 | 0.4 | 0.06 | 0.07 | 0.05 | 0.09 | |
| σπ* | gamma | 0.5 | 0.4 | 0.19 | 0.20 | 0.15 | 0.24 | |
| σμ | gamma | 0.5 | 0.4 | 0.09 | 0.15 | 0.01 | 0.27 | |
Table 4 shows the parameter estimates for the domestic block. As was the case for the foreign block, the domestic Phillips curves are estimated to be extremely flat. In the context of the model, this indicates a high degree of price rigidity. However, a flat Phillips curve may also be indicative of well-anchored inflation expectations, as discussed in Roberts (2006) and Mishkin (2007). Non-tradeable prices appear to be the most sticky, followed by import prices, with the non-resource tradeable sector exhibiting the most price flexibility. These findings are consistent with Kulish and Rees (2014).
The habits parameter, h, has a posterior mean of 0.77, which is similar to that estimated in Jääskelä and Nimark (2011), and indicative of a large degree of inertia in consumption. The parameter governing the degree of investment adjustment costs, Φ, is estimated to be 1.78, which is less than half as large as the equivalent parameter in Jääskelä and Nimark. This smaller value may be due to the multi-sector structure of our model, which allows investment to respond differently across sectors without necessarily affecting aggregate investment in the economy. The coefficients on the domestic Taylor rule are similar to those on the foreign Taylor rule. Consistent with Lubik and Schorfheide (2007) and Kam, Lees and Liu (2009), we find no evidence that monetary policy in Australia responds directly to exchange rate movements.
| Parameter | Prior distribution | Posterior distribution | ||||||
|---|---|---|---|---|---|---|---|---|
| Shape | Mean | Std dev | Mode | Mean | 5 per cent | 95 per cent | ||
| h | beta | 0.5 | 0.15 | 0.75 | 0.77 | 0.67 | 0.88 | |
| κπn | gamma | 50 | 40 | 0.18 | 0.28 | 0.04 | 0.52 | |
| κπf | gamma | 50 | 40 | 0.79 | 1.16 | 0.23 | 2.01 | |
| κπm | gamma | 50 | 40 | 1.12 | 1.57 | 0.37 | 2.76 | |
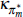 |
gamma | 50 | 40 | 1.24 | 1.89 | 0.29 | 3.45 | |
| χ | beta | 0.3 | 0.15 | 0.23 | 0.24 | 0.11 | 0.38 | |
| Φ | gamma | 4 | 1 | 1.64 | 1.78 | 1.19 | 2.36 | |
| ρr | beta | 0.75 | 0.1 | 0.86 | 0.86 | 0.81 | 0.91 | |
| ϕπ | normal | 1.5 | 0.2 | 1.26 | 1.37 | 0.99 | 1.68 | |
| ϕy | normal | 0.125 | 0.05 | 0.12 | 0.12 | 0.04 | 0.20 | |
| ϕΔy | normal | 0 | 0.025 | 0.05 | 0.05 | 0.01 | 0.08 | |
| ϕq | normal | 0 | 0.05 | 0.00 | 0.00 | −0.01 | 0.01 | |
| ρg | beta | 0.5 | 0.15 | 0.33 | 0.35 | 0.17 | 0.52 | |
| ρξc | beta | 0.5 | 0.15 | 0.72 | 0.67 | 0.50 | 0.84 | |
| ρϒ | beta | 0.5 | 0.15 | 0.31 | 0.36 | 0.15 | 0.55 | |
| ρψ | beta | 0.5 | 0.15 | 0.87 | 0.83 | 0.76 | 0.90 | |
| ρan | beta | 0.5 | 0.15 | 0.77 | 0.69 | 0.53 | 0.84 | |
| ρam | beta | 0.5 | 0.15 | 0.53 | 0.47 | 0.32 | 0.63 | |
| ρaz | beta | 0.5 | 0.15 | 0.87 | 0.83 | 0.71 | 0.95 | |
| Standard deviations (× 100) | ||||||||
| σg | gamma | 0.5 | 0.4 | 2.15 | 2.20 | 1.88 | 2.50 | |
| σξc | gamma | 0.5 | 0.4 | 2.04 | 2.37 | 1.44 | 3.24 | |
| σϒ | gamma | 0.5 | 0.4 | 5.38 | 5.63 | 3.96 | 7.29 | |
| σψ | gamma | 0.5 | 0.4 | 0.50 | 0.63 | 0.37 | 0.89 | |
| σan | gamma | 0.5 | 0.4 | 2.68 | 2.64 | 2.17 | 3.13 | |
| σam | gamma | 0.5 | 0.4 | 5.25 | 5.19 | 4.35 | 6.07 | |
| σaz | gamma | 0.5 | 0.4 | 1.77 | 1.79 | 1.54 | 2.05 | |
| σr | gamma | 0.5 | 0.4 | 0.11 | 0.12 | 0.10 | 0.13 | |
| σπn | gamma | 0.5 | 0.4 | 0.21 | 0.22 | 0.18 | 0.26 | |
| σπf | gamma | 0.5 | 0.4 | 0.41 | 0.43 | 0.21 | 0.68 | |
| σπm | gamma | 0.5 | 0.4 | 0.73 | 0.72 | 0.36 | 1.09 | |
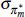 |
gamma | 0.5 | 0.4 | 3.54 | 3.69 | 3.09 | 4.31 | |
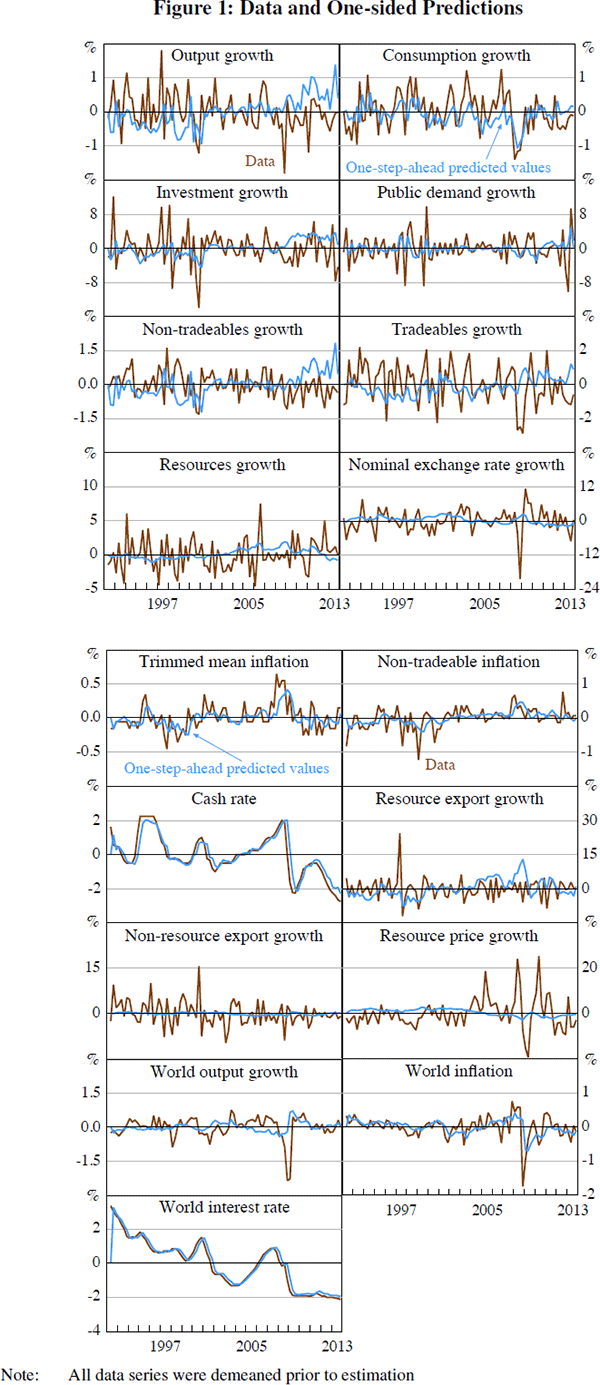
Figure 1 shows the data used in estimation and one-sided Kalman filtered one-step-ahead predictions from the model. For most series, the model captures the low-frequency variations in the data reasonably well, but it struggles to match some of the high-frequency movements, particularly for volatile variables such as the exchange rate or resource prices. The model also over-predicts GDP growth in the period after the global financial crisis, largely because of a sequence of large prediction errors for the growth rate of the non-tradeable sector. Understanding the causes of these prediction errors and improving the fit of the model in this dimension will be an important part of our ongoing model development program.
Appendix C contains plots of the posterior and prior distributions of the parameters for the domestic economy. Most of the parameters appear to be reasonably well identified, with the posterior distribution being more concentrated than the prior distribution. Appendix D contains plots of the shocks, calculated at the posterior mean of the model parameters.
Footnotes
Appendix B contains a description of the data series used in estimation. [7]
See An and Schorfheide (2007) for a description of Bayesian DSGE model estimation. We use the MATLAB package Dynare to estimate the model. [8]
See Rees, Lancaster and Finlay (forthcoming) for an illustration of measurement error in Australian GDP. [9]