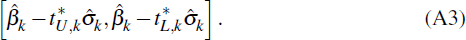RDP 2015-04: The Sticky Information Phillips Curve: Evidence for Australia Appendix A: Confidence Intervals for Econometric Forecasts

Ordinary standard errors generated by estimation of the SIPC with the econometric forecasts do not take forecast uncertainty into account. This is the generated regressors problem discussed by Pagan (1986). To allow for uncertainty caused by estimation of the forecasts, the bootstrap procedure outlined by Kahn and Zhu (2006) is followed. The first step in the procedure requires generating alternate histories of the data. The vector autoregression model

is estimated using each of the forecast and explanatory variables listed in Table 1, for the period 1964–2013. The lag length is set at 8 quarters, guided by the AIC criteria. The first alternate history of data is created by repeated resampling (with replacement) from the vector of estimated residuals 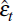, using the first L-quarters of data for the lagged dependent variables. Data for an initial burn-in-period of 100 quarters is discarded, leaving a simulated set of data for the period 1964–2013. This procedure is repeated N = 500 times to produce a set of alternate histories of data.

For each history of data, the forecast procedure outlined in Section 3.1 is used to estimate econometric forecasts for CPI inflation, underlying inflation and the change in the output gap. Use of each alternate set of forecasts to estimate the SIPC produces a distribution of parameter estimates and standard errors for each regression coefficient. For each set of data i and regression parameter β_k the test statistic

is calculated, where 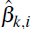is the estimated regression coefficient for parameter k using alternate history of data i, 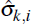is its estimated standard error, and 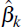is the parameter estimate using the observed data. Taking the 2.5 and 97.5 percentiles of 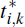produces bootstrapped 95 per cent critical values 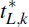and 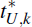for regression parameter k. Using these critical values, a percentile-t interval can be calculated for regression parameter k:

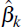Note that the percentile-t confidence interval is not guaranteed to contain the parameter estimate . For example, suppose each bootstrapped estimate 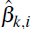> 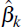, then 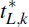> 0 and the upper bound of the confidence interval is less than the parameter estimate 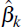.