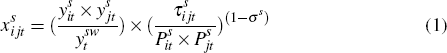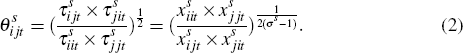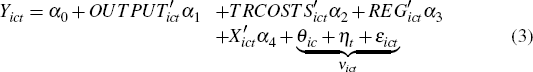RDP 2014-07: International Trade Costs, Global Supply Chains and Value-added Trade in Australia 5. Regression Analysis
August 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 977KB
In this section we undertake econometric analysis to examine the determinants of the Australian supply chain. In particular, we assess the extent to which changes over time in vertical fragmentation have been driven by exogenous domestic forces (e.g. product market deregulation) and external forces (e.g. falling international transport costs).
5.1 Hypotheses
Jones, Kierzkowski and Lurong (2005) provide a useful conceptual framework for studying the determinants of vertical fragmentation. Suppose a firm produces a particular final good in a vertically integrated process, in which all activity takes place in one location. As the scale of production increases, the firm may find it optimal to divide the production line into different fragments that may be located elsewhere. The total cost of production may be lowered by outsourcing, for example, a stage that makes relatively high use of unskilled labour, to another location in which the unit labour costs of unskilled labour are relatively low. But the fragmentation of production is costly as it also requires services that link each production stage, such as transportation and communication activities.
In this framework, it is optimal for the firm to fragment production if the lower costs due to shifting resources to locations with relatively low unit labour costs outweigh the higher costs associated with the greater service link activities. For a graphical exposition of the model and more detailed analysis, see Jones et al (2005).
From this simple model we can derive three testable hypotheses:[19]
- Fragmentation rises as an industry (or economy) grows
- Fragmentation rises as trade (or service link) costs fall
- Offshoring (or the share of production that occurs in other countries) rises as international trade costs fall.
Clearly, information on international and domestic trade costs is required to test these hypotheses. Before turning to the regression framework, we therefore need to briefly discuss how we measure international and domestic trade costs.
5.2 International Trade Costs
Trade costs can be inferred from an economic model linking trade flows to observable variables and unobserved trade costs. The standard model in the international macroeconomic literature is the ‘gravity model’. This model assumes that the level of bilateral trade between an importing country and an exporting country is a function of the level of economic activity in each of the two countries, as well as bilateral trade barriers. We follow the recent literature by estimating international trade using the inverse gravity model, which essentially ‘flips’ the gravity model on its head (Novy 2013). International trade costs can be derived from a micro-founded gravity equation (Anderson and van Wincoop 2003):
where, for each industry s in year t, 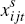 denotes nominal exports from country i
to country j,
denotes nominal exports from country i
to country j, 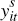 and
and 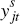 denote the levels of
output produced in country i and country j respectively,
denote the levels of
output produced in country i and country j respectively,
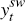 denotes world output,
denotes world output, 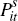 and
and 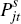 are the aggregate price
indices of country i and country j respectively,
are the aggregate price
indices of country i and country j respectively, 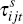 is the bilateral trade
cost, σs > 1 is the elasticity of substitution
across goods within the industry.
is the bilateral trade
cost, σs > 1 is the elasticity of substitution
across goods within the industry.
Algebraic manipulation of Equation (1) (provided in Appendix D) gives an expression for international
trade
costs 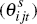 as a function of bilateral international trade, domestic (or intra-national)
trade and the elasticity of substitution in consumption between goods:
as a function of bilateral international trade, domestic (or intra-national)
trade and the elasticity of substitution in consumption between goods:
The definition of international trade costs combines the ratio of domestic to bilateral trade with an exponent that involves the industry-specific elasticity of substitution. In an industry with highly elastic goods, consumers are very sensitive to variations in price and so a small price rise induced by bilateral trade costs can lead to a high ratio of domestic to bilateral trade. Therefore, the ratio reflects not only bilateral trade frictions but also the extent of product differentiation.
The implied estimates of international trade costs include all the costs involved in moving goods between two countries relative to the cost of selling the goods domestically. These trade costs include factors such as transportation costs, policy barriers, information costs, contract enforcement costs, and local distribution costs. The more two countries trade with each other, the lower is the measure of relative trade costs, all other things being equal.
To compute trade costs across industries, countries and time, we need data on the bilateral export flows between countries i and j as well as the domestic trade within each country. For each industry and year, the domestic trade of each country is assumed to be given by the level of gross output minus total exports to the rest of the world. These data are readily available in the WIOD.
As Equation (2) suggests, the trade cost measures also require an estimate of the elasticity of substitution between goods within each industry. We follow Anderson and van Wincoop (2004) and Novy (2013) in setting the elasticity of substitution equal to eight across all industries and countries. The estimated level of trade costs is very sensitive to this choice of elasticity. However, because the elasticity does not vary with time, it has little effect on estimates of the change over time in trade costs. And, because our econometric analysis depends on the variation over time in trade costs, it is not affected by the choice of parameter value for the elasticity of substitution.
Our estimates imply that, since the mid 1990s, world international trade costs have averaged about 169 per cent of what it would cost for the same trade to occur domestically. Furthermore, we find international trade costs are around 132 per cent of the value of domestic production for manufactured goods and 234 per cent for services. This estimate may seem large at first glance. The difference in costs reflects not only shipping costs, but tariff and non-tariff barriers, as well as other less observable costs, such as those associated with using different currencies or any language barriers. Furthermore, the estimate is an average for all goods and services produced around the world, some of which may not be traded due to prohibitively high trade costs.
To understand the intuition behind these estimates, consider the following hypothetical example. Suppose the domestic cost of producing a traded good in country A is $10. Further, suppose that the ‘ad valorem’ cost for international shipping from country A to B is equal to 2.5. This cost captures factors including transportation costs, tariffs and costs associated with converting currencies. The implied landed import price of the traded good in country B would be $25 (i.e. landed import price = domestic production cost × international shipping cost). Further, suppose that the cost of domestic shipping in country B is 1.4. This captures local distribution costs associated with the domestic transport, wholesale and retail trade sectors. This would imply that the final sale price in country B is $35 (i.e. final sale price = landed import price × local shipping cost). Moreover, note that the ad valorem cost of bilateral trade from country A to B equals 3.5 (i.e. international shipping cost from A to B × domestic shipping cost in B).
Now consider the opposite direction of trade. For simplicity, let the domestic cost of producing the good in country B again be equal to $10. Further, let the ad valorem international shipping cost from country B to A be a bit lower at 1.5. The landed import price in country A would be $15. Let the local shipping (ad valorem) cost in country A be a bit higher at 1.6. This would imply that the final sale price in country A is $24. Again, the total bilateral (ad valorem) trade cost from country B to A would be equal to 2.4 (i.e. international shipping cost from B to A × domestic shipping cost in A).
In this example, the ad valorem international trade cost equals 93.6 per cent. There are two ways to think about this estimate. First, it measures the ratio of total bilateral trade costs to domestic trade costs (i.e. (3.5×2.4)/(1.4×1.6)−1). Second, it measures the international component of trade costs net of local distribution trade costs in each destination country (i.e. 2.5×1.5−1).
Our estimates of world international trade costs are similar, albeit somewhat higher, than comparable estimates from the literature. For example, using a different trade database, Miroudot, Sauvage and Shepherd (2013) estimate international trade costs of 95 per cent for manufactured goods and 169 per cent for services. Chen and Novy (2011) estimate international trade costs for manufactured goods to be around 110 per cent. Furthermore, using US data, Anderson and van Wincoop (2004) estimate international trade costs for manufactured goods to be about 74 per cent, on average.[20]
To aid comparability in the estimates of international trade costs across sectors, countries and over time, and given the caveat that the estimates are sensitive to the chosen elasticity of substitution, we index the levels of the trade cost estimates in the subsequent graphical analysis. More specifically, in Figure 12, the level of global international trade costs in 1995 is set equal to 100. In Figure 13, the level of global manufactured goods trade costs in 1995 is set equal to 100.
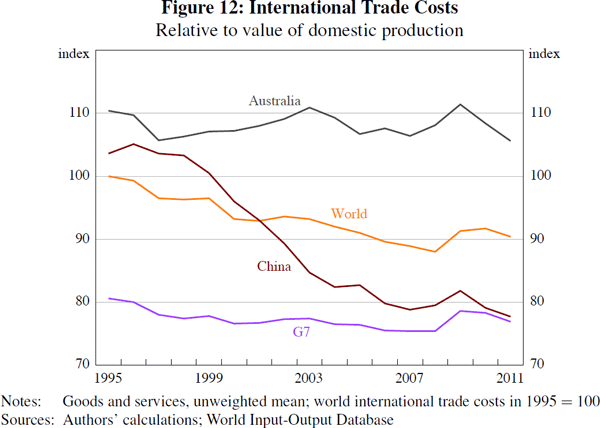
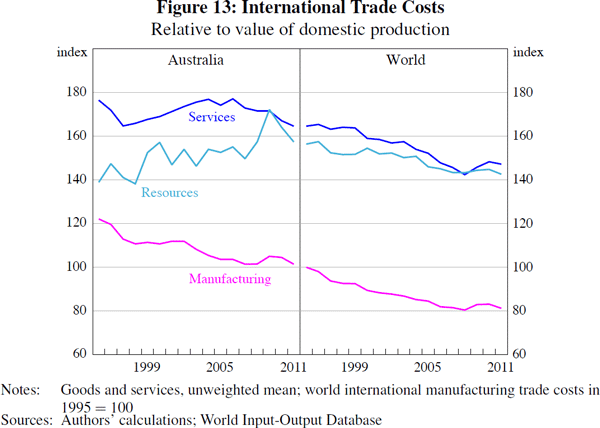
By international standards, Australia has a relatively high level of trade costs, particularly in relation to the G7 economies. Australia's trade costs are estimated to be around 17 per cent higher than the world average in 2011. This reflects both Australia's geographic isolation, as goods and services are traded over greater distances on average, and its composition of trade, because resources are estimated to be more costly to trade than manufactured goods (Figure 13).
Our estimates also imply that world international trade costs have fallen by about 10 per cent over the past two decades, with a faster pace of decline for developing economies and manufactured goods. For most advanced economies, much of the reduction in international trade costs occurred during the 1970s and 1980s (Jacks, Meissner and Novy 2008). Since the mid 1990s, the average level of trade costs is estimated to have fallen by almost 5 per cent for Australia and the G7 economies.[21]
5.3 Domestic Trade Costs and Sectoral Regulation
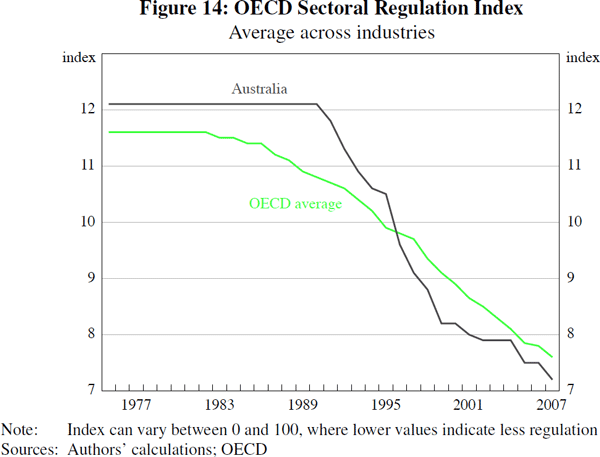
We proxy the level of domestic trade (or service link) costs using the OECD sectoral regulation index. This provides an internationally comparable measure of the degree to which government policies inhibit the use of intermediate inputs in a particular industry and country. The indicators effectively measure the ‘knock-on’ effects of regulation in non-manufacturing sectors on all sectors of the economy.
The indices are constructed as averages of the indicators of regulation for non-manufacturing industries weighted by the share these industries represent in supplying intermediate inputs to each sector. The ‘knock-on’ effect of regulation on the aggregate economy is a function of two factors: i) the extent of anti-competitive regulation in a particular sector; and ii) the importance of that sector as a supplier of intermediate inputs to other sectors in the economy.
The sectoral regulation index does not capture all sources of domestic trade frictions, only those that are affected by government policy. But, given that much of the increase in fragmentation in the advanced economies (including Australia) coincided with a period of extensive microeconomic reform in the 1990s (e.g. product market deregulation), regulations are likely to be an important component of domestic trade frictions. Moreover, to our knowledge, the link between government regulation and vertical fragmentation has not been studied before.
There are a few channels through which sectoral regulation and the degree of fragmentation might be linked: regulation can affect i) the costs of entry for new firms that rely on the regulated intermediated inputs; ii) the extent to which firms outsource their inputs; iii) the organisation of work within each firm; and iv) the allocation of resources between firms. Previous research has used these regulation indices to study the effect of anti-competitive regulation on productivity growth (Bourlès et al 2013) and export performance (Amable and Ledezma 2013), but not to measure the effect of government regulation on fragmentation. For more details on the construction of the indices, see Appendix E.
On average, the level of sectoral regulation has been gradually declining across all OECD countries and industries since the mid 1970s (Figure 14). Sectoral regulation in Australia has followed a similar trend, although deregulation started a little later (in the early 1990s) and has occurred at a faster pace than the OECD average.[22]
5.4 Modelling Framework
To test our hypotheses about the extent of vertical fragmentation and offshoring, we estimate panel regressions of the following form:
where the dependent variable (Yict) is either the fragmentation index, measured as the (log level) of the number of production stages in industry i in country c in year t (FRAGict), or the offshoring index, measured as the ratio of foreign production stages to total production stages (OFFSHOREict).[23]
Based on our hypotheses, the key explanatory variables include, for each industry, country and year, the (nominal) level of domestic output (OUTPUTict), international trade costs (as a share of the value of domestic production) (TRCOSTSict) and the OECD regulation index (REGict).
To reiterate the hypotheses outlined earlier, we expect there to be a positive correlation between the scale of production in an industry or economy and the level of fragmentation. Furthermore, there should be a negative correlation between the domestic regulation index and the overall level of fragmentation. Similarly, the level of offshoring and international trade costs should be inversely related. If foreign outsourcing is an imperfect substitute for domestic outsourcing, then lower trade costs may also increase the overall level of fragmentation.
In each regression specification, we also include a set of control variables (Xict) that the literature has identified as being important in explaining vertical fragmentation. These control variables (and their associated measurement) include:
- Trade to GDP ratio: the ratio of exports and imports to gross value-added
- Productivity: the level of labour productivity, measured as gross value-added divided by the total number of hours worked
- Physical capital intensity: the level of capital stock divided by gross output
- Human capital intensity: the share of total hours worked by high-skilled workers.
International trade can have two opposite effects on the level of vertical fragmentation. International trade provides new opportunities to reduce costs by shifting production processes abroad, in which case we might expect a positive effect of trade on the fragmentation of production. However, much of this effect is likely to be already captured by the inclusion of international trade costs in the set of explanatory variables. An increase in trade can also reduce the measure of fragmentation if it reduces the relative price of intermediate goods and the total amount of expenditure on these goods, thereby reducing the share of value-added associated with upstream stages.[24]
Industries with low levels of productivity may have greater potential for fragmentation and offshoring of production stages. This would suggest that there should be an inverse relationship between both the level of productivity and fragmentation, and productivity and offshoring, across industries and countries.
The extent of vertical fragmentation can also depend on physical capital intensity. Capital-intensive industries rely more on centralised investment decisions and are thus more likely to be integrated, whereas decisions taken by suppliers are relatively more important in labour-intensive industries, leading to more offshoring in these industries (Antràs 2003). We therefore predict that higher physical capital use will be associated with less fragmentation.
Human capital intensity – measured through skill intensity and the complexity of tasks – can also affect the level of fragmentation. In general, more complex tasks are more likely to be performed within the firm (Costinot, Oldenski and Rauch 2011). Consequently, industries and countries with lower levels of human capital intensity should be more fragmented.
Finally, the regression specification also includes a composite error term (νict), which consists of a country-industry specific effect (θic), a year fixed effect (ηt) and an idiosyncratic term (εict). Country-industry fixed effects are included to control for unobserved factors that vary by country and industry but not by time. This would include factors such as geographic location and the nature of the industry's product. The year fixed effects capture factors that affect all countries and industries at a given point in time, such as the global financial crisis.
Our final sample consists of 28 industries in each of 24 countries covering the period from 1995 to 2007. While the WIOD covers 35 industries in 40 countries and spans the period from 1995 to 2011, some of our explanatory variables are obtained from alternative data sources that restrict our sample both in terms of the time series and the cross-section. Most importantly, the OECD sectoral regulation index is only available up to 2007 and covers only OECD countries. Finally, for each of the key variables – namely, the fragmentation index, the OECD regulation index and international trade costs, the top and bottom 1 per cent of observations have been removed to minimise the impact of outliers. Table 5 summarises the key data used in the regression analysis.
| Variable | Mean | Median | 25th pct | 75th pct | Std dev |
|---|---|---|---|---|---|
| Fragmentation (no of stages) | 2.1 | 2.2 | 1.8 | 2.4 | 0.4 |
| International fragmentation (%) | 25.1 | 21.5 | 13.7 | 33.0 | 15.3 |
| Upstreamness (no of stages) | 2.2 | 2.2 | 1.7 | 2.6 | 0.6 |
| International trade costs (%) | 231.0 | 198.3 | 138.3 | 297.4 | 121.9 |
| Sectoral regulation (index) | 15.1 | 10.6 | 6.6 | 20.3 | 11.7 |
| Output (US$m, log level) | 9.1 | 9.3 | 7.7 | 10.6 | 2.2 |
| Trade to GDP ratio (%) | 94.0 | 42.7 | 6.8 | 135.4 | 127.5 |
| Productivity (US$m per hour worked, log level) | 3.1 | 3.2 | 2.6 | 3.7 | 0.9 |
| High-skilled labour share (%) | 17.8 | 13.9 | 8.4 | 24.2 | 12.6 |
| Capital stock ratio (%) | 23.5 | 18.5 | 12.1 | 29.9 | 16.9 |
|
Sources: OECD; World Input-Output Database |
|||||
5.5 Regression Results
The regression output from estimating Equation (3) is shown in Table 6.
| Fragmentation | Offshoring | ||||
|---|---|---|---|---|---|
| OLS (1) |
Fixed effects (2) |
OLS (3) |
Fixed effects (4) |
||
| Output | 0.002 (0.32) |
0.072*** (5.85) |
−0.034*** (−5.00) |
0.005 (0.41) |
|
| International trade costs | −0.075*** (−7.70) |
0.005 (1.41) |
−0.023** (−2.51) |
−0.028** (−2.43) |
|
| Sectoral regulation | −0.135 (−1.57) |
−0.198*** (−2.83) |
−0.154* (−1.73) |
−0.024 (−0.48) |
|
| Trade-to-GDP ratio | 0.014*** (3.59) |
0.000 (0.03) |
0.028*** (3.40) |
0.006*** (3.38) |
|
| Productivity | −0.030** (−2.17) |
−0.116*** (−5.74) |
0.033** (2.09) |
0.024** (2.21) |
|
| High-skill labour share | −0.346*** (−3.62) |
0.056 (0.98) |
−0.077 (−1.17) |
−0.089 (−1.07) |
|
| Capital stock ratio | 0.039 (1.12) |
−0.003 (−0.76) |
−0.084*** (−2.96) |
−0.010 (−1.36) |
|
| Time fixed effects | Y | Y | Y | Y | |
| Country-industry fixed effects | N | Y | N | Y | |
| Within R2 | 0.374 | 0.219 | |||
| R2 | 0.536 | 0.974 | 0.440 | 0.950 | |
| Observations | 9,671 | 9,671 | 9,671 | 9,671 | |
| Notes: Standard errors are two-way clustered by industry and country; t statistics are in parentheses; *, ** and *** denote statistical significance at the 10, 5 and 1 per cent levels, respectively | |||||
First, considering the determinants of the overall level of fragmentation (columns (1) and (2)), we find, as predicted, that output is positively correlated with fragmentation across countries and industries. The fixed effects estimates imply that a 1 per cent higher level of output is associated with an increase of about 7.2 per cent in the number of production stages, on average. This is equivalent to an increase of about 0.15 of a production stage, on average.
The OLS estimates also indicate that lower international trade costs are associated with significantly higher levels of vertical fragmentation, on average (column (1)). But the effect is not statistically significant and of the opposite sign when country-industry fixed effects are included (column (2)).
The level of anti-competitive regulation is negatively associated with the level of fragmentation across countries and industries (columns (1) and (2)). In other words, when a particular country lowers regulations on intermediate inputs within a given industry, this increases the use of intermediate inputs and hence the number of production stages in that industry. This suggests that fragmentation can be affected by the extent of domestic trade frictions. The fixed-effects estimates indicate that a 1 per cent decrease in sectoral regulation is associated with a 0.2 per cent increase in the number of production stages per annum, on average. Given that the degree of regulation has fallen by 0.4 per cent and the number of production stages has risen by 0.3 per cent each year, on average, since the mid 1990s, this implies that government deregulation may have contributed about 25 per cent (=0.4×0.2/0.3) to the increase in fragmentation around the world.
Considering the determinants of offshoring (columns (3) and (4)), we find little evidence that the level of output is a significant determinant. If anything, the OLS estimates point to a negative correlation between the level of output and the foreign share of production stages (column (3)), although the effect is positive and not statistically significant when country-industry fixed effects are included (column (4)).
More notably, lower trade costs are associated with higher offshoring (columns (3) and (4)). The fixed-effects estimates suggest that a 1 percentage point decline in international trade costs (measured on an ad valorem basis) is associated with a 0.028 percentage point increase in the share of production stages that are outsourced overseas, on average. Given that trade costs have fallen by 1.3 percentage points per annum since the mid 1990s and the share of production stages located overseas has risen by 0.2 percentage points over the same period, this suggests that the trend decline in global trade costs has contributed about 16 per cent (=1.3×0.028/0.2) to the rise in offshoring.[25]
We also find that, within countries and industries, fragmentation is positively correlated with the trade to GDP ratio. In contrast, countries and industries with high levels of labour productivity are, overall, less fragmented (columns (1) and (2)) but have a greater share of production stages sourced overseas (columns (3) and (4)). The relationship between human capital intensity and fragmentation is ambiguous. The OLS estimates indicate that across countries and industries, skill intensity is negatively associated with fragmentation (column (1)) while the fixed-effects estimates point to a positive correlation (column (2)).
Footnotes
In essence, there are three key assumptions in the model that generate increasing returns to scale in production and, in turn, deliver the three stated hypotheses. First, there is constant returns to scale (and hence constant marginal costs) within each production fragment. Second, the fragments vary in terms of factor endowments and productivities, such that marginal costs are lower in some fragments than in others. Third, the costs of services to link different stages of production mainly comprise fixed costs, so that service link costs do not rise in proportion to output. [19]
Moreover, they find that total trade costs are, on average, around 170 per cent, with 55 per cent due to local (retail and wholesale) distribution costs and 74 per cent due to international trade costs (i.e. 1.7=1.55×1.74−1). The estimate of international trade costs can be further broken down into 21 per cent due to shipping costs and 44 per cent due to border-related trade barriers (i.e. 1.7=1.55×1.21×1.44−1). [20]
It also appears that the global financial crisis caused an upward spike in world international trade costs, which may be related to disruptions to supply-chain financing at the time (Chor and Manova 2012). Alternatively, there may have been a decline in demand for goods and services that involve relatively low trade costs and this change in the composition of trade may have affected the aggregate estimates. [21]
The OECD estimates suggest that, across countries, the level of sectoral regulation is highest in Belgium, Poland and the Slovak Republic and lowest in Denmark, Sweden and the United States. Across industries, regulation is highest in industries such as utilities, transport and storage, and post and telecommunications, and lowest in education, real estate, and health and social work. [22]
The output from estimating the same specification for other supply chain indicators – namely, the level of upstreamness and the VAX ratio – is shown in Appendix F. [23]
However, this negative price effect will only occur if there is low substitution between outsourced intermediate goods and intermediate goods produced within the firm. Otherwise, the lower relative price of outsourced goods should stimulate demand, leading to a positive volume effect of trade on the share of outsourced intermediate goods. In any case, we estimated regression models that included the ratio of intermediate input prices to gross output prices in the set of control variables and the results barely changed. [24]
We find very similar results for the effect of economic activity and trade costs on vertical fragmentation when we drop the regulation indices and, as a result, broaden the sample to include non-OECD countries and the period since 2007. We also get similar results when we estimate the model based on a lower frequency time series. In particular, we collapse the data to two time periods – pre- and post-2001 – and examine the effect of changes in output, trade costs, and regulation on vertical fragmentation over these two periods. This alleviates any potential stationarity problems and is a useful cross-check given that some of the underlying WIOD data are estimated rather than actual input-output data. [25]