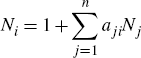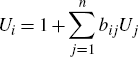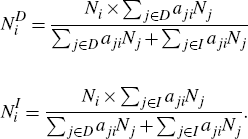RDP 2014-07: International Trade Costs, Global Supply Chains and Value-added Trade in Australia Appendix B: Construction of Supply Chain Statistics

The measures for ‘fragmentation’ and ‘upstreamness’ outlined by Fally (2012) and Antràs, Chor, Fally and Hillberry (2012) are based on input-output methodology. The product of any sector can be used either for final consumption or as an input into further production (intermediate consumption). For a total of n sectors,^[27] the value of the gross output Y_i for sector i ∈ {1,2,,n} can be expressed as the sum 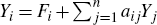, where F_i denotes its use as a final good and a_ij denotes the number of units of sector i inputs required to produce one unit of sector j's output.

The intermediate and final uses of all sectors can be represented in matrix notation as Y = F + AY where Y and F are n×1 column vectors with Y_i and F_i as their respective row i entries, and A an n × n matrix with a_ij as its (i, j)-th element (the technical requirements matrix). The ‘Leontief inverse’ relates total production to final use (or final demand): Y = (I − A)⁻¹F.

The difference between the total value of sector j's intermediate inputs and the total value of sector j's output is equivalent to the ‘value-added’ of that sector (the value contributed by factors of production). That is, 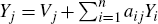, where V_j is the value-added of sector j. This can be represented in matrix notation as Y = V + BY, where V is an n × 1 column vector with V_i as its row i entries and B an n × n matrix with b_ij = a_ijY_j/Y_i as its (i, j)-th element (the allocations matrix). The ‘Ghosh inverse’ relates total production to value-added: Y = (I − B)⁻¹ V.

The ‘fragmentation’ and ‘upstreamness’ measures use the relationships between final demand, intermediate production and value-added to measure the ‘length’ of upstream and downstream supply chains as a weighted average number of production stages. They provide a specific interpretation for the traditional measures of total forward and backward linkages in traditional input-output theory (Miller and Blair 2009).

The ‘fragmentation’ of sector i, denoted N_i, measures the ‘average’ number of stages of production involved for sector i's output, or the length of the upstream supply chain. Production with no inputs involves one stage; production requiring intermediate inputs involves one stage plus the number of stages involved in each input's production, with each input's number of stages weighted according to the share of overall value-added contributed by that input. This describes a system of equations where

or in matrix notation, N = (I−A^T)⁻¹1, for an n × 1 column vector of fragmentation measures N and an n × 1 column vector of ones 1. This measure will be at least one (where there are no intermediate inputs) and rises according to the proportion of a product's value that is added by intermediate inputs, and by the length of these inputs' own supply chains.

As a summary of the nature of a production chain, this fragmentation measure has several shortcomings; it can only capture vertical fragmentation, not horizontal fragmentation, and therefore does not measure the number of suppliers involved at each stage, only the number of stages. It does not take firm ownership into account and will be unaffected if a single firm is responsible for multiple production stages.

Another issue is the treatment of imports. While the WIOD accounts for imported inputs using a multi-country input-output table, single-country input-output tables can treat imported inputs in one of two ways; direct allocation, which excludes imports from the values of inter-industry transactions; and indirect allocation, which includes them. The fragmentation index is best applied to national input-output tables that use indirect allocation of imports, as these tables better reflect the technological input requirements of the industry. The resulting index is accurate on the assumption that the supply-chain characteristics of foreign producers are comparable to those of domestic producers. While this assumption may not be correct, any bias in the index values is likely to be smaller than the difference with the index values found when using direct-allocation tables, which in Australian data is generally insignificant.

The ‘upstreamness’ of sector i, denoted U_i, measures the ‘average’ number of stages of production between the production in sector i and final use, or the length of the downstream supply chain. Production that goes entirely to final use involves one stage; production that goes in part to intermediate use involves one stage plus the number of stages involved in the intermediate uses, with each intermediate use's number of stages weighted according to that use's share of sector i's total output. This describes a system of equations where

or in matrix notation, U = (I − B)⁻¹ 1, for an n × 1 column vector of upstreamness measures U and an n × 1 column vector of ones 1. This measure will be at least one (where none of the output goes toward intermediate use) and rises according to the proportion of the sector's output that goes toward intermediate use, and by the length of these intermediate uses' own supply chains.

The elements of the allocations matrix B, b_ij = a_ijY_j/Y_i, give the total share of sector i's output that goes toward intermediate use by sector j. In an open economy, intermediate and final uses for sector i include the uses of imports belonging to that sector, meaning that it may be more appropriate to consider shares of the sum of domestically produced and imported output. Similarly, in an open economy, ‘final use’, as opposed to ‘intermediate use’, includes exports, which may actually be used for intermediate use in another country, and the treatment of exports as final use may distort the measure. For this reason it may be more appropriate to consider the intermediate-use and final-use shares of domestically absorbed output (in this way, we are implicitly assuming that the downstream supply chains for exports have the same characteristics as the downstream supply chain for domestic output, similar to how assumptions are made for intermediate inputs in the fragmentation measure). Another consideration is the part of output that goes to changes to inventories, which is a component of ‘final demand’ despite representing an absence of effective demand. For our upstreamness measures we use a modified allocations matrix with b_ij = a_ijY_j/(Y_i + M_i − X_i − T_i), where M_i, X_i and T_i represent sector i's imports, exports and inventory changes respectively.

The lengths of upstream and downstream supply chains as represented by the fragmentation and upstreamness measures can be divided into components. Where the input-output table includes the sectors of multiple countries, these components may be the domestic and international sections of the supply chain. For example, for n_D domestic sectors j ∈ D and n_I international sectors j ∈ I the international and domestic components of sector i's fragmentation measure (that is, their upstream supply chain), denote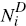d and 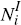, can be given as

The upstreamness measure can be similarly decomposed, giving the domestic and international components of the downstream supply chain.

The fragmentation and upstreamness measures are sensitive to the level of aggregation, that is, the number of sectors used. Where fragmentation or upstreamness measures are available at a disaggregated level, measures can be made for more aggregated sectors by taking a weighted average of the measures of the component industries, weighting the fragmentation measure of each industry by its share of the aggregate sector's total final demand and weighting the upstreamness measure of each industry by its share of the aggregate sector's total value-added. Aggregation of industries into sectors introduces bias for the fragmentation measure where the component industries of a sector differ systematically in the allocation of their output, and introduces bias for the upstreamness measure where the component industries of a sector differ systematically in their input requirements. For a closed economy at the highest level of aggregation (one sector for the whole economy), both measures will converge to the ratio of gross output to value-added (or final demand). For an open economy, the gross output to value-added ratio will overstate the aggregate economy-wide measures of fragmentation and upstreamness if net exports are positively correlated with either measure and will understate these measures if there is a negative correlation (see Fally (2012)).

Footnote

In the case of a multi-country input-output table, the same sector in different countries are simply treated as different sectors; we do not require separate notation to specify the country. [27]