RDP 2013-11: Issues in Estimating New-Keynesian Phillips Curves in the Presence of Unknown Structural Change 4. Simulation Experiments
September 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 587KB
4.1 Parameter Values
In the experiments we report on later, some parameters are assumed to be constant and are thought to apply to the model at a quarterly frequency. These are summarised in Table 1 below.
| Parameter | Description | Value |
|---|---|---|
| α | NKPC parameter on lagged inflation | 0.70 |
| γ | NKPC parameter on expected inflation | 0.29 |
| s = α + γ | Sum of lagged and expected inflation parameter | 0.99 |
| δ | Slope of NKPC | 0.10 |
| ρ | Persistence of the output gap | 0.70 |
| d | Interest rate sensitivity of aggregate demand | −0.10 |
| λ1 | Policy rule parameter: persistence of the interest rate | 0.70 |
| λ2 | Policy rule parameter: response to output gap | 0.50 |
| λ3 | Policy rule parameter: response to inflation | 1.50 |
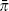 |
Inflation target | 0.00 |
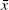 |
Long-run equilibrium of the output gap | 0.00 |
The structural changes we allow for are in either
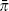 or
or
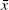 . If there are no breaks (Experiment 1)
these remain zero throughout. In the remaining experiments there is a break
in either the inflation target or potential output. When it is the former,
. If there are no breaks (Experiment 1)
these remain zero throughout. In the remaining experiments there is a break
in either the inflation target or potential output. When it is the former,
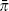 becomes 0.02 after 40 per cent of the sample
while, if it is the latter,
becomes 0.02 after 40 per cent of the sample
while, if it is the latter,
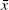 becomes −0.015 at that point
in the sample.
Experiment 2 is an exception. Here a break in the
inflation target occurs as above but we allow potential output to move from
zero to
becomes −0.015 at that point
in the sample.
Experiment 2 is an exception. Here a break in the
inflation target occurs as above but we allow potential output to move from
zero to 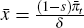 . This choice means
that the intercept in the NKPC,
c1, remains at zero, i.e. it does not show any breaks.
Experiments 3 and 4 look
at changing either the mean inflation rate,
. This choice means
that the intercept in the NKPC,
c1, remains at zero, i.e. it does not show any breaks.
Experiments 3 and 4 look
at changing either the mean inflation rate, 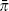 , or the mean of potential
output,
, or the mean of potential
output,
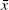 . Finally, Experiments 5
and 6 look at whether our conclusions depend on agents
correctly knowing the timing of any breaks. To assess this we consider the
case where agents believe that the means
. Finally, Experiments 5
and 6 look at whether our conclusions depend on agents
correctly knowing the timing of any breaks. To assess this we consider the
case where agents believe that the means 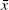 and
and
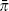 remain constant until 60 per cent of the sample is completed, whereas the actual
shift is at 40 per cent of the sample. As mentioned in Section 3
there are two ways of representing the decision rules of agents used in forming expectations.
One is to use the assumed (incorrect over part of the sample) model to produce
weights that can be applied to observables when forming expectations. This
is the ‘feedback’ form. The other is for agents to compute the
path that they believe the model variables would follow, and then use that
when forming expectations.
remain constant until 60 per cent of the sample is completed, whereas the actual
shift is at 40 per cent of the sample. As mentioned in Section 3
there are two ways of representing the decision rules of agents used in forming expectations.
One is to use the assumed (incorrect over part of the sample) model to produce
weights that can be applied to observables when forming expectations. This
is the ‘feedback’ form. The other is for agents to compute the
path that they believe the model variables would follow, and then use that
when forming expectations.
The parameter values above are standard. s was chosen to be 0.99 owing to the fact that in NKPCs s must equal or exceed the discount rate. In the model of Galí and Gertler (1999), when the discount rate is 0.99, the value of s varies between 0.99 and 0.996 – the variation comes from changing the probability of firms resetting prices, and the fraction of firms setting optimal prices, which can range from zero to one. This suggests that one might assume that s = 1 and then estimate a restricted estimator as per the unrestricted estimator but in which the true value of s is replaced by unity. We refer to this estimator as RES. This estimator will be biased in large samples since the error term will be augmented by the term (1−s)πt−1.
The six experiments were chosen to elucidate many of the issues mentioned in the introduction to the paper. When examining the results our focus will be on two things. First, even if there is no structural change, we can have a small-sample bias in the estimator of γ, simply because of weak instruments.[1] Second, when the intercept does shift, and no allowance is made for that, we have a specification error, which can cause a large-sample bias. One way to distinguish these two effects is to have breaks in means but none in the NKPC intercept, i.e. the breaks are offsetting as in Experiment 2. Then any bias must be due to weak instruments since the equation is correctly specified.
One way to detect weak instruments (infeasible in practice) is to compare the median and the mean of the estimators, since weak instruments mostly show up in the IV estimator not being normally distributed. Another way is to extend the sample and see if the bias goes away. Of course, in the case of the unrestricted estimator we only have one ‘free’ instrument, so that examining the F-test relating to the coefficient of rt−1 in the regression of πt+1 against xt, πt−1 and rt−1 will give good (feasible) information about weak instruments. The popular rule of thumb that F > 10 does in fact provide a reliable guide to those experiments where there are weak instruments. In interpreting the results below, it should be noted that structural change not only affects intercepts in equations like the Phillips curve but can also make instruments stronger or weaker due to changes in the reduced form. As mentioned earlier, we consider breaks that occur at 40 per cent of the sample size. But when agents have the timing of breaks wrong, they think breaks occur at 60 per cent of the sample. We use percentages as this enables us to increase the sample size to study the ‘asymptotic’ properties as well as the small-sample ones.
4.2 The Experiments
4.2.1 Experiment 1: no breaks
This experiment keeps all parameters constant while
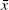 and
and
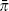 are both set to zero. Two sample sizes
are used,
T = 100 and T = 1,000, and 500 replications are performed
to assess estimator bias. The estimators are the unrestricted estimator (UE),
the restricted estimator that uses the correct sum of the forward and backward
parameters (RE), and the restricted estimator that just sets this sum to unity
(RES). We also estimate the sum of the coefficients with the unrestricted estimator.
Table 2 contains the results.
are both set to zero. Two sample sizes
are used,
T = 100 and T = 1,000, and 500 replications are performed
to assess estimator bias. The estimators are the unrestricted estimator (UE),
the restricted estimator that uses the correct sum of the forward and backward
parameters (RE), and the restricted estimator that just sets this sum to unity
(RES). We also estimate the sum of the coefficients with the unrestricted estimator.
Table 2 contains the results.
| T = 100 | T = 1,000 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| UE | RE | RES | UE | RE | RES | ||||
| γ | γ+α | γ | γ | γ | γ+α | γ | γ | ||
| Median | 0.59 | 1.05 | 0.35 | 0.39 | 0.36 | 1.00 | 0.30 | 0.35 | |
| Mean | 0.84 | 1.10 | 0.33 | 0.38 | 0.41 | 1.01 | 0.30 | 0.35 | |
| Note: True value of γ is 0.29 | |||||||||
The weak instrument bias shows up strongly in the unrestricted estimators. It is still present even when there are 1,000 observations; by 10,000 observations (results not shown) it has gone. The RES estimator always has a bias since, as we noted earlier, there is a missing regressor (1−s)πt−1 that enters the error term. When there are 10,000 observations, the mean and median of the RES estimator of γ are 0.34 which seems to be the asymptotic bias. The general impression from Table 2 is that for typical sample sizes (i.e. 25 years of quarterly data) it would be worth using RES rather than UE, despite its large-sample bias. It is close to being normally distributed and the bias is reasonably small. In practice, many people have imposed the restriction that s = 1 in estimation, and the bias could be lower than shown here as we have replaced the true s = 0.99 with an assumed value of s = 1, whereas a discount factor of 0.99 would imply that the true value of s lies much closer to unity than we have assumed in this experiment. Since the bias depends directly on the difference between the assumed and true values it can be much smaller if these are close.
4.2.2 Experiment 2: breaks in means but not in the intercept of the NKPC
Here we allow
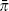 to break, going to 0.02 per quarter
from zero, but choose
to break, going to 0.02 per quarter
from zero, but choose
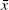 so that the intercept in the Phillips
curve remains constant. Hence there is no specification bias in the UE and
RE estimators. All other parameters are as in Experiment 1. As the standard
deviation of inflation in the model is 0.003 this is an enormous break and
is chosen to maximise the effects. Table 3 shows that the UE estimator now
has a relatively small bias and is close to being normally
distributed.[2]
This is due to the instruments becoming far better due to the break in the inflation
process. Indeed, this is confirmed when we allow for a much smaller break
of 0.005. Then the median and mean of γ
in the UE case become 0.39 and −0.08 when T = 100, while the
RES estimator does not change.
By T = 1,000, however, the UE estimator seems reasonably well
behaved. If the evidence is that the instruments are good, it would suggest
that one use UE, but otherwise the RES estimator does not seem to be badly
biased, even in small samples, and is probably preferred.
so that the intercept in the Phillips
curve remains constant. Hence there is no specification bias in the UE and
RE estimators. All other parameters are as in Experiment 1. As the standard
deviation of inflation in the model is 0.003 this is an enormous break and
is chosen to maximise the effects. Table 3 shows that the UE estimator now
has a relatively small bias and is close to being normally
distributed.[2]
This is due to the instruments becoming far better due to the break in the inflation
process. Indeed, this is confirmed when we allow for a much smaller break
of 0.005. Then the median and mean of γ
in the UE case become 0.39 and −0.08 when T = 100, while the
RES estimator does not change.
By T = 1,000, however, the UE estimator seems reasonably well
behaved. If the evidence is that the instruments are good, it would suggest
that one use UE, but otherwise the RES estimator does not seem to be badly
biased, even in small samples, and is probably preferred.
| T = 100 | T = 1,000 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| UE | RE | RES | UE | RE | RES | ||||
| γ | γ+α | γ | γ | γ | γ+α | γ | γ | ||
| Median | 0.32 | 0.99 | 0.34 | 0.37 | 0.30 | 0.99 | 0.31 | 0.34 | |
| Mean | 0.37 | 0.98 | 0.32 | 0.36 | 0.30 | 0.99 | 0.31 | 0.36 | |
| Note: True value of γ is 0.29 | |||||||||
4.2.3 Experiment 3:
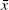 breaks, intercept in NKPC shifts
breaks, intercept in NKPC shifts
This experiment is like the preceding one but
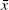 is assumed not to change. It should
be noted that even though the break in
is assumed not to change. It should
be noted that even though the break in
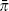 is large (0.02) this does not lead
to a large break in the NKPC intercept, as the latter is (1 − s)
is large (0.02) this does not lead
to a large break in the NKPC intercept, as the latter is (1 − s)
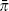 t. Table 4 gives the results.
There do seem to be some weak instrument issues with the UE estimator but the
striking result is that the bias in γ is downward,
showing that breaks in the NKPC intercept cannot always be assumed to lead
to an upward bias. The restricted estimators are now more biased than before,
but RES still seems a reasonable estimator to employ when the alternative is
the UE estimator. It is noticeable that s = γ + α
is quite well estimated here, so the downward bias in the estimator of γ
is offset by an upward bias in the estimator of α.
t. Table 4 gives the results.
There do seem to be some weak instrument issues with the UE estimator but the
striking result is that the bias in γ is downward,
showing that breaks in the NKPC intercept cannot always be assumed to lead
to an upward bias. The restricted estimators are now more biased than before,
but RES still seems a reasonable estimator to employ when the alternative is
the UE estimator. It is noticeable that s = γ + α
is quite well estimated here, so the downward bias in the estimator of γ
is offset by an upward bias in the estimator of α.
| T = 100 | T = 1,000 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| UE | RE | RES | UE | RE | RES | ||||
| γ | γ+α | γ | γ | γ | γ+α | γ | γ | ||
| Median | 0.26 | 0.98 | 0.34 | 0.38 | 0.20 | 0.97 | 0.33 | 0.38 | |
| Mean | 0.35 | 0.99 | 0.34 | 0.39 | 0.16 | 0.97 | 0.33 | 0.38 | |
| Note: True value of γ is 0.29 | |||||||||
4.2.4 Experiment 4:
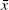 breaks, intercept in NKPC shifts
breaks, intercept in NKPC shifts
The size of the break in
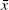 for this experiment is −0.015.
Again this is some five times the standard deviation and so is very large.
Because it is not multiplied by the term (1−s) in the NKPC intercept
(as
for this experiment is −0.015.
Again this is some five times the standard deviation and so is very large.
Because it is not multiplied by the term (1−s) in the NKPC intercept
(as
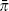 was) it produces large changes in the
latter. Table 5 gives the results. Instruments are obviously much better so
the distributions look normal, although there is a major specification bias.
The specification error does result in an upward bias to the UE estimator of
γ, as was observed by Castle et al (2010)
and Russell
et al (2010), although it is not due to shifting means in
the inflation process. Even if the shift is just −0.005, the UE estimates
of the mean and median of γ remain at 0.5 (T = 100),
while the RES estimates are 0.43, making them much more robust against moderate
breaks, and one retains the impression from previous experiments that it would
be a preferred estimator.
was) it produces large changes in the
latter. Table 5 gives the results. Instruments are obviously much better so
the distributions look normal, although there is a major specification bias.
The specification error does result in an upward bias to the UE estimator of
γ, as was observed by Castle et al (2010)
and Russell
et al (2010), although it is not due to shifting means in
the inflation process. Even if the shift is just −0.005, the UE estimates
of the mean and median of γ remain at 0.5 (T = 100),
while the RES estimates are 0.43, making them much more robust against moderate
breaks, and one retains the impression from previous experiments that it would
be a preferred estimator.
| T = 100 | T = 1,000 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| UE | RE | RES | UE | RE | RES | ||||
| γ | γ+α | γ | γ | γ | γ+α | γ | γ | ||
| Median | 0.51 | 1.03 | 0.47 | 0.47 | 0.51 | 1.03 | 0.47 | 0.47 | |
| Mean | 0.51 | 1.13 | 0.46 | 0.47 | 0.51 | 1.03 | 0.46 | 0.47 | |
| Note: True value of γ is 0.29 | |||||||||
4.2.5 Experiment 5: as Experiment 3 but agents think the break is at 60 per cent of the sample
By comparing Tables 4 and 6 it is clear that the properties of the estimators are basically the same, even though agents get the timing of the structural break incorrect.
| T = 100 | T = 1,000 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| UE | RE | RES | UE | RE | RES | ||||
| γ | γ+α | γ | γ | γ | γ+α | γ | γ | ||
| Median | 0.26 | 0.98 | 0.34 | 0.38 | 0.21 | 0.98 | 0.33 | 0.37 | |
| Mean | 0.22 | 0.97 | 0.34 | 0.38 | 0.19 | 0.97 | 0.32 | 0.37 | |
| Note: True value of γ is 0.29 | |||||||||
4.2.6 Experiment 6: as Experiment 3, agents still think the break is at 60 per cent of the sample but expectations are based on path computation
We only show results for a large sample (Table 7). Compared to either Tables 4 or 6, the pathway of forming expectations produces a very large downward bias in the estimates of γ for the UE. With 10,000 observations, the median of the UE is −1.27 and the mean −1.67, while the two restricted estimators stay at 0.41 and 0.47. By 100 observations, the UE median and mean become −1.24 and −1.30, so the generation of expectations increases the bias a great deal in the UE but not for the RE. Again the sum is much better estimated.
| T = 1,000 | ||||
|---|---|---|---|---|
| UE | RE | RES | ||
| γ | γ+α | γ | γ | |
| Median | −0.25 | 0.97 | 0.41 | 0.46 |
| Mean | −1.29 | 0.93 | 0.41 | 0.46 |
| Note: True value of γ is 0.29 | ||||
This experiment makes the point that, if agents ignore observable evidence that their past expectations were wrong, one could see major biases in the NKPC. In the previous experiment, agents did not ignore this evidence. Their expectations were model consistent but to the wrong model (at least until 60 per cent of the sample was complete), but the feedback form they use for expectations does reflect the structural changes that took place, i.e. it shows up in zt−1. Hence, agents in Experiment 5 are effectively learning about the structural change from the viewpoint of expectations formation.
Footnotes
In fact the bias can exist for very large samples, even though it disappears asymptotically. [1]
The distribution of the IV estimator is often non-normal in the presence of weak instruments. As non-normality implies a difference between the mean and median of the estimator a simple way to detect weak instruments (not available in practice) is to compare these two moments. [2]