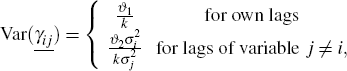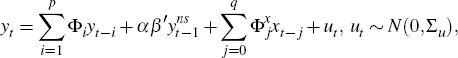RDP 2013-07: An Empirical BVAR-DSGE Model of the Australian Economy 3. Estimating the Models
June 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 658KB
3.1 Estimating the DSGE Model
We estimate the DSGE model outlined above in two stages. The first stage is to estimate a BVAR model of the foreign sector with Minnesota priors using aggregates of foreign variables. This is a legitimate strategy if it is assumed that the foreign economy is predetermined and exogenous to the small economy (Jääskelä and Nimark 2011). The estimates may not be efficient if there are restrictions on the parameters across the economies included in the aggregates, but will be consistent. Second, we take the results from this BVAR model to calibrate the foreign sector in the DSGE model, and estimate the domestic parameters.
3.1.1 Estimating the large economy Minnesota VAR
We estimate a BVAR for the foreign sector closely following Kadiyala and Karlsson (1997), using the following variables:
- detrended level of output of Australia's trading partners
- trade-weighted inflation
- a G7 PPP-weighted interest rate
- detrended level of the terms of trade.
We use broad aggregates for output and inflation in an attempt to partially capture the increasing importance of China in the world economy, which is of particular relevance for Australia as a net exporter of commodities. Further details about the data are given in Appendix C.
We use univariate first-order autoregressive priors. These Minnesota priors are commonly used in forecasting. The parameters in each equation are assumed to follow a multivariate normal distribution. As we assume that these series are stationary, the Minnesota prior would usually set the means of the prior distributions to be zero, including those on the first lag. In an attempt to improve forecasting performance, we estimate first- and higher-order autoregressive processes for each series, over the sample 1982:Q3–1992:Q4. Based on these autoregressions, we set the prior on the own first lag parameter to be 0.7 and 0.4 for output and inflation, and 0.8 for the interest rate and the terms of trade. The mean of the prior for all other coefficients is set to zero, and we ensure that the prior is held more tightly for parameters on longer lags and on lags of non-dependent variables.
The variance of the prior is governed by two parameters, ϑ1 and ϑ2, for coefficients on own lags and other coefficients respectively. The variance of the prior for the coefficient on the jth variable in the ith equation of the large economy VAR, where underbars denote that the parameters are priors, is set following Kadiyala and Karlsson (1997) as:
where k is the lag length and σi is the standard error from an autoregression of the same order as the VAR for the ith variable. To select ϑ1 and ϑ2, we examine the forecasting performance of the model over the pre-sample period 1989:Q4–1992:Q4. We select ϑ1 = 0.01 and ϑ2 = 0.003; if more weight is placed on the one-quarter-ahead forecasts than year-ahead forecasts, a slightly tighter prior would be chosen. Subsequently, this VAR is used to generate our large economy forecasts.
3.1.2 DSGE calibration
In the second step we use the parameter estimates from the Minnesota VAR described above as the large economy parameters of the DSGE model and calibrate the parameters of the DSGE model that enter the steady state (with one exception).[6] The remaining parameters are estimated using Bayesian methods in Dynare. The observed variables are described in Section 3.4.
The calibrated parameter values are shown in Table 1. The discount factor, β, is chosen to imply a steady state annual interest rate of 3 per cent. The inverse Frisch elasticity of substitution is set to 1, approximately the median estimated by Justiniano and Preston (2010b). The value governing the sensitivity of domestic interest rates to foreign debt is also taken from Justiniano and Preston (2010b). The elasticity of substitution between individual domestically produced and imported goods is set to imply a steady state mark-up of 25 per cent, following Cagliarini, Robinson and Tran (2011).
| Coefficient | Description | Value |
|---|---|---|
| β | Discount factor | 0.9925 |
| Ψ | Inverse Frisch elasticity | 1 |
| χ | Interest debt sensitivity | 0.01 |
| γ | Weight on domestic good in consumption | 0.65 |
| σ | Elasticity of substitution: domestic and imported goods | 1.5 |
| λm | Elasticity of substitution: individual imported goods | 4 |
| λ | Elasticity of substitution: individual domestic goods | 4 |
| ξ | Elasticity of substitution of labour between sectors | 0.75 |
| δ1 | Depreciation rate, domestic goods | 0.018 |
| δ2 | Depreciation rate, commodity sector | 0.012 |
| α1 | Weight on capital in domestic goods production | 0.3 |
| α2 | Weight on capital in commodity production | 0.77 |
There is little literature on the mobility of labour between sectors in response to real wage differentials in Australia, and as we estimate the model without using labour market data we set ξ = 0.75.[7] The depreciation rates are chosen with reference to annual national accounts data, which suggest that the depreciation rate in the mining sector is lower than in the rest of the economy at nearly 5 per cent per annum. Capital's share of mining sector income, α2, is selected using the values reported in the experimental multifactor productivity estimates from the Australian Bureau of Statistics (ABS).
The one parameter entering the steady-state that we estimate is υ, the intensity of external habits. We do this as different papers have very different estimates; for example, Jääskelä and Nimark (2011) obtain a posterior mean of 0.76, whereas the median value from Justiniano and Preston (2010b) is 0.33. Consequently we set the mean of the prior to be 0.5.
Using the parameter values discussed above, and the mean of the prior for υ, we calibrate the remaining parameters γ, σ and α1 so that the implied ratios of nominal consumption, investment, imports and compensation of employees to value-added output are approximately average of the sample 1993:Q1–2011:Q2 (Table 2). The consumption to value-added output ratio is particularly sensitive to σ, and a low value is necessary to match the data. The capital intensity of the domestic good sector influences the compensation of employees to value-added output ratio; setting α1 to 0.3 means that it is considerably more labour intensive than the commodity sector, where α2 is set to 0.77.
| Nominal ratio to value added | Data | Model |
|---|---|---|
| Consumption | 0.748 | 0.724 |
| Non-residential investment | 0.258 | 0.210 |
| Compensation of employees | 0.492 | 0.477 |
| Imports | 0.203 | 0.219 |
|
Note: ‘Consumption’ is all sectors Sources: ABS; authors' calculations |
||
The priors for the parameters that do not enter the steady state are selected as follows. For the Phillips curves, our prior is that values higher than those implied by microeconomic data for both the Calvo parameter and indexation will be necessary to provide a realistic description of the behaviour of aggregate inflation (for further discussion on this see Cagliarini et al (2011)). The values selected for the Taylor rule are mostly standard and similar to those in Justiniano and Preston (2010b), although we place a slightly larger prior on growth in the Taylor rule since, in some DSGE models (including Justiniano and Preston (2010b)), this has been estimated to be more important than the response to the log-linearised level of output.[8]
We allow for autocorrelation in the growth rate of technology. However, as little persistence is evident in Australian output growth, we select a loose prior, to accommodate the possibility that it is low. For the other shocks, our prior on the autoregressive coefficients are similar to Justiniano and Preston (2010b). The adjustment cost parameter prior is based on Smets and Wouters (2007).
Turning to the standard deviations of the shocks, we set the mean of the prior for a quarterly monetary policy shock to be 25 basis points. Relatively large values are used for the standard deviation of technology shocks in the export sector and, in particular, the investment productivity shocks, reflecting the fact that growth in these expenditure aggregates are more volatile than aggregate GDP.
3.1.3 DSGE posterior
We used random-walk Metropolis-Hastings chains with 400,000 observations to find the posterior densities, dropping the first 80 per cent of these observations.[9] Table 3 below shows some characteristics of the posterior densities from the sample 1993:Q1–2011:Q2.
| Coefficient | Description | Prior | Posterior | ||||
|---|---|---|---|---|---|---|---|
| Density | Mean | Std dev | Mean | 90% HPD | |||
| θ1 | Calvo domestic prices | B | 0.75 | 0.1 | 0.95 | 0.94–0.97 | |
| ω1 | Indexation, domestic | B | 0.3 | 0.05 | 0.33 | 0.25–0.40 | |
| ζR | Taylor rule, smoothing | B | 0.5 | 0.1 | 0.82 | 0.77–0.87 | |
| ζπ | Taylor rule, inflation | N | 1.5 | 0.1 | 1.48 | 1.31–1.64 | |
| ζνa | Taylor rule, output | B | 0.5 | 0.2 | 0.72 | 0.53–0.90 | |
| ζdy | Taylor rule, growth | B | 0.5 | 0.2 | 0.16 | 0.02–0.29 | |
| θm | Calvo import | B | 0.75 | 0.1 | 0.89 | 0.83–0.96 | |
| ωm | Indexation, imports | B | 0.3 | 0.05 | 0.31 | 0.23–0.39 | |
| ρα | Technology growth | B | 0.5 | 0.2 | 0.33 | 0.12–0.55 | |
| ρrp | Risk premium | B | 0.75 | 0.1 | 0.92 | 0.88–0.96 | |
| ρi | Investment technology | B | 0.75 | 0.1 | 0.51 | 0.38–0.64 | |
| ρa,2 | Export technology | B | 0.75 | 0.1 | 0.79 | 0.68–0.90 | |
| ρg | Preferences | B | 0.75 | 0.1 | 0.75 | 0.65–0.85 | |
| η″ | Adjustment costs | N | 4 | 1 | 1.48 | 0.72–2.27 | |
| υ | Habits | B | 0.5 | 0.1 | 0.34 | 0.23–0.45 | |
| Standard deviations | |||||||
| σrp | Risk premium | IG | 1 | 1 | 0.46 | 0.31–0.59 | |
| σM | Monetary policy | IG | 0.25 | 0.1 | 0.10 | 0.08–0.12 | |
| σa | Technology | IG | 1 | 1 | 0.46 | 0.32–0.59 | |
| σ2 | Export technology | IG | 2 | 1 | 2.21 | 1.91–2.51 | |
| σi | Investment technology | IG | 5 | 1 | 6.52 | 3.79–9.37 | |
| σc | Preferences | IG | 1 | 1 | 3.37 | 2.46–4.20 | |
| σ1 | Domestic mark-up | IG | 0.5 | 1 | 0.16 | 0.13–0.18 | |
| σm | Imports mark-up | IG | 0.5 | 1 | 0.33 | 0.13–0.54 | |
| Notes: Prior distributions are B – Beta, N – Normal, IG – inverse Gamma; HPD denotes highest probability density; foreign sector estimates are excluded from this table | |||||||
There are several aspects of the posterior estimates to note. First, the mean Calvo parameter for domestically produced goods is very high (0.95), and the posterior is very tight. Taken literally, this implies price adjustment occurs very infrequently, and is at odds with microeconomic pricing data. It is, however, similar to estimates based on the generalised method of moments (GMM) (e.g. Kuttner and Robinson 2010), but much higher than the DSGE-based estimates from Robinson (2013), although the latter probably are artificially low due to the way that model is mapped to the data.[10] Such a high value implies a very flat Phillips curve, and consequently monetary policy shocks, while having substantial real effects, have only a small impact on inflation. We present analysis later that examines the sensitivity of the results to this parameter being calibrated to the mean of its prior. The estimates of the indexation parameters do not differ considerably from their priors.[11]
Turning to the Taylor rule, policy is estimated to be much less aggressive towards inflation than was found by Robinson (2013) and remains close to the prior. Policy is more responsive to the deviation of the level of output from its steady state than to output growth (considerably more than was found by Justiniano and Preston (2010b)).[12] A one standard deviation quarterly monetary policy shock is found to be around 10 basis points.
Considering investment, the mean adjustment cost parameter is lower than our prior. We experimented with allowing separate capital technology shocks and adjustment cost parameters for the export sector. It is plausible that these have separate effects, given that the investment boom currently underway in the mining sector has not been reflected in export volumes to a commensurate degree, reflecting the long time it takes for mining investment to become operational and production being disrupted as capacity is expanded. Unfortunately, neither could be identified, which may reflect the fact that aggregate, rather than sectoral, investment data is being used, and therefore both were excluded. Also, it may be difficult to disentangle a sectoral technology shock from a sectoral investment-specific shock.
3.2 Estimating the BVAR-DSGE
We now turn to the form of the BVAR-DSGE model that we wish to estimate and use for forecasting. The large economy variables are included as exogenous variables in the equations for the small open economy. We do this because central banks will typically have detailed information about their domestic economy, but fewer resources to monitor other countries. They might use forecasts from international organisations (e.g. the International Monetary Fund's (IMF) World Economic Outlook and the Organisation for Economic Co-operation and Development's (OECD) Economic Outlook) or Consensus Economics, which survey market economists, in addition to those compiled internally. Note that if these non-VAR forecasts for the large economy were used it is still necessary to incorporate a model for the large economy variables in the DSGE model.
The form of the BVAR with exogenous variables (BVARX) model we estimate is:
where yt is a vector of n small economy variables that
can be split into two components, namely 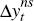 which are the first
difference of variables that according to the DSGE model are non-stationary,
and
which are the first
difference of variables that according to the DSGE model are non-stationary,
and 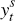 ,
which are stationary. Φi are coefficients on lags of
yt,
,
which are stationary. Φi are coefficients on lags of
yt, 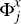 are the coefficients on the contemporaneous
terms and lags of xt, which is a vector of the large economy
variables, and ut are the shocks, which are normally distributed
with variance-covariance matrix
Σu.[13]
Because the DSGE model contains a permanent technology shock, it predicts cointegration
among the non-stationary observed variables. As in Del Negro et al
(2007), we estimate a vector error correction model, where β
is the cointegrating vector (we impose the values estimated from the DSGE model)
and α are the loadings on the error-correction terms. We will
refer to this model as a BVECMX
model.[14]
We also estimate a variant without these cointegrating terms, namely a BVARX
model.
are the coefficients on the contemporaneous
terms and lags of xt, which is a vector of the large economy
variables, and ut are the shocks, which are normally distributed
with variance-covariance matrix
Σu.[13]
Because the DSGE model contains a permanent technology shock, it predicts cointegration
among the non-stationary observed variables. As in Del Negro et al
(2007), we estimate a vector error correction model, where β
is the cointegrating vector (we impose the values estimated from the DSGE model)
and α are the loadings on the error-correction terms. We will
refer to this model as a BVECMX
model.[14]
We also estimate a variant without these cointegrating terms, namely a BVARX
model.
3.2.1 The BVECMX prior
The approach we take to construct the prior follows Robinson (2013), which itself draws on DeJong, Ingram and Whiteman (1993). In brief, by repeatedly drawing DSGE parameters from their posterior, simulating data using these parameters, and estimating a VAR on the simulated data, we map out what the DSGE posterior implies for the BVECMX parameters and the variance-covariance matrix of the shocks. We then use these estimates to inform our selection of the parameters of the prior. We assume that the parameters are distributed according to the independent Normal-Wishart prior described by Koop and Korobilis (2010), and restrict the parameter space to where the VAR is stable.[15] This prior allows different equations to include different variables and consequently accommodates block exogeneity. While this is not relevant when estimating a BVECMX model, the prior can accommodate the Minnesota prior and its small open economy variant, which we use as a benchmark. Finally, one way of relaxing the prior on the BVECMX parameters is to scale up its variance-covariance matrix by a factor of λ, which implies that the prior is given less weight in the estimation of the BVECMX.[16]
3.2.2 The BVECMX posterior
The joint posterior of the BVECMX parameters and the inverse of the variance-covariance matrix do not have a convenient form. However, the posterior distribution of the BVECMX parameters, conditional on the inverse of the variance-covariance matrix, and vice-versa, do have a convenient form. This enables us to use Gibbs sampling to produce realisations from the posterior.[17] The details of these distributions are given in Robinson (2013); the stability condition truncates these to the region where the VAR is stable.[18]
3.3 Estimating the Benchmark Models
Two types of benchmark model are estimated to produce comparison forecasts for the BVECMX in addition to the DSGE model, namely a small open economy (SOE) Minnesota VAR and separate univariate AR(2) models for each observed variable. The latter are estimated using maximum likelihood. We also combine the point forecasts from the DSGE model with those from the SOE Minnesota VAR using equal weights as another benchmark.[19]
3.3.1 The small open economy Minnesota VAR
In the SOE Minnesota VAR, the large economy variables are included in the vector of endogenous variables and block exogeneity is imposed. Unlike the large economy Minnesota VAR used as a prior for the BVECMX, we do not treat the variance-covariance matrix of the shocks as fixed; instead, we use the variant of the independent Normal-Wishart prior described above. Consequently, the SOE Minnesota VAR is a natural benchmark for the BVECMX model.
The main way the SOE Minnesota VAR differs from the BVECMX model is in the parameters of the prior. For the large economy equations, the priors are the same and block exogeneity is imposed. For the small economy equations we estimate first-order and higher-order autoregressive models, as was done for the large economy Minnesota VAR above, with the longest pre-sample used being 1982:Q3–1992:Q4.[20] Based on these, we set the mean of the prior for the coefficient on the first lags to be:
- exports: 0
- investment: 0
- output: 0.3
- inflation: 0.6
- interest rates: 0.7
- real exchange rate: 0.0.
The remaining parameters of the prior for the SOE Minnesota VAR are ϑ1 and ϑ2, which determine the standard deviations of the prior on the coefficients on lags of the own variable and other variables. As for the large economy Minnesota VAR, to choose these we examined the performance of a Minnesota VAR in forecasting the Australian variables over a pre-sample period 1989:Q4–1992:Q4.[21] We set ϑ1 = 0.07; there appeared to be a trade-off between the one-quarter-ahead (which would suggest a smaller value for ϑ1) and the year-ahead forecasts. The forecasting exercise suggested a very small value of ϑ2, which would effectively reduce the VAR to a collection of univariate autoregressive processes. Consequently we set ϑ2 = 0.005, which Kadiyala and Karlsson (1997) describe as a standard value. We construct the prior for the variance-covariance matrix of the shocks so that the mean coincides with that of the Minnesota prior, following Kadiyala and Karlsson.[22]
3.4 Data
The endogenous and exogenous variables we include in the BVECMX are also the variables used in the estimation of the DSGE model. The 10 observed variables are:
- detrended trade-weighted output
- trade-weighted inflation
- a G7 interest rate
- detrended terms of trade
- exports growth
- investment growth
- non-farm output growth
- underlying inflation
- the cash rate
- the change in the real trade-weighted exchange rate.[23]
Details of the data are given in Appendix C.[24]
The observed real exchange rate is defined such that an appreciation is an increase and the terms of trade is the ratio of export to import prices; both definitions are the norm for Australia. The former is the inverse of that in the model, and the measurement equation is adjusted accordingly. The longest estimation sample in the forecasting exercise is 1993:Q1–2011:Q1.[25]
Footnotes
Pre-estimating the large economy does restrict the data that can be used to estimate the DSGE model. In particular, the (stationary) level of foreign output and terms of trade are of importance for the small economy. If the VAR is estimated in first differences, the DSGE with it imposed would not have a solution, and therefore we detrend these series. [6]
Drawing on the estimates of Iacoviello and Neri (2010) for the United States. [7]
We do not allow a role for the exchange rate in the Taylor rule, reflecting the findings of Lubik and Schorfheide (2007). The exchange rate may still be of importance to policy, but through its impact on inflation and output, rather than directly. [8]
Two chains were run in order to check for convergence. For the forecasting exercise, a single chain for each period was used. [9]
In particular, in Justiniano and Preston (2010a), import prices in the terms of trade are matched to retail prices, whereas in the Australian data import prices are measured ‘at the dock’, without any retail mark-up. [10]
We experimented with allowing autocorrelation in the mark-up shocks. However, for domestic prices the autocorrelation coefficient tended to be very small and for import prices it appeared not to be identified. Consequently, autocorrelation is excluded for both. [11]
To some extent this might reflect that we have allowed technology to be non-stationary, whereas they linearly detrend observed output. [12]
For simplicity we set p = q. [13]
In the DSGE model, variables such as exports, investment and output are stationary
when normalised by technology, for example, 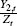 and
and 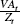 .
Consequently
.
Consequently 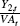 also is stationary, and therefore the log
of exports and output are cointegrated with coefficients 1 and −1.
[14]
also is stationary, and therefore the log
of exports and output are cointegrated with coefficients 1 and −1.
[14]
This places a multivariate normal prior over the (vectorised) parameters of the VAR, and a Wishart prior over the inverse of the variance-covariance matrix of the reduced-form shocks. We set the degrees of freedom parameter in the latter to be n+2. [15]
As the number of parameters in the BVECX is greater than that in the DSGE, to ensure that the prior for the variance-covariance matrix of the parameters is non-singular we add a small amount (0.01) to the standard deviation for all parameters. This is added after any scaling by λ. [16]
We simulate 31,000 observations, dropping the first 1,000. [17]
This is implemented by dropping all unstable draws. [18]
More sophisticated approaches could have been used, such as those in Bache et al (2011) or Geweke and Amisano (2011), although equal weights have been found in the past to perform well (for example, Clemen (1989)). [19]
For investment, the sample was 1986:Q1 onwards due to data availability. [20]
We use the Minnesota prior to save computational time, and exclude business investment due to data availability. [21]
As before, we set the degrees of freedom parameter in the Wishart distribution to be n+2. [22]
There are 10 observable variables in the DSGE model, but 12 structural shocks. If one were to identify the model, rather than focus on forecasting, then setting the number of observable variables equal to the number of structural shocks may be preferable. [23]
All series are demeaned before estimation. The detrending was done with a Hodrick-Prescott filter with the smoothing parameter set equal to 1,600. [24]
The variables are included in the order listed. [25]