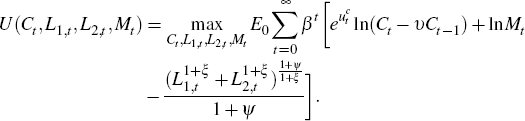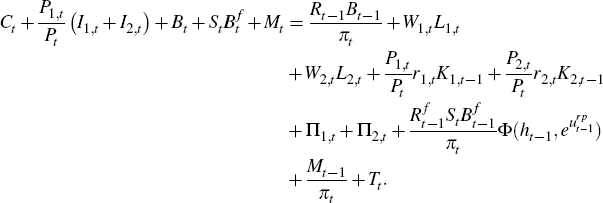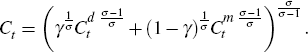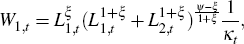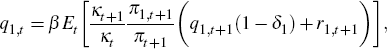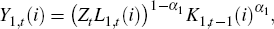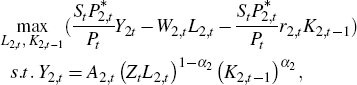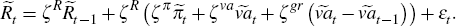RDP 2013-07: An Empirical BVAR-DSGE Model of the Australian Economy 2. The DSGE Model

This section describes the DSGE model that we later use as a forecasting benchmark and as a prior for the empirical BVAR. We begin by describing the domestic economy, with particular emphasis on departures from the standard small open economy framework that allow us to introduce a separate commodity sector.

2.1 The Domestic Economy

The domestic economy in the DSGE model differs from the standard small open economy framework by the inclusion of a second source of production, which we add to represent the commodity sector. The result of this addition is that the terms of trade are exogenous, and there are sector-specific expressions for labour supply and investment. We describe each agent's problem, but focus primarily on the non-standard aspects. The log-linearised and steady state equations are in Appendices A and B. A subscript of 1 denotes the domestic good sector, a subscript of 2 the commodity sector, which produces for export.

2.1.1 Consumers

The representative consumer derives utility from consuming C_t and holding real money balances M_t, and disutility from working. One departure from the standard literature is that the hours worked are divided between the domestic and export good sectors, L_1,t and L_2,t respectively. We assume that these are imperfect substitutes, and therefore that wages can differ across the sectors. The consumer also derives income from renting capital to both sectors, r_1,t and r_2,t, dividends from monopolistically competitive firms, π_1,t and π_2,t, holdings of domestic and foreign one-period risk-free bonds, B_t and 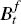, which earn R_t and 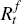, and transfer payments, T_t. Utility is defined to be:

Consumers face a budget constraint, expressed in real terms as:

P_t is the price of the final consumption good and I_i,t denotes investment. Foreign borrowing is done at a premium on domestic bond returns determined by a function Φ, which depends on the level of net foreign assets as a share of GDP, h_t, and a risk premium shock 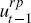. π_t is consumer price inflation, S_t the nominal exchange rate (A$ per unit of foreign currency), W_i,t are real wages (deflated by consumer prices) and K_i,t the capital stock with gross rental rate r_i,t. 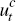is a preference shock; β is the discount factor; υ is the strength of external habits; ψ is the inverse Frisch elasticity and ξ governs the substitutability of labour between the sectors.^[3] An expression for the evolution of nominal net foreign assets as a share of GDP, h, can be obtained by manipulating this budget constraint.

The capital stock evolves in the same way in each sector, although depreciation rates differ. Investment adjustment costs are included, following Smets and Wouters (2007), and there is an investment-specific shock that is common across sectors.

The consumption good is a constant elasticity of substitution (CES) aggregate of domestically produced goods from sector 1 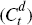and imports 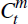, where σ is the elasticity of substitution between goods and γ governs the relative importance of domestically produced goods in the consumption basket:

The first order conditions of the consumer's problem leads to a standard Euler equation and an uncovered interest rate parity condition. The non-standard features are the labour supply conditions. For example, for the domestic good sector, the labour supply equation is determined by

where κ_t is the Lagrange multiplier for the budget constraint. An analogous condition applies to the export sector. The allocation of hours worked across the sectors will depend on relative wages. The sensitivity of labour supply to wage differentials is determined by ξ. The marginal utility from investing in a further unit of capital relative to consumption, Tobin's Q, is defined for each sector as the ratio of the Lagrange multiplier on the capital accumulation equation for a sector to that on the budget constraint. We express Tobin's Q in terms of consumer prices for the domestic good sector as:

where π_1,t is inflation in the domestic good sector. The depreciation and rental rates of capital, δ_i and r_i, and the Euler equations are sector-specific.

2.1.2 Domestic good sector

Domestic good sector firms rent capital and hire labour from households, and use a Cobb-Douglas production function. α₁ governs how capital intensive domestic good production is, and it is assumed to be less than the corresponding parameter in the relatively capital intensive commodity sector. There is a unit continuum of firms; for the ith firm:

where Y_1t(i) is output and Z_t is labour-augmenting technology. We assume that Z_t follows a unit root without drift, and allow for autocorrelation in its growth rate.^[4] A consequence of this is that most real variables will follow the same trend and be cointegrated with output. If we had allowed for drift then the level of most real variables would also share a common linear trend; we relax this assumption in estimation by demeaning the observed variables (which for output, investment and exports will be achieved by using growth rates). The domestic good sector firm determines its demand for capital (K_1,t−1(i)) and labour (L_1,t(i)) by minimising real cost, deflated by the price of their output, taking W_1t and r_1t as given.

The output from the domestic good sector is sold to a domestic good aggregator, that aggregates it using CES technology, with a time-varying parameter .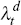

Cost minimisation by the domestic aggregator leads to a demand curve for individual goods, which the producers take as given. The domestic good sector is imperfectly competitive, and there is stickiness in prices, generated by Calvo pricing, whereby there is a fixed probability that a firm can reset its price each period. When log-linearised, this gives rise to a standard New-Keynesian Phillips curve for π_1,t. We allow for rule-of-thumb pricing, following Galí and Gertler (1999), such that a fraction of firms that are able to reset their prices do not do so optimally, but use a simple rule based on past inflation. The variable elasticity of substitution 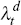introduces a mark-up shock to the Phillips curve.

2.1.3 Export sector

The model for the export sector draws on Dib (2008). It is perfectly competitive, and takes the world price for exports (commodity prices in foreign 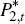currency), , as given, and in domestic currency 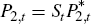. The world price is distinct from foreign consumer prices, 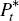. The exporter's problem in real terms (deflated by consumer prices) is:

where A_2,t is an export-specific technology shock. While we calibrate the export firms to match the Australian mining sector, for simplicity we have not allowed for decreasing returns to scale, even though this may be a better characterisation of the natural resource sector. Consequently, these effects may be captured by the productivity shock (or to some extent the investment shock), together with the investment adjustment costs. The assumption that the export sector is perfectly competitive, and hence a price taker, for Australia is also questionable, as it is a major exporter of both iron ore and coking coal and may have some pricing power in these markets, but we leave exploring alternative pricing assumptions to future research.

2.1.4 Importing firms

The importing sector is standard and is similar to that in Monacelli (2005). The law-of-one-price is assumed to hold at the docks, and the importer purchases a bundle of goods at price 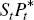. They then costlessly differentiate these goods and, as the sector is monopolistically competitive, the retail price faced by the consumer is a mark-up on real marginal costs, namely 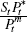. There is Calvo pricing in import prices, and consequently we obtain a New-Keynesian Phillips curve. Analogous to the domestic good aggregator, we allow the elasticity of substitution to vary, which introduces an exogenous mark-up shock into the Phillips curve. The aggregation of the import goods into the bundle 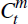can be done by either a perfectly competitive firm using CES technology or the consumer. Note that the terms of trade, namely the ratio of export prices to import prices at the docks, is 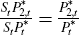, which corresponds to real commodity prices and is exogenous to the small economy.

2.1.5 Monetary policy

The central bank sets the policy rate using a Taylor rule, in which it reacts to the past interest rate, the log-linearised level (˜ denotes log-deviations from steady state) of inflation and value-added output, va_t, as well as growth in value-added output.^[5] The rule is:

2.1.6 Market-clearing conditions

Apart from factor markets, the market-clearing conditions for the ith domestic good firm is that its output equals that demanded by the aggregator. Identical conditions hold for importers. The market-clearing condition for the domestic good aggregator is:

Aggregated output from the domestic good producers can be consumed or invested. The assumptions that exports are comprised of commodities alone and all capital goods are produced domestically are strong ones. Capital goods are a substantial proportion of imports in the data, and the model will be unable to capture the downward relative price trend of capital imports relative to consumption goods, which is in part due to the falling prices of imported information technology goods. Expanding the model to capture this is left to future research. Domestic bonds are in zero net supply.

Footnotes

Note that the lag of consumption in the utility function, which appears due to external habit persistence, is based on aggregate consumption, not that of the individual consumer. [3]

In all, there are 12 shocks in the model. [4]

Policy is implemented by the central bank making lump-sum transfers to consumers so as to achieve this interest rate. Our measure of value added is defined as 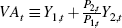. [5]