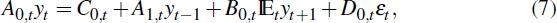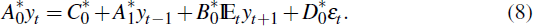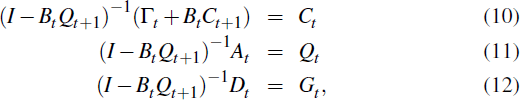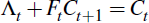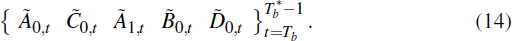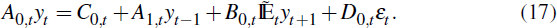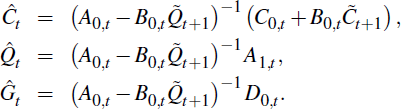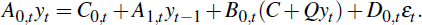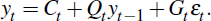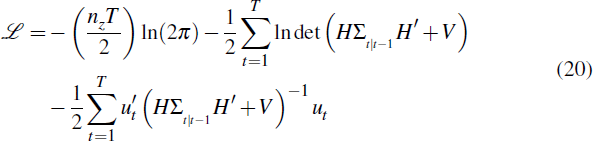RDP 2012-08: Estimation and Solution of Models with Expectations and Structural Changes 3. Solutions with Structural Changes

Before we discuss solutions to the different cases, it is useful to introduce some notation. First, there is a sample of data running from t = 1,2,…,T. Second, we allow for a number of structural changes over the sample period. Hence we begin by assuming that the first structural change is at T_m and the last is at 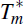. Accordingly, the initial model is replaced by a new one at T_m, following which there may be a sequence of models until 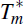, when a final model is in place. After 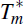no further structural changes are assumed to take place (and we will say that the structure has converged). Notice that, given these definitions, if there is just a single structural change then it begins at 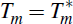, since the model after the initial one is the final model.

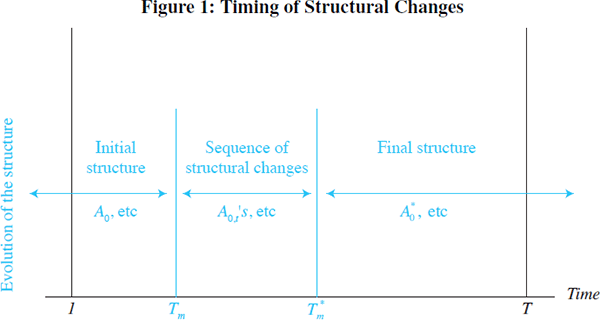
Figure 1 illustrates one possibility. The arrows describe the evolution of the structure. The sequence of structural changes begins in T_m and ends in 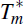. In Figure 1, just as in our later examples, T_m and 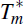take place in-sample, although nothing about our solutions requires this to be the case. Further, in practice, one might also have many structural changes in the model parameters (and these could possibly overlap); it suffices to establish the solutions with a single sequence of structural changes.

A formal account of the description above follows. Formally it is being assumed that before T_m the structure is stable at Equation (1). Then, during t = T_m,…, 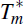– 1 the structure evolves as

subsequently changing over during t = 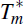, …, T to

Thereafter, there are no further structural changes and Equation (8) holds into the infinite future.

To be concrete suppose there are two structural changes in the sample. In the first interval (1 to T_m – 1) there is a model whose coefficients are θ = {A₀,C₀,A₁,B₀, D₀}. In the second interval (T_m to 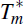– 1) these change to 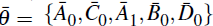. and in the final interval 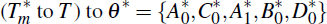. The notation in Equation (7) allows the parameters A_0,t etc to vary according to the time period but in the two structural change case A_0,t = 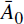etc from T_m to 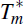– 1 and after that the structure converges to 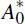etc. In general, when a sequence of structural changes takes place in-sample, the structural matrices are given by .

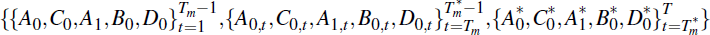In the first numerical example of Section 4 we will consider a single structural change as opposed to a sequence of them, and so we will often refer to the interval t = 1,…, 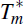– 1 as the ‘first interval’ and t = 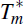,… as the ‘second interval’. The second of our illustrations in Section 4 refers to two structural changes.

3.1 Regime Shifts with Beliefs Matching Reality

As seen in the solution method for models without structural change, a key element is to replace the forward expectations with a function that is consistent with the existing model and the information agents possess. Thus we need to specify how expectations are to be formed at a point in time and what information is available to agents at that point. We consider two cases. In the first case we take agents' beliefs about the prevailing structure to be accurate (i.e. beliefs match reality). The sequence of structural changes given by Equations (7) and (8) are taken to be known once they occur. In the second case it is assumed that the sequence of structural changes given by Equations (7) and (8) is foreseen from T_m. In particular, from period T_m onwards agents know when all future structural changes occur i.e. at the time of the first structural change they know exactly when future changes will take place.^[3]

3.1.1 Structural changes known once they occur

To begin, take the simple case of a single structural change. Up until 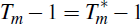, agents will assume that the first interval model with coefficients θ = {A₀,B₀ …} is going to continue indefinitely. Hence the solution is that for the no structural change case i.e. y_t = C + Qy_{t – 1} + Dε_t. From 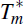onwards, agents form expectations with the final model that has coefficients 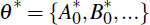and so the solution will be y_t = C^* + Q^* y_{t – 1} + D^* ε_t. So one simply uses the model that holds at any point t to compute the solution for y_t. Clearly, the solution generalises to any number of structural changes.

3.1.2 Foreseen structural changes

Now consider what happens if, after the first structural change, agents know when all future changes will take place. In this situation expectations need to be formed which recognise that agents know that different model(s) will hold at some point in the future. In general, from T_m onwards the solution for y_t at any point in time will be a time-varying VAR of the form

Because the information about future structures (models) is taken to be certain and non-stochastic, it follows that 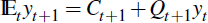. Then, following the earlier solution method, we would get the equivalent conditions to Equations (4) to (6) as

where, as before, 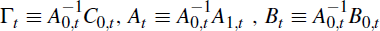and 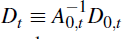. There are two key differences. One is the second condition which now becomes

so that to solve for Q_t we need to use a backward recursion. To do so, we start from the solution of the final structure 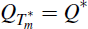, and choose the sequence 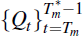that satisfies Equation (13). The second difference is the first condition which can now be written as

where Λ_t = (I – B_tQ_t+1)⁻¹ Γ_t and F_t = (I – B_tQ_t+1)⁻¹ B_t With Q_t in hand it is possible to solve for C_t through a forward recursion, giving C_t = Λ_t + F_tΛ_t+1 + F_tF_t+1Λ_t+2+…

To illustrate, consider the case of two structural changes. From T_m onwards agents know about any future structural changes. Starting with the final interval 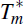,…,T, since the final model is in place from 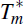onwards one can apply the no structural change solution method to get a VAR structure y_t = C^* + Q^*y_t−1 + G^*ε_t.

Accordingly, this applies to the last interval and enables us to determine that 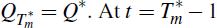the second interval model with coefficients 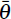is in place but agents know that the final model holds at 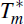onwards, so they account for this when forming expectations. Hence one solves for 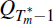using the backward recursion in Equation (13) but with 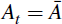etc. Before T_m the data are generated by the initial model with coefficients θ, that is by the first interval VAR structure y_t = C + Qy_t−1 + Gε_t.

Hence in the interval, 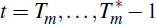, the solution is a time-varying coefficient VAR with the movements in its coefficients being pinned down by the way the structure changes and is expected to change. Notice that the backward recursion implied by Equation (13) makes Q_t a function of Q_t+1. This means that the weights used to form expectations at time t are a function of current and future structures (models).

3.1.3 Announcement effects

Announcement effects, such as happens with the introduction of a goods and services tax (GST), the formation of a common currency, etc, can be captured in the set-up above. If there is a single regime shift which is known in advance of when it occurs then the initial model would hold for 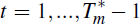and the final model from 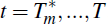. The date of the break, 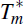, is the time when the final model is in place. However, agents may now learn about the forthcoming change at, say, T_a. We would choose the sequence 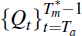starting from 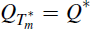as before, such that A – Qt + BQ_t+1Q_t = 0. Although for 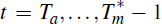, the structure remains constant (i.e A_0,t = A₀, C_0,t = C₀, etc), the announcement itself triggers a drift in the reduced form. In fact, between the announcement date, T_a, and the implementation date, 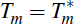, the reduced form drifts from the first interval VAR structure y_t = C + Qy_t−1 + Gε_t towards the final interval VAR structure, yt = C^* + Q^*y_t−1 + G^*ε_t.

3.2 Regime Shifts Where Beliefs are Different from Reality

In the analysis above, beliefs agree with reality. When the structural changes are unknown until they occur, expectations are formed at each point in time using the model that pertains to that period of time. When agents foresee the structural changes, and the structural changes do take place, they know both the new and old models and therefore form expectations by weighting the information appropriately at each point in time. In this section we deal with the more general case in which this may not always be true. In doing so we assume agents do eventually use the correct model but there may be a period of time in which they are mistaken about which structure (model) holds. Hence, during that interval, they may form incorrect expectations: expectations are model consistent, but consistency may be with the wrong model for part of the sample period.

We introduce notation for the timing of beliefs. We denote by T_b the time when agents update their beliefs about current and future structures and by 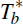the time when beliefs agree with the final structure. We impose no restrictions between T_m and 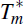on one hand andT_b and 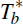on the other, so that beliefs may converge before or after the structure has converged and they may be updated before or after the first structural change.

One possibility is illustrated in Figure 2. The lower arrows describe, as before, the evolution of the structure while the upper arrows now describe the evolution of beliefs. The sequence of structural changes begins in T_m and ends in 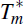, with beliefs being based on the wrong structure (model) for some time. Beliefs are first updated in period T_b, after the structural changes begin, and converge in period 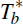, after the structure has converged.

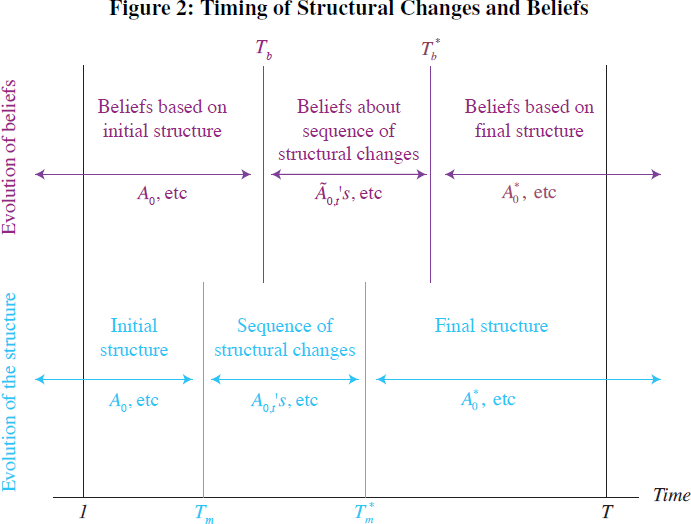
This generalisation allows us to consider situations in which agents do not get the timing of the structural changes right, as well as capturing situations of imperfect credibility in which policy announcements may be carried out as announced, but are not necessarily fully incorporated into expectations formation.

We assume the structure evolves as before: that is, before T_m the structure is stable at Equation (1). Then, during , the structure evolves as in Equation (7), subsequently changing for to Equation (8). Agents' beliefs, however, may evolve differently. Before T_b, expectations are based on Equation (1) while after T_b agents believe that the structural coefficients will evolve as follows:

Subsequently beliefs change for to Equation (8), the final structure. Equation (14) indicates that, in the period up to 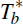, agents may have inaccurate beliefs about which model is generating the data. In the special case that A_0,t = Ã_0,t etc, T_m = T_b and 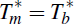beliefs are always accurate and the situation coincides with the one discussed in Section 3.1.2.

In terms of our single structural change example, the period up to 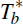may have a period of time over which the initial model holds and a further period in which the final model holds. From max 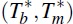onwards it is only the final model that generates the data.

Given this departure from the standard rational expectations context, we assume agents combine observed outcomes with their beliefs about the structure to compute the time t conditional expectation, 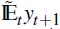, where the notation emphasises that expectations are based on Equation (14).^[4] In this case, agents use their model beliefs to determine weights to be applied to observed data when forming expectations. When agents believe the structure will evolve as in Equation (14), one proceeds as before, starting from 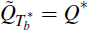to find the sequence 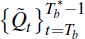such that

The solution agents would infer for 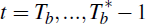is

which implies that 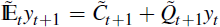However, the actual path of the economy obeys

Using Equation (16) it is easy to show that the reduced-form VAR is given by

where

The solution in this case also takes the form of a time-varying coefficient VAR with movements in its coefficients being pinned down by the way the structure evolves as well as agents' beliefs about these structural changes.

When the structural changes begin before agents first update their beliefs (i.e. T_m < T_b) as is the case in Figure 2, expectations are based on the initial structure in those periods, that is 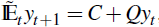, so the economy in those periods follows

With 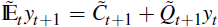in hand, other cases, 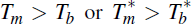, are straightforward to compute.

3.3 The Likelihood

As we have discussed above, a set of structural changes and assumptions about beliefs and expectations formation map into a sequence of reduced-form matrices. If the structural changes are unknown until they occur, the solution is computed as in Section 3.1.1. If the structural changes are foreseen, the system follows Equation (9), and in the more general formulation where beliefs may differ from reality, the system follows Equation (18). The derivation of the likelihood is identical in each case since each involves a reduced form. Therefore, with no loss of generality, let the reduced form be given by Equation (9):

Now assume that we have in hand a sample of data, 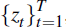, where z_t is a n_z × 1 vector of observable variables that relate to the model's variables by

In Equation (19), v_t is an iid measurement error with 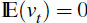and 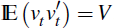. The observation equation, Equation (19), and the state equation, Equation (9), constitute a state space model. Therefore, the Kalman filter can be used to construct the likelihood function for the sample 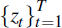as outlined, for example, in Harvey (1989). Appendix A provides details of the derivation of the log-likelihood in Equation (20).

In Equation (20), 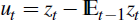is the prediction error,

View MathML

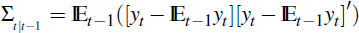
is the covariance matrix of the state variables y_t conditional on information at t – 1, and cov_t−1(z_t) = HΣ_t|t−1 H′ + V.

With Equation (20) in hand, standard likelihood-based tests for parameter stability and detection of date breaks are available.^[5]

Footnotes

It will be obvious from the solution method that we can handle situations where only some of the future structural changes are known at T_m. [3]

One could alternatively assume that agents utilise their beliefs about the model to produce both the weights and values for the endogenous variables themselves when computing expectations, i.e. they project a model consistent path for the endogenous variables which will be incorrect if model beliefs are incorrect. There are other reasonable assumptions as well. For example, we could assume that either only lagged outcomes are observed or that only some subset of the variables are observed at time t. These extensions are left for further research. [4]

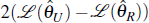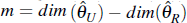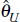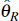Under the null hypothesis of no structural change the likelihood ratio statistic, , is asymptotically distributed as a chi-square random variable with degrees of freedom, where is the unrestricted maximum likelihood estimate of the vector of structural parameters and is the restricted maximum likelihood estimate of the vector of structural parameters after imposing the restrictions of no structural change. Detection of structural change is generally done with a recursive likelihood ratio test. [5]