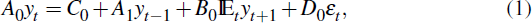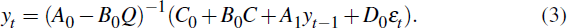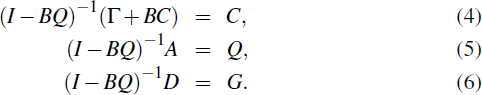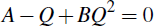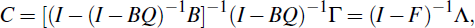RDP 2012-08: Estimation and Solution of Models with Expectations and Structural Changes 2. Solution of Models with Forward-looking Expectations and No Structural Changes

Our solution method is a variant of Binder and Pesaran (1997). Following that paper, a linear rational expectations model of n equations can be written as

where y_t is a n × 1 vector of state and jump variables and ε_t is a l × 1 vector of exogenous variables. With no loss of generality we take the latter to be white noise and to have I_l as their covariance matrix. All matrices in Equation (1) conform to the specified dimensions.^[2] The formulation can be generalised as in Binder and Pesaran (1997) to allow additional lags of y_t as well as conditional expectations at different horizons and from earlier dates.

If it exists and is unique, the solution to Equation (1) will be a VAR of the form

Given that this is the solution and 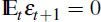we must have 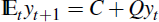. Substituting this into Equation (1) and re-arranging terms produces

Now 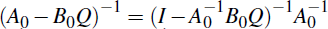and defining 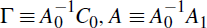, , 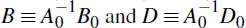Equation (3) becomes

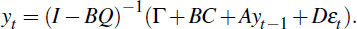
But this must equal Equation (2), establishing the equivalences

Equation (5) implies that

and so determines Q. Equation (4) implies that

where Λ = (I – BQ)^-1Γ, F = (I – BQ)^-1B. Thus, once Q is found, it is possible to derive C and G, providing the solution to the model.

Footnote

We may need to make a distinction between the original shocks of a dynamic stochastic model, e_t, and the shocks ε_t in Equation (1). Often e_t are taken to be serially correlated. This can be captured by writting such a system in the form of Equation (1) with lagged values of the endogenous variables included in y_t. This means that ε_t are the innovations to the shock processes e_t. There may be a numerical advantage to working with e_t rather than ε_t, as that reduces the dimension of y_t and, consequently, all the matrices involved in finding a solution. But there are conceptual advantages in using the system we work with. Our MATLAB function that computes the Binder Pesaran solution, ‘smatsbp.m’, does allow us to work with an e_t that is described by a VAR process. [2]