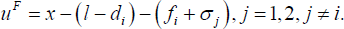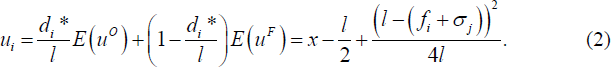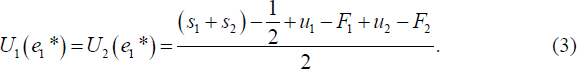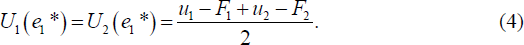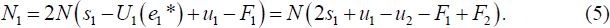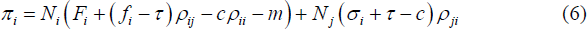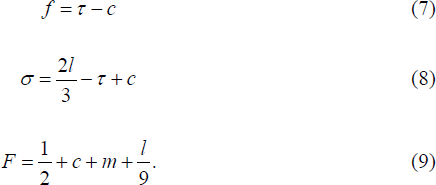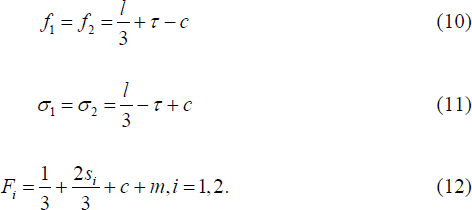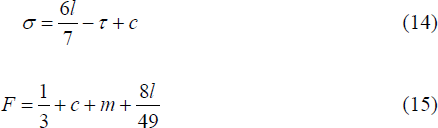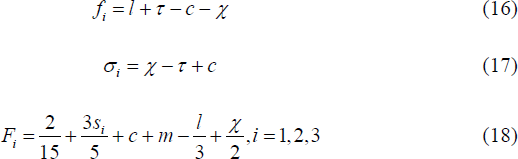RDP 2012-03: ATM Fees, Pricing and Consumer Behaviour: An Analysis of ATM Network Reform in Australia 4. The Model and Implications

This paper develops a model that captures the salient features of the Australian ATM market as described in Section 2. The aim is to model the short-run effect that eliminating interchange fees has on foreign, direct and account-keeping fees, and ultimately on the price consumers pay for foreign ATM transactions. The potential effects on optimal ATM deployment decisions, and other long-run decisions, are ignored in order to focus on short-run pricing dynamics.

The model is based on Croft and Spencer's (2004) model of ATM networks. As the model is intended to focus on ATM pricing behaviour, bank branches are removed from the Croft and Spencer model, as are fees charged on own-bank ATM transactions since they are generally not levied in Australia.^[12]

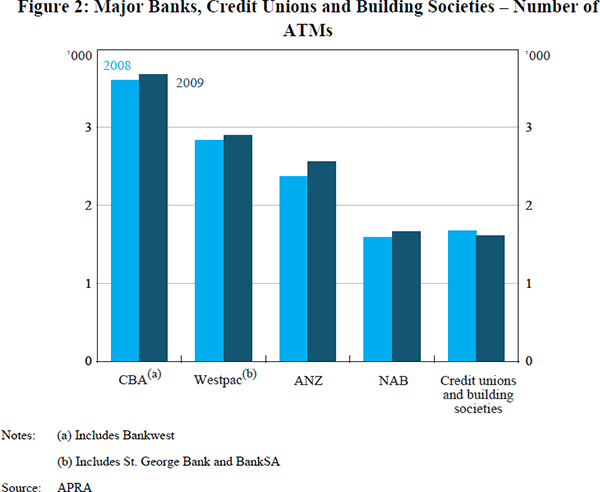
The assumption that each bank has the same number of ATMs is retained, as this is a close approximation to reality in Australia prior to the reform (see Figure 2),^[13] though as in Croft and Spencer (2004) we abstract from the presence of non-bank (that is, independent) ATM operators. Given the evidence of switching costs in the market for deposit accounts (Zephirin 1994; Sharpe 1997), the model explores two different scenarios based on the extent to which deposit account customers are locked in to their existing bank – full lock-in and no lock-in – noting that the degree of depositor lock-in in the Australian market lies somewhere between these two extremes. A two-bank version of the model is solved first, before considering a three-bank version.

In addition to developing a model that captures the key features of the Australian reform, this paper makes a number of novel contributions to the literature. First, explicit solutions are obtained for banks' profit-maximising level of fees. Second, the own-bank processing cost is taken into account and the relationship between this cost and ATM fees is shown; this is useful in understanding why virtually all foreign fees were ultimately eliminated after the reform even though Australian banks had earlier cited own-processing costs as a reason for keeping foreign fees above zero. Finally, the three-bank model is believed to be the first to consider the determination of ATM fees where there are more than two banks. This final contribution is important as banking markets are more likely to be characterised as oligopolistic, or even competitive, rather than duopolistic.^[14]

4.1 Model Set-up (Two Banks)

Our model initially consists of two banks, B¹ and B², which each deploy M ATMs symmetrically spaced and interleaved around a circular city. The city has circumference l^* so the distance between ATMs is l = l^*/2M (Figure 3). There are N consumers distributed uniformly around the city who each have a deposit account at one bank and make one ATM transaction.

Two versions of this model are considered – one where customers are locked-in, and one where they are not. In the locked-in model timing is as follows: (i) the interchange fee is set (this fee is taken as given by both banks and customers); (ii) banks set their account-keeping fee; (iii) customers choose a bank to open a deposit account with; (iv) banks set their other ATM-related fees; (v) consumers are randomly located around the circular city and make ATM withdrawals. In the model without lock-in: (i) the interchange fee is set; (ii) all bank fees are set; (iii) consumers choose a bank to open a deposit account with; (iv) consumers are randomly located around the city and make their withdrawals. The consumers' problem of choosing which ATM to use, given all fees, is common to our two models. This is solved first. Then the consumers' bank-choice problem and the banks' profit maximisation problem to determine fees are solved.

Bank i, for i = 1, 2, charges consumers three types of fees: an account-keeping fee F_i to each deposit account customer (hereafter, customer); a foreign fee f_i for any transaction carried out by a customer of bank i at a foreign ATM; and a direct fee σ_i for any transaction carried out by a non-customer using one of bank i's ATMs. A customer receives utility x for making an ATM withdrawal as well as disutility equal to the distance travelled to the ATM plus any fee incurred.^[15] A list of definitions is found in Appendix B.

4.2 The Consumer's ATM Problem (Two Banks)

Consider a customer of bank i and let the distance to an own-bank ATM be d_i. The utility from making an own-bank withdrawal is u^o = x − d_i. The utility from making a foreign withdrawal is:

Where the distance to the foreign ATM is l − d_i and the cost consists of the own-bank foreign fee f_i plus the foreign bank's direct fee σ_j. The customer is indifferent between the own and foreign ATM if u^F = u^o, which occurs at:

That is, bank i customers will use own-bank ATMs up to a distance of d_i^* away, after which they will use a foreign ATM. An immediate implication is that f_i + σ_j < l is needed if customers are not going to always use own-bank ATMs.

Prior to the final stage, consumers do not know where in the circular city they will be located, but do know that they will be randomly and uniformly distributed around the city. Consequently, prior to the final stage, consumers make decisions based on the expected utility from making ATM withdrawals.

Since consumers are distributed uniformly around the circular city in the final stage, on average a proportion d_i^*/l of bank i customers will travel a distance d_i ≤ d_i^* to use an own-bank ATM; the remaining proportion of bank i customers (1 − d_i^*/l) will travel a distance (l − d_i^*) ≥ d_i to use a bank j ATM. Correspondingly, a customer of bank i that uses a bank i ATM (to undertake an own-bank ATM transaction) will, on average, travel d_i^*/2 and achieve expec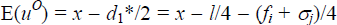ted utility from that transaction. A customer of bank i that uses a bank j ATM (to make a ‘foreign’ ATM withdrawal) will, on average, travel (l − d_i^*)/2 and receive expected utility 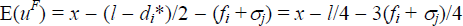from that transaction.

Without knowing his final stage location, a customer of bank i anticipates total expected utility from ATM services, u_i, of:^[16]

4.3 The Consumer's Bank-choice Problem (Two Banks)

Along with ATM services, it is assumed that banks provide other general services that consumers value such as internet banking, automated transfers and teller service. In this model, consumers' tastes with regard to these services are uniformly distributed on a unit circle and bank 1 and 2's offerings (denoted s₁ and s₂) are situated at opposite sides of this circle. It is assumed that a consumer with distance in taste e_i from bank i gains gross utility (that is, before fees are paid) of s_i − e_i from an account with bank i, and gross utility of s_j − (1/2 − e_i) from an account with bank j, where 1/2 − e_i is the distance to s_j.

Given the above, a consumer with taste parameter e₁ gains total expected utility (that is, the utility from general banking services and ATM use net of fees) of U₁(e₁) = s₁ − e₁ + u₁ − F₁ from an account with bank 1 and U₂(e₁) = s₂ − (1/2 − e₁) + u₂ − F₂ from an account with bank 2.[ ¹⁷] For a given level of fees, the marginal consumer has taste e₁^* satisfying:

As consumers' tastes are uniformly distributed around a unit circle, the total expected utility of the marginal consumer depends on the total quantity of general banking services offered, s₁ + s₂, rather than the relative amount of general services provided by each bank. Given this, for computational simplicity, and following Croft and Spencer (2004), the total quantity of general services offered is normalised such that s_i + s_j = 1/2. This simplifies the marginal consumer's total expected utility to:

This quantity must be positive to ensure that all consumers open accounts.^[18]

Finally, since tastes are uniformly distributed, there are N₁ = 2e₁^*N consumers with e₁ ≤ e₁^* who choose bank 1, and N₂ = N − N₁ consumers with e₁ > e₁^* who choose bank 2. Since 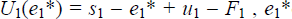can be found and it can be shown that:

This is an intuitive result. It implies that the number of deposit account customers bank i attracts, N_i, is decreasing in the account-keeping fee it charges and increasing in the quantity of general services it provides. The number of bank i customers is also increasing in both the account-keeping fee charged by its rival (bank j) and the difference in utility that its customers would derive from using an own ATM over a ‘foreign’ ATM.

4.4 The Bank's Problem (Two Banks)

Banks derive revenue from fees charged to customers and (in the pre-reform regime) the interchange fee charged to the other bank. For each foreign customer who uses one of bank i's ATMs, bank i receives the interchange fee, denoted τ, from the foreign customer's bank. In our model this fee is exogenous and reflects either an amount previously agreed upon between banks (the Australian case pre-reform), or an amount set by the regulator (the Australian case post-reform). Banks also face three costs: the interchange fee, τ, that must be paid each time one of their deposit account customers uses a foreign ATM; the common ATM usage cost c incurred when an ATM they own is used, either by their own deposit account customer or a foreign customer; and an own-bank processing cost m incurred when a deposit customer of theirs withdraws cash from either an own-bank or foreign ATM.^[19]

Given these fees and costs, bank i's profit is given by:

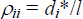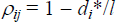where is the proportion of bank i customers who use a bank i ATM, and is the proportion of bank i customers who use a bank j ATM. That is, bank i profits from its N_i customers from an account-keeping fee F_i, as well as its foreign fee (less the interchange fee) in proportion to own customers using foreign ATMs, (f_i − τ)ρ_ij. Own customers cost the bank the ATM usage cost in proportion to their use of own-bank ATMs, cρ_ii, as well as the own-bank processing cost, m. Bank i also profits from the N_j bank j customers by its direct fee plus the interchange fee it earns, less the ATM usage cost, all in proportion to bank j's customer's use of foreign (bank i) ATMs, (σ_i + τ − c)ρ_ji.

4.5 Solving the Non Locked-in Model (Two Banks)

To solve the banks' problem and determine the Nash equilibrium for F_i, f_i and σ_i, π_i is maximised, for i = 1, 2, subject to the constraints that u_i − F_i ≥ 0 and u_j − F_j ≥ 0 which, from Equation (4), ensures that all consumers open bank accounts. In the symmetric case s₁ = s₂ = 1/4, where each bank provides the same level of general banking services^[20] and charges the same fees, all bank fees can be explicitly calculated as functions of the model's parameters. These explicit forms for bank fees are a new result of this paper, and are given below (see Appendix C for derivations):

Because customers choose banks after all fees have been set in this case, banks have an incentive to set ATM fees to attract customers and earn the account-keeping fee. Each bank does this by charging (or subsidising) own customers for foreign ATM use so as to just cover the marginal cost of the transaction, τ − c, as shown in Equation (7).^[21] Conversely, Equation (8) shows that foreign customers are charged 2l/3 more than marginal cost to use an ATM.^[22] These fee strategies (of only charging deposit customers the marginal cost for making foreign withdrawals, while charging foreign customers a direct fee that is greater than the marginal cost) increase the attractiveness of being a customer of the bank.

Equations (7) and (8) imply that when interchange fees are not permitted (that is, when the regulator sets τ = 0), the foreign fee will fall by the amount of the interchange fee while the direct fee will rise by this amount, leaving the total price of foreign ATM withdrawals unchanged at 2l /3.

Equation (9) gives the account-keeping fee, F, which allows the cost of ATM use, c, the own-bank processing cost, m, as well as part of the consumer surplus to be recovered.^[23] Equations (6) and (8) show that, at least in this model, contrary to the claim of some Australian banks, profit-maximising banks will recover the own-bank processing costs of ATM transactions through account-keeping fees rather than the foreign fee, since this cost is incurred irrespective of whether customers use own or foreign ATMs.^[24] It therefore follows that the presence of own-bank processing costs need not necessarily imply foreign fees that are strictly positive.

In the more general case, where s₁ ≠ s₂ ≠ 1/4 so that the level of banks' general services differ, an explicit form solution can only be obtained for the foreign fee.

In this case, the foreign fee is identical to the symmetric case and is given by f_i = τ − c for i = 1, 2.^[25]

4.6 Solving the Locked-in Model (Two Banks)

The locked-in model can also be solved and an explicit solution is derived in Appendix C for the general model where banks need not provide a symmetric level of general services. This explicit solution, a novel result of this paper, is given by:

Equations (10), (11) and (12) are similar to Equations (7), (8) and (9), although there are a few differences. As deposit customers are locked-in at the point of ATM fee determination, banks no longer have an incentive to set ATM fees strategically to attract (or retain) deposit customers. Hence, they increase their foreign fee relative to the non locked-in case, raising the per transaction ATM revenues from their deposit customers. In the non locked-in case, increasing foreign fees drives deposit customers away and so gains in per customer ATM revenue come at the cost of losing revenue from the account-keeping fee. At the same time, the direct fee, which penalises customers of the other bank, is reduced. Overall though, the total price of a foreign transaction is the same as in the non locked-in case and interchange fee neutrality continues to hold, as does the implication that foreign and direct fees will shift by an amount equal to the interchange fee when the interchange fee is banned.

It is also interesting to note that both banks choose the same level of fees, even in the non-symmetric case. This is because, while banks are asymmetric in the level of general services they offer (and as a result attract different numbers of customers), once customers are locked-in, the two banks' profit maximisation problems are essentially the same, except for a scale factor (compare Equations (C8) and (C9)).

In the symmetric case, the account-keeping fee is also lower in the locked-in model. This reflects the fact that in the locked-in case, banks compete more aggressively in setting account-keeping fees, knowing that the deposit customers they secure cannot subsequently switch banks in response to foreign or direct fees.^[26]

4.7 The Three-bank Case

The intuition behind the three-bank case is similar to the two-bank case and so the model development is left to Appendix C. The main difference is the existence of a discontinuity in the profit function when there are three banks.^[27]

In this model, the cost to the consumer of walking from a foreign ATM to an own-bank ATM is l (Figure 4).^[28] As a result, if the total cost to the consumer of using a foreign ATM is less than or equal to l then at least 1/3 of customers will use foreign ATMs; this is because 1/3 of consumers will be located between two foreign ATMs and, with the total cost less than or equal to l, they will not find it worthwhile to walk past either foreign ATM to use an own-bank ATM. Conversely, when the total cost is greater than l, no consumers will use foreign ATMs as even those located between two foreign ATMs will find it worthwhile to walk past the foreign ATMs to use an own-bank ATM.

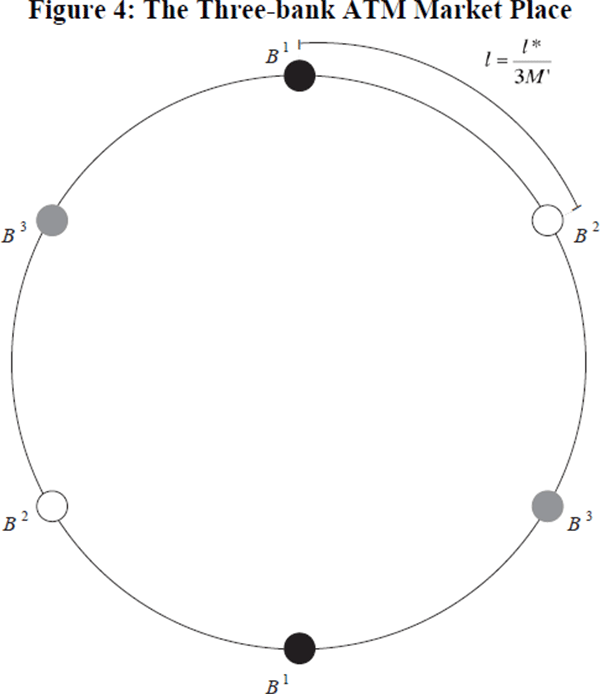
In the symmetric non locked-in case, the discontinuity noted above does not affect the solution, which is given by:^[29]

As with the two-bank case, banks strategically set foreign fees and direct fees to attract customers. As the density of ATMs has been kept unchanged from the two-bank set-up (so that the distance between ATMs is still l, and each bank owns M′ ATMs), own-bank ATMs are now further apart, so banks are also able to raise their overall level of ATM fees relative to the two-bank model.

In the locked-in case, the profit function discontinuity is important. In this case there is a continuum of Nash equilibria characterised by the parameter χ, which lies between 0 and l/2 (see Appendix C for proof):

Each of these equilibria results in the consumer paying the same total price, f_i + σ_j = l, for a foreign ATM transaction, and implies interchange fee neutrality.^[30] Importantly though, the presence of a spectrum of equilibria means that foreign and direct fees need not adjust in lock-step with the interchange fee. Rather, the possibility of an exogenous shift to another equilibrium point on the continuum (that is, a change in χ), allows foreign and direct fees to move independently of the interchange fee.

The range of values χ can take describes the suite of stable equilibria that can exist in the market. The actual value χ takes can be thought of as capturing the historic context of the market. A change in χ reflects a shift in the status quo. In the Australian case, it is plausible that public pressure from the Reserve Bank for foreign fees to be set at or near zero post-reform triggered such a shift (see Section 2.1).

This model, therefore, provides a mechanism to explain the post-reform changes observed in ATM fees in Australia. In this case, interchange fees of around $1.00 were eliminated, but foreign fees fell from $2.00 to zero and direct fees rose from zero to around $2.00. That is, foreign and direct fees adjusted by twice as much as the change in the interchange fee. In this model, such a change could be explained by a move to a new point along the spectrum of equilibria (via an increase in χ). Specifically, the change in fees observed in Australia is generated by the three-bank model when an interchange fee of τ = 1 is prohibited, χ shifts from 0 to 1, and the cost of providing ATM services and distance between ATMs are given by c = 1 and l = 2.

Footnotes

Croft and Spencer assume that own-bank ATM fees are set at marginal cost. This is limiting in the Australian case as banks do not typically charge for own-ATM withdrawals. Using this assumption, the model cannot capture the incentive banks may have to discourage own-ATM use (because the fee charged – zero – is below marginal cost) and/or subsidise foreign ATM use, which happens in some cases, for example Bankwest (2010) and ING Direct (2010). [12]

The shared ATM network of the credit unions and building societies was also of a comparable size to the networks of the large Australian banks. [13]

Donze and Dubec (2006, 2008) do consider an ATM market with more than two banks, but only in the scenario where banks do not charge consumers fees for ATM transactions (that is, foreign fees, direct fees and own-bank ATM usage fees are not considered). [14]

Travel costs are captured by the parameter l (which depends on l^* and M). For a given number of ATMs, the average travel cost to withdraw cash increases with the circumference of the circular city. [15]

For any given x there exists an l small enough (or M large enough) to ensure that expected utility is positive. If the number of ATMs is too small the network will not be viable. [16]

Recall that u₁ and u₂ are functions of f_i and σ_i, i = 1, 2. In the non locked-in case the consumer will know the (fixed) values of f_i and σ_i explicitly and hence know u₁ and u₂; in the locked-in case the consumer will know, given a set of other model variables, how the banks will choose f_i and σ_i, although they may not know the explicit values chosen. [17]

This constraint can be thought of as a universal service obligation imposed by the regulator. [18]

The ATM usage cost c reflects ATM maintenance costs such as cash refilling for example. [19]

But not necessarily the same type of banking services. [20]

The customer's bank must pay the interchange fee τ when a customer uses a foreign ATM. Conversely, a customer who makes a foreign ATM withdrawal does not make an own-bank withdrawal, saving the customer's bank the ATM usage cost c. [21]

Heuristically, in Equation (8) the term 2l is divided by three due to the common direct fee, σ, appearing three times in the lagrangian that describes bank i's constrained optimisation problem; once in the profit function (as the bank derives revenue from charging a direct fee) and once in each of the two constraints that ensure consumers open bank accounts (as these constraints essentially state that the ATM fees, σ and f, must not be so large that accounts are not opened). For the same reason, in Equation (9) the term l is divided by 9 = 3². For the precise derivation, see Appendix C. [22]

Note that banks subsidise deposit customers' use of foreign ATMs by c. [23]

More specifically, as each bank incurs the own-bank processing cost, m, each time their deposit customers use either a foreign ATM or an own-bank ATM, and as the number of transactions each customer makes is known to the banks when the account-keeping fee is set, this cost is most profitably recovered through the account-keeping fee. Heuristically, if m was recovered in the foreign fee, and not in any other fee, the banks would only recoup the own-bank processing costs incurred from their customers' use of foreign ATMs but not the own-bank processing costs incurred by their customers' use of own ATMs. [24]

Although the result cannot be proved explicitly, solving the non-symmetric model numerically for a range of model parameters also resulted in neutrality of the interchange fee. [25]

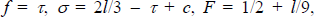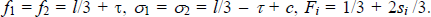We can also solve a version of the Croft and Spencer (2004) model with no bank branches and compare results to those of our model. In the symmetric non locked-in case we find that while in the general locked-in case we find that By assumption, banks charge their customers the marginal cost c for own-bank ATM transactions in the Croft and Spencer model, so there is no incentive to subsidise customers to make foreign transactions and the total price of a foreign ATM transaction is higher by c than in our model. The account-keeping fee in the Croft and Spencer model is also lower by c + m since the foreign fee is now not subsidised by c and the processing fee m is not considered. We omit proofs as they are similar to those of our model given in Appendix C. [26]

The discontinuity arises because some customers are located between two foreign ATMs in the final stage. This occurs when banks' ATMs are distributed symmetrically and there are three or more banks. The discontinuity could also arise with just two banks if the banks' ATMs are not symmetrically distributed and interleaved; specifically, a bank would need to locate two or more of its ATMs adjacent to each other. [27]

A customer that is indifferent between own and foreign ATM use is assumed to use the foreign ATM. This assumption is only for notational convenience and does not change the results. [28]

Heuristically, in Equation (14) the term 6l is divided by 7 due to the common direct fee, σ, appearing seven times in bank i's total profit function; twice directly, as direct fee revenue is gained when the deposit account customers of the other two banks use bank i's ATMs, and five times indirectly through the ρ terms that describe the proportion of a given bank's customers that use a particular ATM network. For the same reason, in Equation (15) the term l is divided by 49 = 7². For the precise derivation, see Appendix C. [29]

In fact, a total price l for foreign ATM transactions corresponds to the joint profit-maximising level of ATM fees. [30]