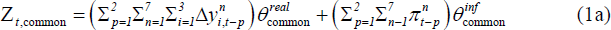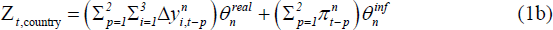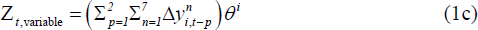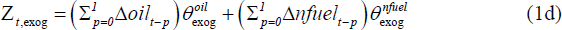RDP 2012-01: Co-movement in Inflation 3. A Panel VAR
March 2012 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 814KB
The panel VAR model outlined below largely follows Canova et al (2007) and Canova and Ciccarelli (2009).[4] In this section we outline the key features of the approach. A detailed description of the model and the estimation procedure can be found in Appendix A.
A panel VAR represents an extension of a standard dynamic panel data model to incorporate a vector of variables. In this paper, the G7 economies make up the cross-sectional dimension of the panel, while the ‘VAR’ part consists of four endogenous variables (output, consumption, investment and the CPI). We also include oil and non-fuel commodities prices (in SDR terms).[5] Initially we treat the commodity variables as exogenously determined but later relax this assumption. The data are quarterly and all variables enter the model in log-differences.
We choose to focus on the G7 economies for two reasons. First, the G7 represents a reasonably homogenous group of economies, in that they are advanced economies with well-developed financial sectors and institutions, and broadly similar policy frameworks. As we will see, the panel VAR approach we employ imposes certain similarities on the equations governing the endogenous variables in the model. It is more appropriate then in our application to consider a group of countries that are somewhat similar. Second, this group of countries is well studied and allows our results to be compared to others in the literature. This is not to suggest, however, that other regions, for example, Latin America or east Asia, are unimportant for the study of global inflation, but rather that it is difficult to include a truly global sample of countries using our framework. We also exclude Australia from entering the panel VAR as it is small in a global sense and later we will investigate the significance of co-movement in inflation for modelling inflation in Australia in a separate model.
3.1 The Model
The panel VAR can effectively be thought of as a relatively large VAR, with variables for a number of different countries endogenously determined. For each country, domestic variables are modelled not only as a function of own past lags and other domestic variables, but also as a function of the variables of all other countries. These cross-country lagged interdependencies increase the flexibility and realism of the model and its ability to capture interesting dynamics, such as spillover effects across countries and variables.
It is not feasible, however, to estimate the large number of parameters in a VAR containing 28 endogenous variables (7 countries and 4 variables per country) using the length of data available.[6] Therefore, following Canova et al (2007) and Canova and Ciccarelli (2009), we employ a factorisation of the model's coefficients that effectively re-parameterises the panel VAR such that the endogenous variables we want to explain depend on a smaller number of observable factors or ‘indicators’. These indicators essentially summarise the key drivers of a larger set of variables, in a similar fashion to factor models.[7] Equivalently, the approach can be seen as imposing certain restrictions on the parameters of the large VAR. Prior to estimation the data are de-meaned and standardised (as is common practice when working with factor-type models), implying equal weight is given to each country in the panel VAR.
The indicators are, by construction, linear combinations of certain right-hand-side variables of the panel VAR and highlight co-movement between the different series. The factorisation chosen allows us to investigate the importance of common drivers of the endogenous variables in the panel VAR, relative to country-specific, variable-specific or exogenous influences. To illustrate this more clearly, Table 1 shows how the factorisation would work in a simple two-country, two-variable (and one lag) setting. In this example, there are 5 coefficients to estimate, relative to the 16 there would be in an unrestricted VAR with one lag.
| Equation | Right-hand-side indicators | |||||
|---|---|---|---|---|---|---|
| Country-specific | Variable-specific | Common | ||||
| YA + XA | YB + XB | YA + YB | XA + XB | YA + XA + YB + XB | ||
| YA | βA | 0 | αY | 0 | θ | |
| XA | βA | 0 | 0 | αX | θ | |
| YB | 0 | βB | αY | 0 | θ | |
| XB | 0 | βB | 0 | αX | θ | |
| Notes: Table entries are coefficients to be estimated in the panel VAR | ||||||
Extending this approach to our setting, the equation for variable g in country n is represented by Equation (1).
Equation (1) is representative of all equations in the panel VAR (output growth, consumption growth, investment growth and inflation for each country), with the right-hand-side consisting of:[8]
-
Common indicators – two common indicators are included, one for the real activity variables and one for inflation, giving equal weight to two lags of each variable for all countries:
Where p indexes the two lags, n the seven countries, i the three real variables and
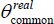 and
and 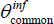 are the estimated
parameters on the real and inflation variables that are common across countries.
are the estimated
parameters on the real and inflation variables that are common across countries.
-
Country-specific indicators – two country-specific indicators, one for the real variables and one for inflation, were constructed giving equal weight to two lags of each variable for a single country:
Where the n subscript on
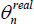 and
and 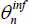 indicates these parameters
are estimated just for country n's block of equations in the
panel VAR.
indicates these parameters
are estimated just for country n's block of equations in the
panel VAR.
-
Variable-specific indicators – constructed giving equal weight to two lags of either output, consumption or investment growth for all countries: [9]
-
Exogenous indicators – constructed giving equal weight to contemporaneous and one lag of both oil price inflation and non-fuel commodity price inflation:
It is important to highlight that when estimating the model we make a distinction between real activity (output, consumption and investment growth) and inflation, with each of the indicators allowed to load with a different coefficient across these two types of equations. The coefficients are, however, restricted to be the same across real variables (except in the case of the variable-specific indicators) and across countries (except in the case of the country-specific indicators). For example, the common real activity indicator is included in each country's output, consumption and investment growth equations and is restricted to have the same coefficient. It is also included in each country's inflation equation but loads with a different coefficient than in the real activity equations. Also, oil prices, for example, are allowed to load differently in real activity and inflation equations.
The key advantage of the factorisation we impose is that there are only 38 coefficients to be estimated, rather than the 1680 coefficients there would be in an unrestricted panel VAR. Also, the indicators constructed above offer a useful economic interpretation, summarising common, country-specific, variable-specific and exogenous information in the panel VAR.
The model was estimated using Bayesian methods over the sample 1981:Q2 to 2011:Q1 (see Appendix A for details). The next section presents the model estimates and uses the indicators described above to investigate the key drivers of co-movement in inflation in the G7.
Footnotes
One key difference is that we do not consider time variation in the parameters. [4]
A full list of data sources is presented in Appendix C. [5]
For each of the NG equations in the panel VAR (N = 7 is the number of countries and G = 4 is the number of endogenous variables per country) there are NGP + CP = 60 coefficients (where P = 2 is the lag length and C = 2 is the number of exogenous variables) for a total number of (NGP + CP)NG = 1680 coefficients in such an unrestricted VAR. [6]
See Canova et al (2007) for a discussion of the key differences between the factors generated here and those derived from other factor modelling techniques (for example, those constructed from principal components analysis). This approach to solving the ‘curse of dimensionality’ problem is similar to that used in the global VAR (GVAR) literature, where a linear combination of foreign variables enter as explanatory variables in the VAR (see Pesaran, Schuermann and Weiner (2004)). The GVAR framework has been used to analyse questions related to international trade, global imbalances and international linkages (Dees et al 2007; Bussière, Chudik and Sestieri 2009) and could also be a useful framework in which to investigate global inflation. [7]
The residual term in Equation (1) is assumed to be normally distributed, although the specific form of the variance depends on the factorisation imposed (see Appendix A for details). For the baseline results we assume an exact factorisation which implies homoskedastic errors. [8]
A variable-specific indicator for inflation was not included as it is identical to the common inflation indicator in our setup. [9]