RDP 2011-03: Urban Structure and Housing Prices: Some Evidence from Australian Cities 2. The Alonso-Muth-Mills Model

We use a version of the well-established model of Alonso (1964), Muth (1969) and Mills (1967), and formalised by Wheaton (1974), with its parameters set to match broad features of a stylised city. Our description of the model and of the results that follow is intentionally non-technical. The intuition is straightforward in most cases, but readers interested in the technical details of the model and its calibration are referred to Appendix A and the articles in the references.

2.1 The Basic Model

The basic Alonso-Muth-Mills model assumes a city with a fixed population and a given income level living around a central business district (CBD).^[1] Each worker travels into the city centre for work. Since commuting is costly and increases with distance from the CBD, households would choose, other things equal, to live closer to the city centre. But not everyone can live close to the city centre, so the price and density of housing adjust to clear the market. In particular, land for housing becomes more expensive closer to the CBD, which prompts home-builders to economise on the use of land by building more dwellings per unit of land, that is by building multi-storey buildings and smaller dwellings, as the cost of an additional square metre rises with building height. Households then choose whether to live in well-located, but smaller and more expensive, housing or in more distant, but larger and less expensive, housing towards the city fringe. The city structure is characterised by higher density and taller buildings close to the CBD and lower density and building heights on the fringe. The overall size of the city will be determined simultaneously by the size of the population, the cost of transport and the value of land in alternative uses, such as agriculture.

The model, like all models, simplifies a more complex reality and has limitations. Some of the simplifications are as follows. First, individuals are assumed to be identical in terms of income and preferences. It is, of course, self-evident that real-world cities are characterised by heterogeneity in incomes and housing, but the basic insights of the model remain even in models that allow for these kinds of heterogeneity (e.g. Anas (1990)). While households' preferences for housing are summarised by their demand for generic ‘housing’, other versions of the model have explicitly included demand for yard space (e.g. Arnott and MacKinnon (1977) and Brueckner (1983)), and the qualitative conclusions of our analysis would be similar with such an extension.

Second, the city is assumed to be monocentric, with individuals travelling only to go to work in a central location. Accordingly, the model does not allow for other business districts within the city (that is, for a polycentric city), or for locations to be considered desirable based on other attributes like proximity to education facilities or leisure activities (such as cultural facilities, beaches, etc). Such attributes, as we show in the case of waterfront suburbs in Section 4, can be important in real-world cities. But the conclusions from the basic model are qualitatively robust to such extensions: see, for example, Henderson and Mitra (1996) for an analysis of a model with multiple employment centres.

Third, the equilibrium is partial, in the sense that it abstracts from developments in other markets, like the labour or capital markets. So, the wage rate and the rental rate on capital are taken as exogenous.

Finally, the model is static and asks what would be the equilibrium structure for a city given certain assumptions. That is, it does not account for the long-lived nature of the housing stock, nor the process of urban change and phenomena such as filtering or gentrification, nor the role of changes in the availability of finance. Instead, the model is best viewed as providing insights into the longer-run determinants of the urban equilibrium.

The model's simplicity helps focus on fundamental forces, likely to matter for all large cities. Indeed, as Brueckner (1987) argues, this simple yet powerful model explains the main observed regularities of the urban structure – including, as will be seen in Section 4, many of the stylised facts of Australian cities.^[2] Furthermore, the model is well suited for the purposes of this paper: namely to understand the impact that different policies and population growth have on the characteristics of the urban equilibrium.

2.2 Parameterisation of the Model

To illustrate the forces that determine the structure of the city in the model, we select parameter values, drawing on the work of Bertaud and Brueckner (2005). In broad terms, we match some characteristics of a large Australian city. In particular, we consider a city with two million residents, who live around a CBD. To match the geography of coastal cities and the need for roads and land for other purposes, we assume that housing construction is only possible in a little less than half of the circle around the centre. The price of land at the city fringe is equal to the cost when used in agriculture, and the price within the city is determined, among other factors, by building costs, transport costs, and household incomes and preferences. Households spend part of their income commuting to the CBD, with the cost rising with distance from the CBD: in calibrating transport costs, we account also for the time spent commuting and value it at 60 per cent of the wage rate. They spend the remainder of their income on housing and other goods, with Cobb-Douglas preferences, allocating around 15 per cent to housing.^[3] Firms use land and capital to build housing around the city, with the production function also Cobb-Douglas. Construction costs rise as additional stories are added, so per square metre costs are lower at the fringe than closer to the CBD.

The results of this benchmark parameterisation are shown in Figure 2, with distance from the CBD as the bottom axis of each panel.^[4] Based on households' preferences for proximity to the CBD, land is priced more highly closer to the city centre and declines as one moves further from the CBD (bottom left panel). Accordingly, building firms and households economise on the use of well-located land. As a result, building height is higher closer to the centre (middle left panel) and dwelling size is smaller (upper right panel). An implication is that population density rises sharply closer to the CBD (middle right panel). Housing prices (per unit of living space) are naturally also higher closer to the CBD (upper left panel), with lower housing prices and larger dwelling sizes providing the incentive for some households to live further from the CBD. Finally, the particular distance at which home-builders and households no longer value land more highly than agricultural users corresponds to the city boundary, around 35 kilometres in this calibration. Given the city population and density at different distances to the city, we calculate a curve (lower right panel) that shows, at every distance from the CBD, the number of residents that reside up to that location.

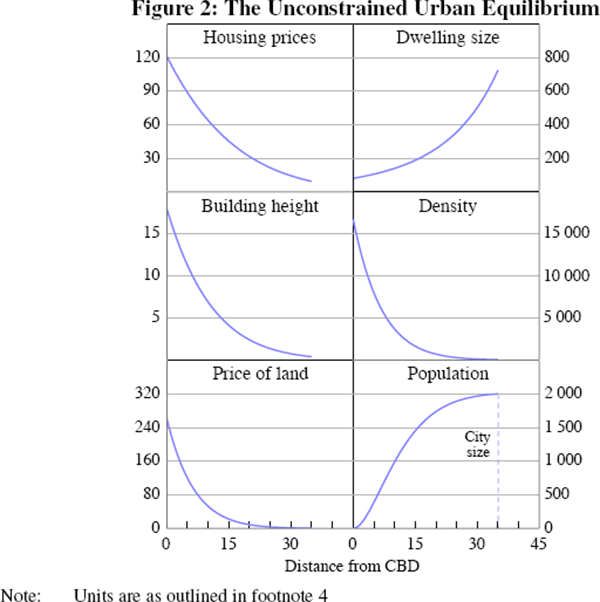
We take this parameterisation as a benchmark; it is not an attempt to fit particular features of the data. In the benchmark calibration, population density, for example, seems high close to the city centre: around half the population lives within ten kilometres of the centre, which is higher than is the case of the five largest Australian cities. Of course, if policies to limit density are binding in reality or if cities have multiple business centres, calibrating an unconstrained monocentric model will, not surprisingly, suggest higher density close to the city centre than is observed in reality. Similarly, given that real-world cities grow gradually and housing structures are long-lived, it should not be surprising if actual cities are geographically larger than the equilibrium suggested by a model which abstracts from these sort of adjustment costs. Having said this, we use this calibration as an initial benchmark against which to assess the impact of various policies and the impact of population growth.

Footnotes

We discuss the ‘closed-city’ version of the model which takes the population as exogenous. An ‘open-city’ version allows for migration flows, in which case the city's population is determined endogenously. See also Brueckner (1987) and Anas, Arnott and Small (1998) for survey articles on the model and various extensions. [1]

See Spivey (2008), for a recent test of the model using data for US cities. [2]

This 15 per cent figure broadly matches the average for all households in the 2005/06 ABS Household Expenditure Survey; in reality, younger households spend a greater fraction than this average, while older households spend less. [3]

As noted in the text, the parameterised model should not be expected to fit all dimensions of any particular city. The units of this figure and subsequent ones are as follows: housing (rental) prices in dollars per square metre of living space per year; dwelling size in square metres of living space; building height in housing floor space per unit of land, which corresponds roughly to stories; density in persons per square kilometre; (rental) price of land in thousands of dollars per hectare per year; and population in thousands. The model refers to the rental price of housing and land, but under an assumption of a given capitalisation rate, these translate directly to purchase prices, which we refer to in our discussion. [4]