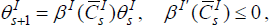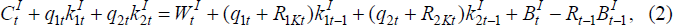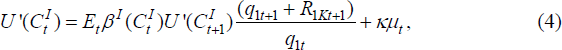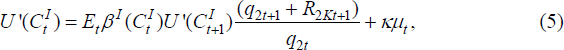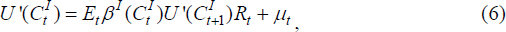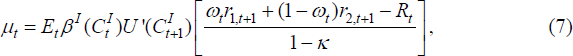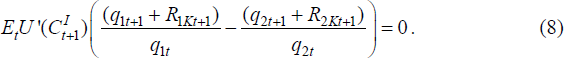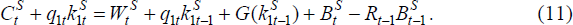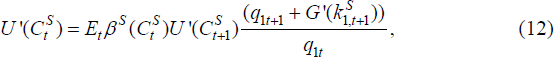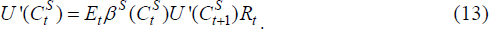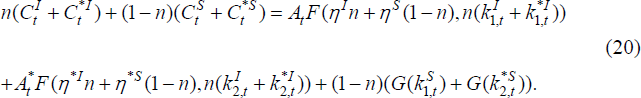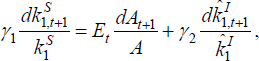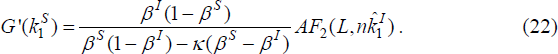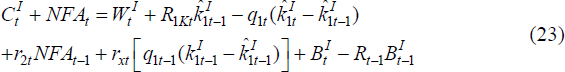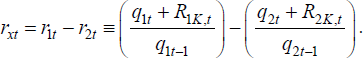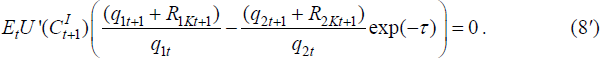RDP 2009-08: Leverage Constraints and the International Transmission of Shocks 3. The Model
December 2009
- Download the Paper 252KB
In this section we describe a basic two-country model with levered borrowers and lenders in each country. The countries are called home and foreign. Within each country there are investors and savers, both of whom have infinite horizons and use the same fixed asset in production (with no capital accumulation, this is literally in fixed supply). Investors purchase the fixed asset and rent it to production firms, receiving a risky return in exchange. We may think of this investment as the purchase of an equity claim in the production firm. Investors are more impatient than savers, so they will borrow from savers in order to invest in the fixed asset.[5] Savers also make use of the fixed asset in home production. Savers therefore choose a portfolio in which they hold the debt of investors and the fixed asset. By assumption, savers do not hold domestic or foreign equity. In the current version, we assume that savers do not lend to foreign investors. Because the model is symmetric, this makes little difference for the results.
Investors in either country, however, may trade claims with investors in the other country so as to diversify their portfolio of equity holdings. Thus investors in each country hold levered investments, but also have equity portfolios that are interconnected across countries. Finally, both investors and savers in each country supply labour inelastically to production firms.
3.1 Investors
We normalise the population of each country to unity, with a measure n of investors and 1−n savers. The representative investor in the home country maximises:
where 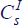 is consumption of the final good. To keep the analysis focused solely on financial
linkages between countries, it is assumed that there is just one world good.
Adding an endogenous terms of trade to the analysis would enrich the response,
but would not fundamentally alter the cross-country transmission of balance
sheet adjustments modelled here, so long as the elasticity of substitution
across home and foreign goods is not close to
unity.[6]
is consumption of the final good. To keep the analysis focused solely on financial
linkages between countries, it is assumed that there is just one world good.
Adding an endogenous terms of trade to the analysis would enrich the response,
but would not fundamentally alter the cross-country transmission of balance
sheet adjustments modelled here, so long as the elasticity of substitution
across home and foreign goods is not close to
unity.[6]
We define the discount factor for investors such that:
where 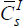 is the economy-wide average consumption of investors. Thus the investor's time
preference is increasing in consumption, but the rate of time preference is
taken as given by the individual investor. The assumption of endogenous time
preference for investors plays the usual role of ensuring a stationary distribution
of wealth among groups, both within countries and across countries. But it
also plays a key role in allowing for a comparison of an economy in which
financial constraints bind with one where they do not bind, as we discuss
below.
is the economy-wide average consumption of investors. Thus the investor's time
preference is increasing in consumption, but the rate of time preference is
taken as given by the individual investor. The assumption of endogenous time
preference for investors plays the usual role of ensuring a stationary distribution
of wealth among groups, both within countries and across countries. But it
also plays a key role in allowing for a comparison of an economy in which
financial constraints bind with one where they do not bind, as we discuss
below.
Investors receive income from their current holdings of domestic and foreign equity, as well as labour income from working in the domestic production firm. In addition, they must repay their debts owed to domestic savers. They then issue new debt, purchase equity claims on home and foreign assets/capital and consume. The home country investor's budget constraint is written as:
where: q1t and q2t represent the price of
the fixed asset (or equity) in the home and foreign country, respectively;
and 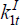 and
and 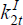 are the portfolio holdings of the fixed assets in each country held by the home
investor. The fixed asset of the home (foreign) country earns a return of
R1Kt
(R2Kt).
are the portfolio holdings of the fixed assets in each country held by the home
investor. The fixed asset of the home (foreign) country earns a return of
R1Kt
(R2Kt). 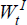 is wage income for
the investor, who supplies one unit of labour. Finally,
is wage income for
the investor, who supplies one unit of labour. Finally, 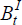 is the debt issued
to domestic savers and
is the debt issued
to domestic savers and 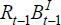 is payment on previously incurred debt.
is payment on previously incurred debt.
One may question why only investors can purchase the fixed assets, which are then used by final goods firms. As in Bernanke et al (1999), we could assume that investors (or, in their model, entrepreneurs) have some special capability for transforming a unit of the fixed asset into a usable factor of production that is rented to production firms. Lenders cannot do this, and so may gain only indirectly from the investment, by lending to the investors.
In addition to Constraint (2), we assume that investors face a constraint on total leverage due to an inability to commit to repayment, as in Kiyotaki and Moore (1997). Total debt is assumed to be restricted to be no greater than κ times the market value of equity assets, where κ<1. Thus home investors' choices are constrained by:
The full leverage rate (the value of assets to capital) for investors is then 1/(1 − κ) in the case where the Leverage Constraint (3) is binding. We take κ as a free variable in our analysis. Leverage constraints of this form have been used quite widely in the literature on asset prices (Aiyagari and Gertler 1999), emerging market crises (Mendoza and Smith 2006), borrowing in a small open economy (Uribe 2006) and monetary policy with credit frictions (Iacoviello 2005). Kiyotaki and Moore (1997) show that κ may depend on the borrowing rate and expected capital gains on equity under some circumstances.
Investors in the home country choose investment in home equity and foreign equity, as well as borrowing, to maximise their expected utility subject to their Budget Constraint (2) and Leverage Constraint (3), which implies:
where μ is the multiplier on the leverage constraint, or equivalently the utility benefit of an extra unit of debt to the investor. If this is positive, it means that the investor would like to borrow more, but is constrained by Equation (3). Therefore current marginal utility is less than expected future (discounted) marginal utility times the return on investing in either the home or foreign country. Thus μ is a measure of the value of the opportunity to make a levered investment. To show this, put Equations (4), (5) and (6) together to obtain:
where: ωt=q1,tk1,t/(q1,tk1,t + q2,tk2,t) is the share in home equity; r1,t+1=(q1,t+1 + R1K,t+1)/q1,t is the return on the home equity; and r2t+1 = (q2,t+1 + R2K,t+1)/q2,t is the return on the foreign equity. Equation (7) shows that, for a given distribution of excess returns and consumption, μ is higher the higher is the leverage rate. It also implies that, when μ > 0, the expected return on the portfolio, up to the first-order, exceeds the cost of borrowing.
Note that the leverage constraint does not directly affect the investors' incentive to diversify equity holdings across countries, since Constraint (3) applies equally to borrowing for domestic or foreign equity purchases. Thus we may put Equations (4) and (5) together to get the standard portfolio selection condition:
Given that the portfolio choice may be written in the form of Equation (8), we can use the recent methods described in Devereux and Sutherland (forthcoming) to derive the optimal equity portfolio of each country's investors. This involves using a second-order approximation of Equation (8) in conjunction with a linear approximation of the remaining aspects of the model. We discuss the details involved in portfolio choice more fully below.
3.2 Savers
Savers have preferences given by:
Again, as for investors, we define the discount factor such that 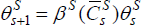 ,
with
,
with 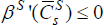 ,
where
,
where 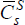 ,
is the economy-wide aggregate consumption of savers. We make the assumption
that savers are inherently more ‘patient’ than investors in the
sense that:
,
is the economy-wide aggregate consumption of savers. We make the assumption
that savers are inherently more ‘patient’ than investors in the
sense that:
for all feasible values of x. Assumption (10) ensures that savers will lend to investors, even in a steady state where the Leverage Constraint (3) is not binding.[7]
Savers purchase the fixed asset and buy debt from investors. They receive wage income
from working in the final goods sector, and returns on their lending to investors.
In addition, they have a residual ‘home production function’ that
uses the fixed asset. Thus an individual saver owning 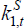 of the fixed asset produces
of the fixed asset produces 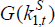 in terms of home production, where
in terms of home production, where 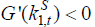 .
For simplicity, we assume that home production is perfectly substitutable
with the final good in savers' preferences. With this assumption, we may
write the saver's budget constraint as:
.
For simplicity, we assume that home production is perfectly substitutable
with the final good in savers' preferences. With this assumption, we may
write the saver's budget constraint as:
Note that, by assumption, savers can purchase the domestic fixed asset, but not the
foreign fixed asset. (As is made clear below, if investors are in debt, 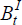 > 0, then
> 0, then 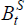 < 0; see Equation (19).) They do not have access to the same investment opportunities
as investors and therefore only have use for the domestic fixed asset, as
it may be utilised in home production. On the other hand, savers' purchases
of debt from investors are unconstrained.
< 0; see Equation (19).) They do not have access to the same investment opportunities
as investors and therefore only have use for the domestic fixed asset, as
it may be utilised in home production. On the other hand, savers' purchases
of debt from investors are unconstrained.
The first-order conditions for the optimal choice of 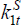 and
and 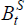 are simply:
are simply:
3.3 Production Firms
Production firms in each country hire capital and fixed assets in order to produce. Firms are competitive, and maximise profits given the production function:
where Lt is effective employment and Kt
is the firm's use of the fixed asset. We allow for labour supplied by
investors and savers to have different fixed productive content. Thus 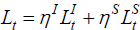 ,
where ηI
and ηS are fixed effective productivity factors. Profit
maximisation then implies that:
,
where ηI
and ηS are fixed effective productivity factors. Profit
maximisation then implies that:
3.4 Equilibrium
Equilibrium of the two-country world economy entails market clearing for the world market of the fixed asset, as well as each country's debt market. Thus, for the home economy, it must be the case that:
where 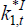 represents foreign country investors' real holdings of the home asset at the
beginning of time t + 1. In addition, the world market clearing condition
must be satisfied:
represents foreign country investors' real holdings of the home asset at the
beginning of time t + 1. In addition, the world market clearing condition
must be satisfied:
This condition incorporates the fact that the total labour supply of investors and
savers is n and 1-n respectively, and total use of the fixed factor
by final goods firms is equal to total holdings by domestic and foreign investors.
The full equilibrium is then described by Equations (2)–(6) and (11)–(19)
for both the home and foreign country, and the world market clearing Condition
(19). This gives 27 equations in the 26 variables 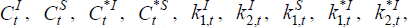
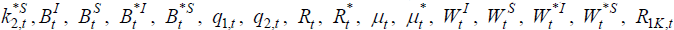 and
and 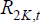 ; one equation is redundant
given Walras' law.
; one equation is redundant
given Walras' law.
3.5 Properties of the Steady State
Before examining the dynamics of balance sheet adjustments within the model, we first discuss some properties of the non-stochastic steady state. This is particularly easy in the case of μ = μ* = 0, which is when leverage constraints do not bind. It then follows from a combination of Equations (4) and (6), together with Equations (12) and (13), that the fixed asset is allocated efficiently between the final good sector and home production. That is, for the home economy, we have:
where 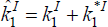 represents the total quantity of the fixed asset used in the final goods production
sector. Thus the fixed asset is allocated efficiently in the sense that its
marginal product is equalised between home production and final goods production.
represents the total quantity of the fixed asset used in the final goods production
sector. Thus the fixed asset is allocated efficiently in the sense that its
marginal product is equalised between home production and final goods production.
In combination with the Resource Constraint (17), 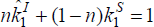 ,
this uniquely determines the allocation of assets in final goods production.
Therefore there is no interdependence across countries in asset allocation
in steady state when leverage constraints do not bind. Hence output levels
are independent across countries – a permanent increase in productivity
A affects home output, but not foreign output.
,
this uniquely determines the allocation of assets in final goods production.
Therefore there is no interdependence across countries in asset allocation
in steady state when leverage constraints do not bind. Hence output levels
are independent across countries – a permanent increase in productivity
A affects home output, but not foreign output.
In fact, we can extend this result further. In the case where leverage constraints never bind, it is easy to see that there is no interaction between asset allocations across countries at all, at least up to a first-order approximation. This can be seen by taking a linear approximation of Equations (4), (6), (12) and (13) to obtain the condition:
where γ1 and γ2 are constant coefficients. Hence the dynamic paths of asset allocations are independent across countries in the absence of balance sheet constraints.[8] Note that this holds despite the fact that, up to a first-order, expected returns on all assets are equalised both within and across countries.
A more general feature of this environment is that portfolio holdings have no feedback effect on asset allocations. That is, allocation of the fixed asset between home production and investment in the final good is independent of the ownership of equities. This property will not hold in an economy with binding leverage constraints.
When leverage constraints bind, we again use Equations (4), (6), (12) and (13) to obtain the steady-state condition:
From Condition (3), because investors face a higher cost of finance, it must be true that βI(1−βS)/[βS(1−βI)−κ (βS−βI)]<1 so it follows that, under binding leverage constraints, the final goods sector has an inefficiently low level of the fixed asset. More generally, however, since discount factors are endogenous, the allocation of fixed assets across sectors will no longer be independent across countries. Asset allocation in the home country will depend on the level of productivity in the foreign country. Intuitively this holds because, with free trade in equities across countries, returns to investors must be equal in both countries. Since returns interact with movements in consumption through the endogenous rate of time preference, Equation (22) shows that the division of resources between home production and final goods must be linked across countries as well. It therefore follows that, unlike the case in which leverage constraints are not binding, the cross-country ownership of equity holdings will in general have implications for the allocation of investment in fixed assets.
Even in the case of constant time preferences, however, the presence of leverage constraints would still imply a dynamic interaction between output levels across countries that is absent without these constraints, because productivity shocks to one country will affect the tightness of leverage constraints across all financial markets. We explore this in detail below.
3.6 Portfolio Choice
We have already solved for the overall allocation of the fixed asset in each country
in steady state, but not the ownership structure of equities. Thus, while
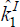 is determined by Equations (21) or (22) with non-binding or binding leverage constraints
respectively,
is determined by Equations (21) or (22) with non-binding or binding leverage constraints
respectively, 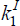 and
and 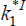 are not yet determined.
Clearly, in order to analyse the dynamic response to productivity shocks in
one country, it is necessary to understand the structure of equity holdings.
To do this, we follow Devereux and Sutherland (forthcoming) in using a second-order
expansion of Equation (8) to obtain an approximation of optimal portfolio
holdings.
are not yet determined.
Clearly, in order to analyse the dynamic response to productivity shocks in
one country, it is necessary to understand the structure of equity holdings.
To do this, we follow Devereux and Sutherland (forthcoming) in using a second-order
expansion of Equation (8) to obtain an approximation of optimal portfolio
holdings.
Since only investors have access to equity markets by assumption, it is sufficient to look at the portfolio decisions of home and foreign investors. To illustrate the application of Devereux and Sutherland (forthcoming) to the present model, take the Budget Constraint (2) for home country investors. This may be rewritten as:
where NFAt denotes net foreign assets, defined as 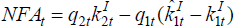 , and rxt
is the excess return on the portfolio:
, and rxt
is the excess return on the portfolio:
For given NFAt, the portfolio choice may be described as the choice
of 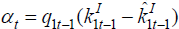 ,
which is the negative of the holding of home equity by foreign investors.
If
αt < 0, the investors are diversified in the
sense that less than 100 per cent of all home equity is owned by home investors.
Devereux and Sutherland (forthcoming) show that, when the model is analysed
up to a first-order approximation, αt is a constant
and is determined by a combination of a second-order approximation of Equation
(8), together with a first-order approximation of the rest of the model.
,
which is the negative of the holding of home equity by foreign investors.
If
αt < 0, the investors are diversified in the
sense that less than 100 per cent of all home equity is owned by home investors.
Devereux and Sutherland (forthcoming) show that, when the model is analysed
up to a first-order approximation, αt is a constant
and is determined by a combination of a second-order approximation of Equation
(8), together with a first-order approximation of the rest of the model.
In the solution below, following Tille and van Wincoop (2007), we extend Equation (8) to allow for transactions costs of international financial trade that effectively limit international portfolio diversification. This represents a brute-force technique for generating an equilibrium with home equity bias. In particular, we assume that an ‘iceberg’ cost factor given by exp(−τ)≤1 reduces the returns that home investors receive from foreign investment so that Condition (8) becomes:
In addition, we follow Tille and Van Wincoop in assuming that τ is a small, second-order term. This means that while it does affect the solution for the equilibrium portfolio, which is evaluated using a second-order approximation of Equation (8'), it does not affect the first-order dynamics of the model, except insofar as it affects the choice of the portfolio itself.
Note that given the definition of net foreign assets (NFA), the leverage constraint for home country investors becomes:
Thus, holding home asset prices constant, an increase in net foreign assets generated by either a current account surplus or a capital gain on the external portfolio will loosen the leverage constraint. But since NFAt + NFAt* = 0, this will simultaneously tighten the leverage constraint facing foreign investors. Thus the degree to which leverage linkages govern the transmission of shocks across countries depends on the dynamics of net foreign assets, and these in turn are linked to the portfolio choices made by home and foreign investors.
3.7 Calibration
Because the model is such a stripped-down representation of a full-scale DSGE framework, lacking capital accumulation and dynamics in the supply of labour, and containing only a single world good, there are many dimensions in which the model's predictions will depart from reality. The aim of the exercise is solely to explore the way in which financial leverage constraints affect the cross-country dynamics of asset prices, asset allocations and levered investments, and to investigate the international transmission of balance sheet contractions. To do this we need to choose parameter values for preferences, production technologies and the leverage constraint itself. Table 3 gives the set of parameter values used in the baseline model.
| Parameter | Description | Value |
|---|---|---|
| n | Share of investors | 0.5 |
| ηI, ηS | Effective labour productivity | 1 |
| Discount factors are 0.96 and 0.94 for investors and savers, respectively (according to parameter ζ ) |
||
| η | Discount factor parameter | 0.01 |
| κ | Leverage constraint | 0.5, 0.8 |
| ε | Cobb Douglas production | 0.5 |
| ω | Home production | 0.36 |
| σ | Risk aversion | 5 |
| ρ | Productivity shock persistence | 0.9 |
We assume that the measure of investors and savers is equal, so that n = 0.5. In the leverage-constrained economy, this accords with the estimates of Campbell and Mankiw (1990) regarding the share of households that are subject to credit constraints in the US economy.
We assume a discount factor defined as:
We set η = 0.01, and choose ζ so that, in a steady state
with binding leverage constraints, lenders and borrowers have discount factors
of 0.96 and 0.94 respectively. The parameter κ directly determines
the total value of assets that investors can borrow. Since the model is calibrated
in a symmetric way, net foreign assets are zero in steady state so that home
investors' net worth, measured as total assets less debt, equals 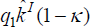 (and similarly,
(and similarly, 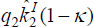 for foreign investors).
for foreign investors).
Total leverage (investment relative to capital) is equal to 1/(1−κ). This leverage ratio has a significant effect on the model's dynamics quantitatively. We examine two alternatives. First, in response to the discussion of the high rates of leverage seen in the financial system in recent years we explore the implications of a relatively high leverage ratio of 5 (κ = 0.8). Second, we also consider a relatively low leverage ratio of 2 (κ = 0.5), as in Bernanke and Gertler (1999). From a qualitative point of view, we will see that the results are very similar for both leverage ratios.
We assume a Cobb-Douglas final goods production technology, and let F(L,K) = LεK1−ε. In order to have substantial propagation effects from leverage constraints, Kiyotaki and Moore (1997) require that production in the borrowing sector is linear in the fixed asset. Kocherlakota (2000) shows that, with a more conventional calibration allowing for decreasing returns, credit constraints have much less impact. We set ε = 0.5, implying substantial decreasing returns, yet find substantial effects of leverage constraints, as we will see. Our choice of ε implies that fixed assets are slightly more important than conventional measures of capital's share in calibrations of the US economy.[9] In addition we assume that effective labour productivity of savers and lenders is initially equal, so that ηI = ηS = 1.
Regarding the home production sector, we assume that 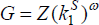 and ω = 0.36, implying that the fixed asset is less important in
this sector, consistent with convention. We set A = Z =
1 in steady state. The combination of these assumptions implies that, in steady
state, 80 per cent of the fixed asset is employed in final goods production.
We follow the asset pricing literature (see, for example, Bansal and Yaron
2004) in setting a relatively high degree of risk aversion with σ
= 5 in U(C) = C1−σ/(1−σ).
Lower values of σ reduce the volatility of asset prices, but
have little qualitative effect on the results otherwise.
and ω = 0.36, implying that the fixed asset is less important in
this sector, consistent with convention. We set A = Z =
1 in steady state. The combination of these assumptions implies that, in steady
state, 80 per cent of the fixed asset is employed in final goods production.
We follow the asset pricing literature (see, for example, Bansal and Yaron
2004) in setting a relatively high degree of risk aversion with σ
= 5 in U(C) = C1−σ/(1−σ).
Lower values of σ reduce the volatility of asset prices, but
have little qualitative effect on the results otherwise.
We focus on shocks to the productivity of final goods in each country. The stochastic process for final goods productivity is modeled as:
where ρ = 0.9, Et−1νt
= 0 and 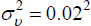 .
We assume that foreign productivity is driven by the same process, and foreign
and domestic productivity shocks are uncorrelated.
.
We assume that foreign productivity is driven by the same process, and foreign
and domestic productivity shocks are uncorrelated.
Footnotes
Because they are more impatient than savers, investors will never accumulate enough resources to cover the cost of investment in any period. [5]
As is well known, with an elasticity of substitution equal to unity, there is a high cross-country correlation of consumption purely due to the risk-sharing implications of terms of trade adjustment. This is seen, for instance, in the paper by Dedola and Lombardo (2009). Aghion, Bacchetta and Banerjee (2004) explore the importance of terms of trade movements in affecting borrowing constraints in an emerging market economy framework. Extending our model to a setting with endogenous terms of trade would affect borrowing constraints through the impact of an adjustment of the terms of trade on net worth in a similar way to the effects of asset price changes in the present version of the model. [6]
An alternative, but considerably more difficult, approach to achieving an equilibrium with levered investment is to assume that investors are less risk averse than savers. Solving a model with leverage based on risk preferences would be substantially harder than the approach we follow, because we would need to solve the full stochastic model to a higher order of approximation. [7]
Of course this is not a robust feature, and would be altered in a model with endogenous labour supply or capital accumulation. But the main point here is to show that the presence of balance sheet constraints introduces substantial additional forces for cross-country correlations that would otherwise be absent. [8]
For many emerging market economies, however, estimates of capital share equal to 50 per cent are quite common. [9]