RDP 2009-08: Leverage Constraints and the International Transmission of Shocks 4. Effects of Productivity Shocks
December 2009
- Download the Paper 252KB
In this section we look at how the combination of balance sheet constraints with portfolio interdependence affects the model's response to a productivity shocks in one country. The focus on a productivity shock is not of central importance. The main elements of the propagation mechanism hold also for other shocks. The key aspect of the model is to show that the two features of portfolio interdependence and balance sheet constraints introduce a substantial process of macroeconomic co-movement that is absent when these features are not present.
4.1 No Leverage Constraints
We first examine the impact of a 1 per cent adverse productivity shock in the home
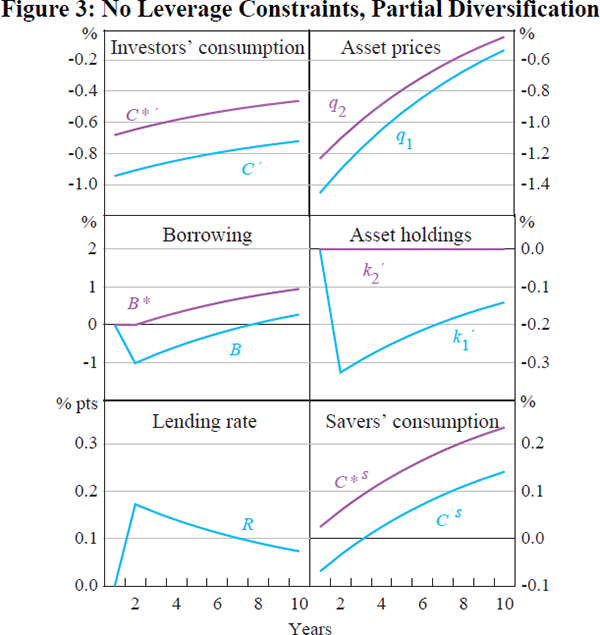
country, in the environment without leverage constraints. Figures 3 and 4
describe the impact of the shock on consumption of investors, asset prices,
lending by savers, asset allocation, the internal lending rate and the consumption
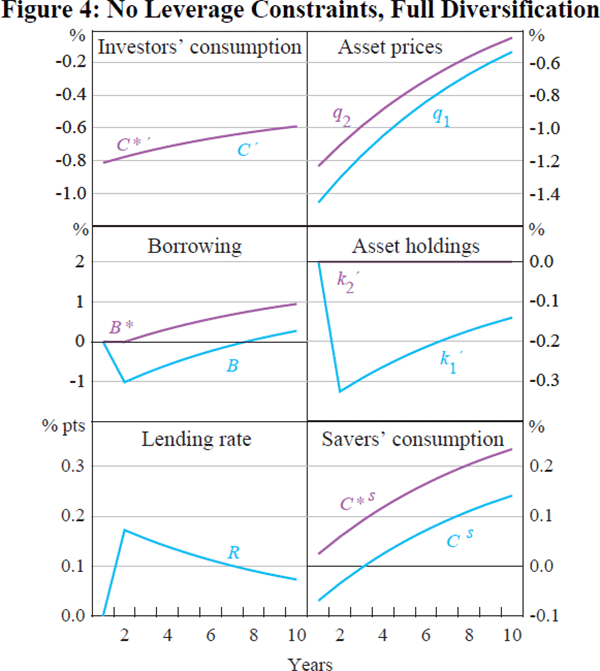
of savers. Figure 3 represents the case where portfolio diversification is
restricted by second-order transactions costs as described above, while Figure
4 describes the case of unrestricted portfolios. In the unrestricted case,
investors in the home country choose values for 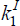 and
and 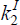 to satisfy Equation (8'), evaluated up to second-order, with τ
= 0. This involves home investors having a bias against home equities.
This reflects the fact that investors are exposed to non-diversifiable risk
from wage income, which is positively correlated with the return on home equity.
With an unrestricted portfolio, they will hedge this risk by taking a larger
position in foreign equity than home equity, as discussed in Baxter and Jehrmann
(1997). Given the calibration of the model, in an unrestricted equilibrium
to satisfy Equation (8'), evaluated up to second-order, with τ
= 0. This involves home investors having a bias against home equities.
This reflects the fact that investors are exposed to non-diversifiable risk
from wage income, which is positively correlated with the return on home equity.
With an unrestricted portfolio, they will hedge this risk by taking a larger
position in foreign equity than home equity, as discussed in Baxter and Jehrmann
(1997). Given the calibration of the model, in an unrestricted equilibrium
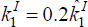 .
That is, home investors would hold only 20 per cent of total home equity (that
is, 20 per cent of the fixed assets which are invested in the home final goods
technology), with foreign investors holding the remaining 80 per cent.
.
That is, home investors would hold only 20 per cent of total home equity (that
is, 20 per cent of the fixed assets which are invested in the home final goods
technology), with foreign investors holding the remaining 80 per cent.
Since this is clearly counterfactual, we use the iceberg cost variable τ as a crude mechanism to match the optimal portfolios more closely
with observed home bias in equity holdings. In Figure 3, τ has
been chosen so that 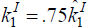 , implying that home investors hold 75 per
cent of home equity. Figure 4, by contrast, illustrates the counterfactual
case where there is full consumption risk-sharing for investors due to unrestricted
diversification.
, implying that home investors hold 75 per
cent of home equity. Figure 4, by contrast, illustrates the counterfactual
case where there is full consumption risk-sharing for investors due to unrestricted
diversification.
The responses to a productivity shock are quite similar in each of the figures. Without leverage constraints, the impact of a fall in home country productivity is to reduce consumption of investors in both countries, by identical amounts in the case of unrestricted diversification. The shock represents a temporary fall in consumption. Since consumption is expected to increase in the future, real interest rates must rise. The combination of a lower return on the home asset and rising real interest rates means that the home asset price must immediately fall.
Without leverage constraints, all returns are equalised, at least up to a first-order approximation, in order for investors to be willing to hold all assets in their portfolios. Thus the price of foreign assets must also fall. That is, arbitrage implies that the rate of return to lenders rises by the same amount in both countries, even though lenders do not directly engage in international borrowing or lending. But the pattern of lending moves in different directions in the two countries, as do lenders' portfolios. In the home country, there is a fall in investment in the fixed asset in the final goods sector simply because this sector has suffered a persistent negative technology shock. This leads to an increase in the holdings of the fixed asset by lenders. They shift the composition of their portfolios from debt towards increased holdings of the fixed asset. Thus lending falls in the home country. In the foreign country, by contrast, there is no change at all in the allocation of the fixed asset. But lending in the foreign country actually rises, as investors borrow more from lenders in order to cushion against the temporary fall in their investment income.
A different way to see this is that in the foreign country, lenders are offered a higher rate of return on their lending, and are willing to purchase more debt from foreign investors. Either way we look at it, lending rises in the foreign country, while it falls in the home country. In this sense, there is no international transmission of balance sheet contractions.
The impact of the shock on lenders' consumption in the two countries also moves in opposite directions. Lenders in the home country lose, since they suffer a direct fall in their wage income. Lenders in the foreign country gain, since they lend more at higher interest rates, and their wage income and holdings of the fixed asset are unaffected. Clearly lenders cannot achieve full consumption risk-sharing, since they cannot directly hold a claim on the equity of the other country.
In the economy without leverage constraints, then, the international transmission of shocks is limited, and clearly counterfactual, relative to the discussion of the empirical evidence of financial spillovers in Section 2. A negative productivity shock in the home country leads to balance sheet contractions domestically, as investors reduce both their borrowing and holdings of fixed assets. But there are no foreign balance sheet contractions. Investment in fixed assets is completely unaffected in the foreign country, and foreign investors actually increase their borrowing. More critically, there is no international transmission of the shock to GDP at all. Since the foreign asset allocation is unaffected by the domestic shock, foreign output is unchanged. Thus, in the absence of credit market imperfections, the possibility for the international transmission of shocks through balance sheet contractions is limited.
4.2 Leverage Constraints and International Transmission
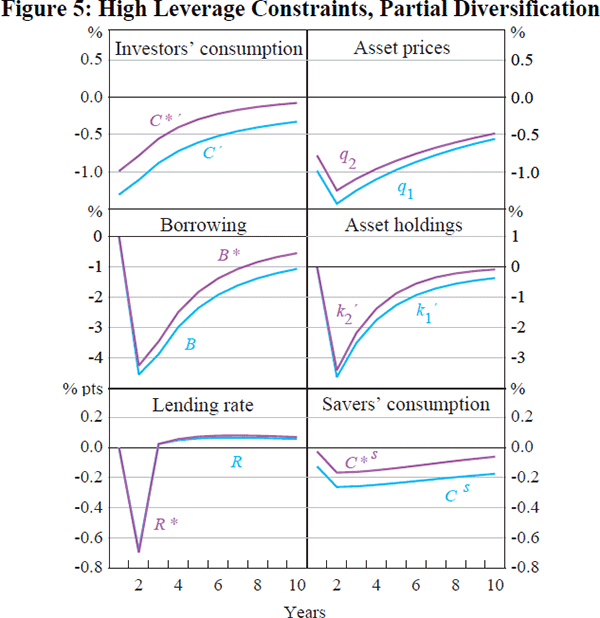
Figures 5–8 show the impact of a negative productivity shock in the home country for the case when leverage constraints bind in both countries. Figures 5 and 6 illustrate the case where the leverage ratio (LR) is relatively high at 5 – that is, the constraint is relatively ‘loose’; for Figure 5 investors' portfolios are only partly diversified due to the presence of transactions costs while Figure 6 shows the case of unrestricted portfolio diversification.
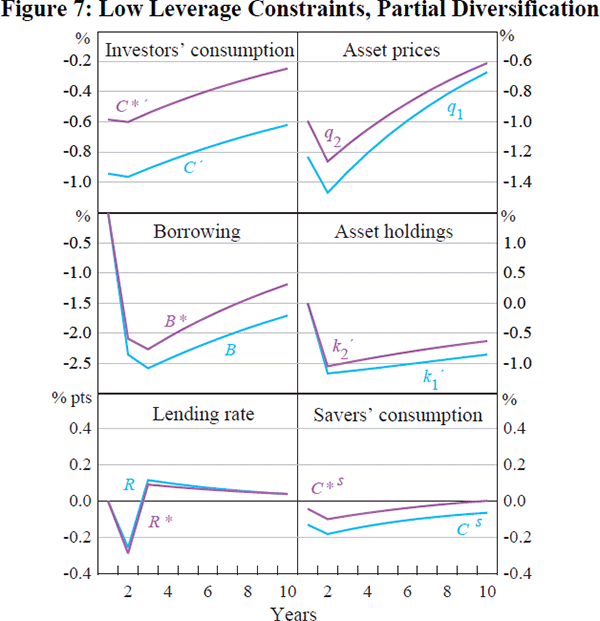
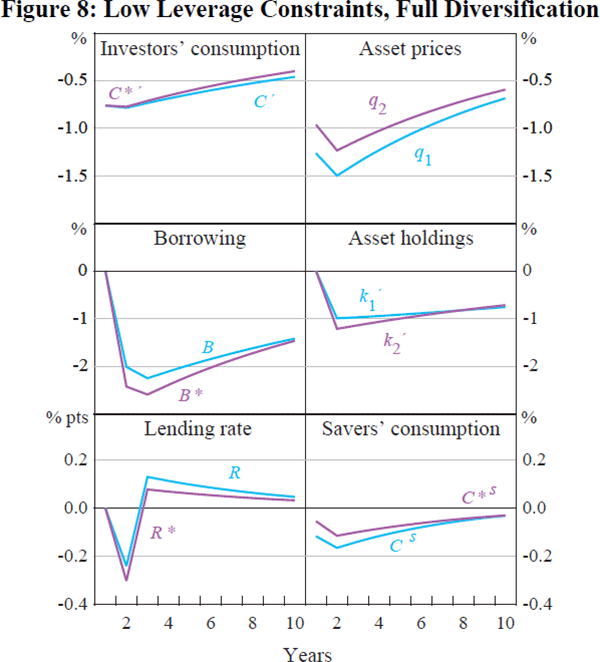
Figures 7 and 8 illustrate the case where leverage is at a lower ratio of 2 – in the case of partial and full portfolio diversification respectively. In all cases there is a clear pattern of global balance sheet contractions in response to the shock.
With high leverage and unrestricted portfolios (Figure 6), the home investor wishes to hold only 47 per cent of total home equity. While there is still some bias towards foreign equity, it is far less than in the economy without leverage constraints. That is, in an equilibrium without portfolio transactions costs, investors wish to hold more of their own equity when there are leverage constraints than when there are not. The reason is that the transmission of balance sheet contractions across countries with binding leverage constraints will make equity returns more positively correlated, as we see below. As a result, the gains from equity diversification are lessened. In Figure 5 we calibrate τ so that investors hold 75 per cent of domestic equity, as in Figure 3.
Without leverage constraints (as in Section 4.1), the fall in home country productivity leads to a fall in asset prices in both countries, and a fall in investors' consumption. But now the fall in asset prices leads to a tightening of the leverage constraint, both in the home and foreign countries. The result is a reduction in borrowing by investors in both countries, and a consequent reduction in investment in fixed assets. Note that, for the foreign country, there is no direct fall in the productivity of the domestic final goods sector. The fall in investment takes place purely through balance sheet linkages.
In addition, the price of foreign equity falls. But in spite of there being no direct shock to future return R2K,t+1, and a fall in the price of the asset, there is still a fall in demand for the asset by investors in both countries. This is the essence of the ‘inverted demand curve’ for assets that characterises episodes of balance sheet contractions, emphasised by Aiyagari and Gertler (1999). Here it is taking place as a spillover from one levered investor to another, as emphasised by Krugman (2008). That is, a fall in the price of the asset held by one investor leads to a tightening of leverage constraints and a fall in demand for both the original asset and other assets held in the portfolio.
Even in the case where portfolios are only partly diversified, there is a very high correlation across countries in borrowing and investment. The balance sheet contraction is so great that the internal lending rate in each country immediately falls. Again, note that this is in response to a temporary shock so that future consumption of investors is expected to increase. But because investors are subject to leverage constraints, the path of their consumption is de-linked from the path of interest rates. To see this more clearly, note from Equation (6) that there is a conflict between the Fisherian determinants of real interest rates and the effect of binding leverage constraints. Since consumption falls for both home and foreign investors, but is expected to rise in the future, real interest rates should rise. But this effect is more than offset by the increase in the shadow price of borrowing due to the leverage constraint. The fall in asset prices leads to such a large balance sheet contraction in both countries, and correspondingly a large rise in the shadow price of borrowing, that the real interest rate offered by lenders falls (at least in year 2) rather than rises.
The fall in asset prices is of a similar order of magnitude in the leverage-constrained economy as in the unconstrained economy. Asset prices display a V-shaped response, however, falling further in the second year than in the first. This is due to the fall in lending rates. Since lenders are unconstrained, the fall in returns on lending must be accompanied by a fall in the expected returns for lenders holding fixed assets for home production. Hence, immediately following the shock, asset prices are expected to fall further.
Note that there is a distinct difference between the constrained and unconstrained economy, not just in the direction of the international transmission of shocks, but also in the scale. In the unconstrained economy (with partial diversification), a 1 per cent decline in final goods' sector productivity leads to an approximately 1 per cent fall in borrowing from lenders, but only a 0.3 per cent reduction in fixed asset investment. Not only is there an absence of international transmission via balance sheet contractions, but the domestic impact of the shock is also relatively mild. By contrast, the response of the constrained economy is larger by orders of magnitude. Borrowing falls by almost 5 per cent in the home economy and investment in fixed assets by almost 4 per cent. Even in the foreign economy, the multiplied effect of the shock is very large – investment falls by over 3 per cent and borrowing by 4 per cent. In both countries, the response to the shock is proportionally much larger than the shock itself, due to the interaction of asset price declines and binding leverage constraints.
Consumption of home and foreign investors also falls by more in the constrained economy than in the unconstrained economy, although the decline is less persistent with leverage constraints. Also, in contrast to the economy without constraints, consumption falls for all categories of households, both for investors and lenders, in both countries. The fall in interest rates on lending in the foreign country eliminates the positive wealth effect we saw foreign lenders receive in the unconstrained economy.
When portfolio diversification is unrestricted, Figure 6 shows that the international transmission of the shocks is heightened even more. In fact, we get the surprising prediction that the size of the balance sheet contraction and disinvestment is greater in the foreign country than in the home country! Borrowing falls by 5 per cent in the foreign economy, and investment 4 per cent, while the equivalent reductions in the home economy are 4 per cent and 3.5 per cent respectively.
Why does greater portfolio diversification magnify the international propagation effects of the shock? The reason is clear from the Leverage Constraints (3) or (23). Increased diversification leads to a greater sensitivity of foreign balance sheets to the domestic asset price, and therefore a larger balance sheet contraction in response to a negative shock to home productivity. In the completely unrestricted portfolio equilibrium (when τ = 0), the foreign country is over-weighted in home equity, as part of an optimal risk sharing arrangement. So the macroeconomic reverberations of the shock are greater in the foreign country than the domestic country, despite the fact that the actual shock takes place only in the home economy. Thus the ownership pattern of equity holdings, and its consequent implication for balance sheet constraints in this case, are more important for the business cycle response than is the geographical source of macro shocks.
A second important feature of Figure 6 is that full portfolio diversification cannot ensure full consumption risk-sharing in the leverage-constrained economy, unlike the case of an economy without leverage constraints. This is because the evolution of domestic interest rates, and hence the domestic debt burden facing investors, is no longer identical across the two countries. Since equity market diversification cannot diversify risk associated with country-specific interest rate movements, unrestricted equity market integration (that is, when τ = 0) no longer achieves full consumption risk-sharing in response to productivity shocks. Figure 6 shows that home and foreign investors' consumption are initially equalised, but foreign consumption rises above home consumption because the home lending rate is higher during the transition to a steady state.
Figures 7 and 8 illustrate the response to a home productivity decline in the case where leverage is lower (κ = 0.5), for partial and full portfolio diversification respectively. In Figure 8, full diversification entails the home country investors holding only 25 per cent of the home equity, while in Figure 7 home country investors are constrained to hold 75 per cent of home equity. The pattern of responses is very similar to that in the high leverage case, but the magnitude of the responses is lower – borrowing and asset disinvestment are both less than in the previous case, although there is still a substantial multiplier effect of the original shock on total borrowing.
4.3 Unconditional Moments
Table 4 reports the unconditional moments of the model under the assumption that productivity shocks in both countries follow identical but uncorrelated distributions, given by Equation (25).
| Leverage constraints | None | High (LR=5) | Low (LR=2) | |||
|---|---|---|---|---|---|---|
| Diversification | Partial | Full | Partial | Full | Partial | Full |
| SDEV(CI) | 2.9 | 3.0 | 3.9 | 4.0 | 3.1 | 2.9 |
| SDEV(CS) | 0.4 | 0.5 | 0.8 | 0.9 | 0.5 | 0.5 |
| SDEV(q) | 4.7 | 5.2 | 4.7 | 4.9 | 5.1 | 5.0 |
| SDEV(R) | 0.6 | 0.7 | 2.0 | 2.0 | 0.9 | 0.9 |
SDEV(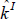 ) ) |
0.8 | 0.9 | 11.0 | 11.3 | 4.2 | 4.0 |
| CORR(q1, q2) | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 |
CORR(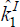 , ,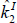 ) ) |
0.02 | 0.04 | 0.99 | 0.98 | 0.99 | 0.98 |
| CORR(R, R*) | – | – | 0.99 | 0.99 | 0.99 | 0.97 |
As is evident from the figures, the model with binding leverage constraints displays substantially more overall volatility than the model where leverage constraints are absent. Consumption of investors is 50 per cent more volatile with ‘loose’ leverage constraints, and consumption of savers is twice as volatile. Asset price volatility is relatively unchanged with and without leverage constraints but investment volatility is vastly higher, as is clear from a comparison of Figures 3 and 5. Investment correlation across countries is essentially zero in the economy without leverage constraints, but almost perfect in the economy with leverage constraints. Table 4 therefore underscores the main message of the paper. In the presence of credit market imperfections, balance sheet linkages across financial institutions can generate a very powerful mechanism for the international transmission of business cycle shocks.
4.4 Gross Portfolio Adjustment
In the first-order approximation of the model described in Figures 3–8, the
dynamics are computed around a constant portfolio position. Changes in the
portfolio affect the evolution of the real economy only at the second-order
level. Nevertheless, we may still compute the implied adjustments in the gross
portfolios using the approach of Devereux and Sutherland
(2009).[10]
In response to a negative technology shock, investors in both countries will adjust
their gross external positions. Initially, the home country investors have
a position of 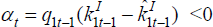 , implying that their net holdings of domestic
equity is negative, while net holdings of foreign equity are positive. In
response to a negative home productivity shock, gross asset holdings are adjusted
downward. Holding of domestic equity increases (the net position gets less
negative), and holding of foreign equity decreases. This occurs in both the
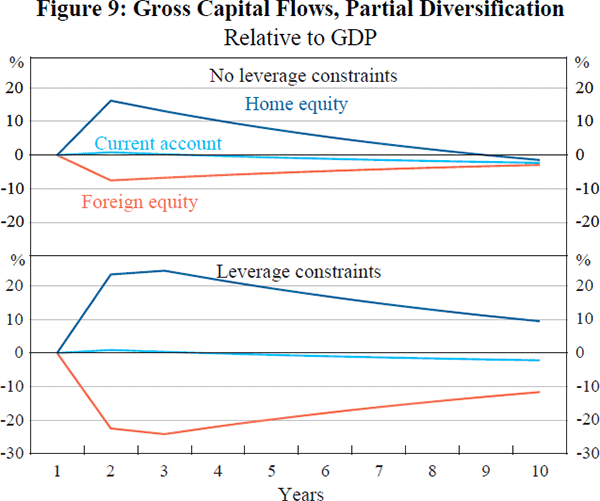
economy without leverage constraints and that with leverage constraints, as
illustrated in Figure 9. The current account locus represents the movement
of the home economy's net foreign asset position in each case, given that
the country begins holding the optimal portfolio. In each case NFA increases,
because the country is hedged against the possibility of a negative productivity
shock. But the positive movement in NFA is comprised of an increase in the
holdings of home equity, and a reduction in the holdings of foreign equity
– investors scale down their outstanding positions on each side, selling
some of their foreign equity and buying back home equity. Equivalently, home
agents reduce their outstanding holdings of foreign equity, and foreign agents
reduce their holdings of home equity. Thus there is a reduction in gross capital
flows, similar to that seen in the recent data discussed in Section 2.
As Figure 9 illustrates, this dynamic response occurs in both the unconstrained
and constrained economies. But the scale of the drawdown is much bigger in
the leverage-constrained economy. In that case, the fall in holdings of foreign
equity (and reduction in foreign holdings of home equity) is approximately
three times as large as in the unconstrained economy. Again, the presence
of balance sheet constraints imparts a substantial magnification to the response
of gross capital flows to the original shock.
, implying that their net holdings of domestic
equity is negative, while net holdings of foreign equity are positive. In
response to a negative home productivity shock, gross asset holdings are adjusted
downward. Holding of domestic equity increases (the net position gets less
negative), and holding of foreign equity decreases. This occurs in both the
economy without leverage constraints and that with leverage constraints, as
illustrated in Figure 9. The current account locus represents the movement
of the home economy's net foreign asset position in each case, given that
the country begins holding the optimal portfolio. In each case NFA increases,
because the country is hedged against the possibility of a negative productivity
shock. But the positive movement in NFA is comprised of an increase in the
holdings of home equity, and a reduction in the holdings of foreign equity
– investors scale down their outstanding positions on each side, selling
some of their foreign equity and buying back home equity. Equivalently, home
agents reduce their outstanding holdings of foreign equity, and foreign agents
reduce their holdings of home equity. Thus there is a reduction in gross capital
flows, similar to that seen in the recent data discussed in Section 2.
As Figure 9 illustrates, this dynamic response occurs in both the unconstrained
and constrained economies. But the scale of the drawdown is much bigger in
the leverage-constrained economy. In that case, the fall in holdings of foreign
equity (and reduction in foreign holdings of home equity) is approximately
three times as large as in the unconstrained economy. Again, the presence
of balance sheet constraints imparts a substantial magnification to the response
of gross capital flows to the original shock.
Footnote
This involves taking a second-order expansion of the dynamic model, in conjunction with a third-order expansion of the portfolio selection Equation (8). [10]