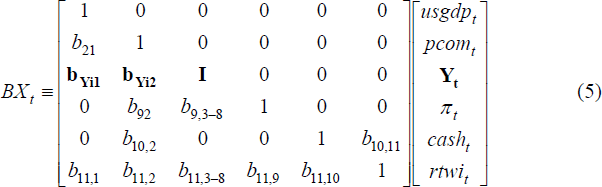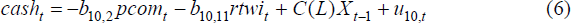RDP 2008-01: A Sectoral Model of the Australian Economy 3. A Sectoral Model of the Australian Economy
April 2008
The first model that we use to analyse the sectoral effects of monetary policy includes all of the following expenditure components of Australian GDP: dwelling investment, machinery & equipment investment, household consumption, exports, imports and a residual term that includes inventories, public demand and the remaining components of business investment.[3] In what follows, these variables are stacked so as to form a (6x1) vector Y. Although other specifications were examined, this choice of variables best satisfies the trade-off between including the largest and most cyclical components of GDP, while ensuring that the size of the SVAR remains manageable.
We include US GDP (usgdp) to capture the important influence that global economic developments can have on economic conditions in Australia. This approach is consistent with previous Australian VAR studies (Dungey and Pagan 2000; Suzuki 2004; Berkelmans 2005).[4]
Previous VAR studies have found that the inclusion of commodity prices (pcom) helps to resolve the ‘price puzzle’, in which unexpected increases in interest rates are followed initially by increases in the price level (Sims 1992). Commodity prices have added relevance for the Australian economy because commodities make up a large share of Australia's total exports.
We include the rate of underlying consumer price inflation (π) rather than the level of the consumer price index because inflation has been the explicit target of monetary policy for more than half of our sample and the underlying series is less noisy (Berkelmans 2005). In addition, the model contains no nominal activity variables, and the rate of change of prices is the logical variable to interact with the real variables and the nominal interest rate.
The inclusion of the overnight cash rate (cash) and a measure of the real exchange rate (rtwi) is standard (Brischetto and Voss 1999; Dungey and Pagan 2000; Berkelmans 2005). The overnight cash rate has been the chief instrument of monetary policy since the float of the dollar in December 1983, which spans our entire sample. The real trade-weighted exchange rate is an important macroeconomic variable in a number of respects, including through its influence on Australia's trade flows.[5]
3.1 Identification
We identify the structural shocks in our SVAR by placing restrictions on contemporaneous relationships between the variables as shown in Equation (5), which is the left-hand side of Equation (1):
Each non-zero bij coefficient in Equation (5) indicates that variable j affects variable i contemporaneously. The coefficients on the diagonal are normalised to 1, while the other entries in the matrix are constrained to be zero. (Recall that Yt is a (6x1) vector, hence the need for the (6x6) identity matrix I in the matrix B.) The system is over-identified – that is, there are more restrictions than are required to just identify the model.[6]
As the main objective of this paper is to examine the impact of monetary policy on the sectoral components of GDP, it is important that we have a well-specified monetary policy reaction function. From Equation (5), it follows that the equation for the cash rate can be written as:
Accordingly, when the RBA makes its monetary policy decisions it has current-quarter information on commodity prices and the real exchange rate, while information about the other variables is available only with a lag.[7] In this framework a monetary policy shock is simply a movement in the short-term interest rate that the model is unable to predict based on the estimated reaction of policy-makers to movements in the other variables in the system over the sample period.
The explanations for the other restrictions are as follows. The domestic variables are assumed not to affect the foreign variables, reflecting the assumption that Australia is a small open economy (this holds for all lags of the domestic variables as well). US GDP is ordered before commodity prices, which is typical in international VAR studies (Christiano, Eichenbaum and Evans 1996; Cushman and Zha 1997), but is a point of difference from Brischetto and Voss (1999) and Berkelmans (2005). This restriction follows from the observation that, over our sample, large movements in commodity prices have tended to result from fluctuations in the global demand for commodities, rather than the supply-driven price movements that characterised the 1970s.
We allow foreign shocks to affect domestic variables contemporaneously, with two exceptions. The first prevents monetary policy from reacting immediately to shocks to US GDP, reflecting informational lags. The second prevents shocks to US GDP from flowing through to domestic inflation immediately (see Berkelmans 2005).
Following Raddatz and Rigobon (2003), we assume that shocks to individual components of GDP take at least one quarter to affect the other components of GDP (as reflected in the (6x6) identity matrix, I). Placing some restrictions on the contemporaneous relationships between the GDP components is necessary to identify the SVAR. In our sensitivity analysis we consider an alternative recursive identification of the GDP components. However, a recursive identification is not our preferred method because of the difficulty in coming up with a convincing theoretical justification for any particular temporal ordering of the GDP components.
We allow inflation to respond contemporaneously to domestic output. This assumption is common in both domestic (Brischetto and Voss 1999; Dungey and Pagan 2000; Berkelmans 2005) and international (Bernanke and Blinder 1992) studies. Other domestic variables affect inflation only with a lag of one quarter (see Section 5 for further discussion of this point). Finally, the real exchange rate is assumed to respond contemporaneously to all other variables, as is common in VAR studies.
3.2 Estimation
The model is estimated using quarterly data from December 1983 to September 2007, yielding 96 observations. By restricting the sample to the post-float period, our results should be less vulnerable to parameter instability. However, even over this relatively short period there have been significant changes in the conduct of monetary policy (such as the move to inflation targeting in 1993) and other structural changes to the economy. We deal with this in our sensitivity analysis by comparing the results from our baseline model to those from models estimated over two shorter sub-samples. In all cases the impulse responses should be interpreted as representing sample averages rather than how the economy would respond to shocks today.
In our baseline specification, all variables enter the model in log-levels, with the exception of the inflation rate and the cash rate, which enter in percentage point terms. Although unit root tests suggest that many of the variables in the SVAR are likely to be non-stationary, estimation in levels is still consistent and avoids losing information about possible long-run relationships between the variables in our model (Sims 1980; Sims, Stock and Watson 1990).[8] It is also the approach most commonly taken in the SVAR literature.[9]
Correct specification of the model also requires the inclusion of the appropriate number of lags. If too few lags are included, the residuals may not be white noise and hence standard inference is inappropriate. On the other hand, including too many lags risks over-parameterising the model (Hamilton 1994). Our specification tests (Akaike Information Criterion (AIC) and the Schwartz Bayesian Information Criterion (BIC)) suggest that either three, four or five lags are optimal. While we use three to reduce the number of parameters to be estimated, the results are largely insensitive to this choice.
We estimate standard errors using the bias-correcting bootstrap method outlined in Kilian (1998). This method involves a preliminary bootstrap to correct possible bias in the coefficient estimates of the reduced-form VAR. A subsequent bootstrap is used to calculate the empirical distribution of impulse responses.[10]
Footnotes
We include aggregate consumption in our baseline specification rather than splitting consumption into its durable and non-durable components because we need to limit the size of the SVAR. In an alternative specification (available on request) we found that durable goods consumption was more interest sensitive than non-durable goods, but less interest sensitive than dwelling investment and machinery & equipment investment. [3]
Because this relationship appears to have become weaker in recent years, we include a broader measure of global economic activity – a weighted average of the GDP of Australia's major trading partners – in our sensitivity analysis in Section 5. [4]
More information about the variables used in this paper is provided in Appendix A. [5]
As is common in the VAR literature, the likelihood ratio test for the validity of our identifying restrictions suggests that they should be rejected. [6]
This echoes previous bank research by Brischetto and Voss (1999) and Berkelmans (2005). [7]
Results of the unit root tests are available from the authors. [8]
As a robustness check, we estimated our model with all variables other than the cash rate expressed as quarterly percentage changes. This transformation did not alter the relative responsiveness of the components of domestic GDP to a monetary policy shock. However, the response of inflation to a monetary policy shock is strongly positive for several quarters, reinforcing our preference for our baseline model. The inclusion of a linear time trend and dummy variables for the period around the introduction of the Goods and Services Tax in 2000 also had little effect on our core results. [9]
We use 500 replications in the first bootstrap and 1,000 replications in the second. [10]