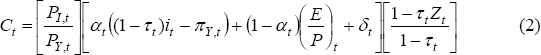RDP 2007-09: Private Business Investment in Australia 3. Modelling Aggregate Investment

3.1 The Neoclassical Model

The starting point for the empirical analysis that follows is the traditional Jorgenson (1963) neoclassical model. In this model a representative firm chooses capital and other inputs to maximise profits subject to the capital accumulation identity, K_t = (1 – δ_t)K_t−1 + I_t, where K_t and I_t denote the capital stock and investment respectively. The first-order condition from this problem (using a constant elasticity of substitution (CES) production function) implies that the optimal capital stock, K^* , is as follows:

where: C is the cost of capital; and δ is the elasticity of substitution between factors of production (for the Cobb-Douglas production function, δ = 1). If there are no frictions (real or financial) impeding adjustment, then the capital-to-output ratio should have an inverse relationship with the cost of capital. Even in the presence of frictions that delay adjustment of the actual stock to the optimal level given by Equation (1), the same inverse relationship should exist over the long run.

The cost of capital is measured according to the standard Jorgenson (1963) and Hall and Jorgenson (1967) formula, with the debt-equity split and present value of depreciation calculation (using the exponential method) similar to the approach in La Cava (2005). That is,

where: capital costs increase with the purchase price investment goods (relative to GDP prices) (P_I,t/P_Y,t); the cost of funds to the firm; the physical rate of depreciation (δ_t) and the taxation of corporate profits (τ_t is the corporate tax rate). The latter is offset to some extent by the tax deductibility of the present value of depreciation expenses (Z_t). The cost of funds to the firm is measured as a weighted average of the real after-tax business interest rate ((1 − τ_t)i_t − π_Y,t) – which depends on the nominal interest rate on debt, i_t, and expected inflation (assumed to be actual inflation π_Y,t) – and the cost of equity, as measured by the earnings-price ratio (E/P)_t.^[6] α_t is the share of debt financing used relative to the total of debt and equity. Naturally, there are many ways to measure these variables, and different assumptions can lead to a wide dispersion of possible measures, some of which are discussed further below. See Dews, Hawkins and Horton (1992) for an earlier discussion of issues related to the cost of capital with particular reference to Australia.

3.2 The Q Model

An alternative approach traditionally used in the investment literature is the Q model, attributable to Tobin (1969). It has since been recognised to be a variant of the neoclassical model in which costs of adjusting the capital stock are explicitly incorporated in the firm's maximisation problem (Hayashi 1982). In its modern form, the Q theory suggests a positive relationship between the investment rate and marginal Q, defined as the value of an additional unit of capital relative to its replacement cost. Q operates as a summary variable that incorporates expectations about the future returns on a firm's capital. When Q is high, firms have an incentive to invest as the expected return on capital is greater than its cost, whereas a low Q will discourage investment. In practice, marginal Q is not observable and therefore average Q – measured as the value of existing capital to its replacement cost – is typically used in its place.

3.3 Empirical Literature

There were concerted efforts to apply the neoclassical and Q models to Australian data throughout the 1970s, 1980s and early 1990s, though with mixed results.^[7] A common feature of the models estimated from the early 1990s onwards was the inclusion of cash-flow variables (usually profits) (aggregate studies include Debelle and Preston 1995, (firm-level) panel data studies include Mills, Morling and Tease 1994 and La Cava 2005). Work over the past decade has been relatively scarce, particularly with regards to aggregate investment. The more recent work includes Bond and Hernandez (2003), who estimate an error-correction model based on the neoclassical framework, Swift (2006), who investigates the role of the exchange rate on manufacturing investment but does not incorporate more traditional variables, and Andersen and Subbaraman (1996), who estimate a traditional Q model.

The common theme across the literature is that output is generally an important driver of Australian investment. Cash-flow variables, where included, have also been found to be important; these are included to account for financial frictions that may inhibit the firm's ability to adjust its capital stock optimally. While significant effects have been found for price variables – mainly the real user cost of capital or Q – the size of these effects is generally small and the results are not overly robust, and they depend on issues related to the measurement of these variables. The findings of the Australian literature are overall similar to the findings from Chirinko's (1993) survey of the US literature that quantity variables are generally more important than price variables for understanding investment.

The traditional neoclassical and Q models remain the basis of most empirical papers. Their use is justified by Oliner et al (1995) who show that these traditional models outperform some more modern alternatives, in particular, Euler equation models. Even so, Chirinko's (1993) survey of the US literature concludes that ‘the Q model's empirical performance has been generally unsatisfactory’ (p 1891), while for Australia, Debelle and Preston (1995) suggest that ‘Q-related variables do not appear to be good explanators of investment’ (p 23). Other papers argue the importance of correctly measuring Q (which might be distorted by speculative movements in share prices, for example) in order to estimate its relevance for investment, although obtaining ‘correct’ measures is not easy.^[8] Hence, the models in this paper are based on the traditional neoclassical model.

3.4 Computing Equipment

Recent empirical literature highlights problems that can arise when modelling investment when it includes computing equipment. In addition to the problems created by computing equipment investment already mentioned in Section 2, Bakhshi, Oulton and Thompson (2003) show that the neoclassical equilibrium relationship, described by Equation (1), is misspecified when capital is made up of two types of goods whose prices have shifted relative to each other. Earlier work by Tevlin and Whelan (2003) also highlighted misspecification in the estimated model, but from the perspective that it was no longer correct to assume that the depreciation rate for total equipment investment is constant, as is typically the case.^[9] See Appendix B for further discussion.

Footnotes

The value of a firm (P) is equal to the sum of its future earnings (E), discounted by the cost of its equity capital (k_e); that is, 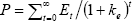. Assuming a constant growth rate of earnings (γ) and rearranging implies k_e = (1 + g)E₀/P₀ + γ. If γ is constant, k_e will move in line with E/P. According to Miller and Modigliani (1961), the value of the firm does not depend on whether the firm pays out earnings as dividends, or reinvests them at k_e. [6]

See Hawkins (1979) for a review of the early Australian literature. The RBA and Commonwealth Treasury worked in this area in the context of their in-house macroeconometric models (see, for example, Edey, Kerrison and Menzies 1987 and Simes 1987). [7]

Andersen and Subbaraman (1996) have more success using Q models for Australia by separating fundamental movements in the value of firms from speculative movements. [8]

While the assumption of a constant depreciation rate is made explicitly in the traditional formulation of models for the investment-to-capital ratios, it is also important in the approximation made in Equation (3). [9]