RDP 2006-10: The Performance of Trimmed Mean Measures of Underlying Inflation 7. Conclusion
December 2006
- Download the Paper 329KB
This paper has examined the relative performance of the headline CPI, exclusion-based cores, and trimmed means as measures of underlying inflation. Although there are many other candidates for measures of underlying inflation, the measures studied here share the benefit of being easily calculated and communicated and not subject to revision. Based on data for four economies, we find that trimmed means tend to outperform headline and exclusion-based core measures on a range of different criteria, which indicate that trimmed mean measures can be thought of as having a higher signal-to-noise ratio than either of the other measures. This makes trimmed means more useful for extracting information about the current trend in underlying inflation from the relatively noisy monthly or quarterly prices data.
The results lend support to the use of trimmed means as useful measures of underlying inflation at the current juncture where the growth of China and other emerging markets is having two offsetting effects on global inflation. Whereas some central banks have tended to focus on headline inflation and others have focused more on exclusion measures, our results provide some justification for a middle path, namely using trimmed mean measures which deal with outliers at both ends of the distribution of price changes in a symmetric manner.
Our results suggest a few important technical points regarding the calculation of trimmed means. First, the performance of trimmed means (especially large trims such as the weighted median) can be improved by breaking up expenditure items which have a large weight in the CPI. We show that breaking up the large implicit rent component in the US CPI into four regional indices sometimes has a substantial effect on estimates of weighted median inflation. Second, when calculating trimmed means based on the distribution of annual price changes it is preferable to avoid using the weighted median but rather to use significantly smaller trims. These two points can be viewed as evidence that using a finer degree of disaggregation – either across time or across items – will often improve the performance of trimmed mean measures. Third, when using measures based on cumulated monthly or quarterly trimmed means, there is a fairly wide range of trims that appear to perform well. This is illustrated in Figure 11 which combines the results from several of the tests above. In particular, we take the results from Figures 4, 7 and 8 and construct a simple summary measure of how close each trim is to an overall optimal one.[31] The optimised trims (according to this measure) are around 20 per cent for the United States and Australia and around 35–40 per cent for Japan and the euro area. However, if we define trims that capture 80 per cent of the feasible gains as being close to optimal, the range of ‘close to optimal’ trims starts at between the 5 and 10 per cent trims and extends all the way to the 50 per cent trim (weighted median) for all countries. In none of these four economies would the exclusion measure have been included among the ‘close to optimal’ measures of underlying inflation (although the US core measure would come close). The key point in our view is that there seems to be a wide range of trims that offer substantial improvements over the headline or exclusion measures.
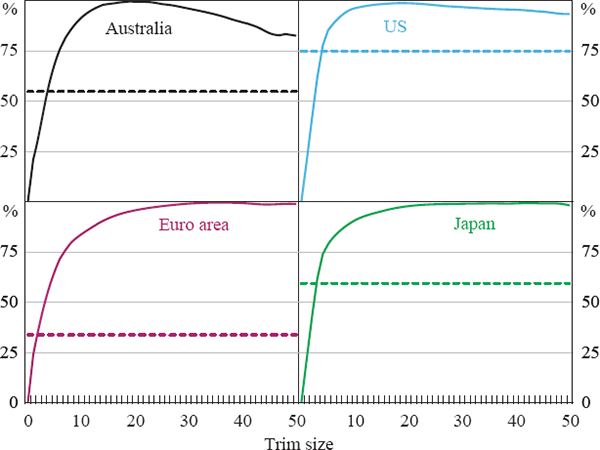
Note: Dashed lines represent exclusion measure results.
Although our results suggest that trimmed mean measures are useful indicators of underlying inflation pressures, we cannot rule out the possibility that further research will suggest additional improvements to the calculation of these measures. In addition, there will inevitably be trade-offs between various goals for underlying measures. For example, if the goal is to arrive at a series which is very smooth and gives good signals of changes in the trend level of underlying inflation then trimming a significant proportion of the distribution of monthly or quarterly price changes may be optimal. Yet the more that is trimmed, the greater the likelihood that the remaining part of the distribution may no longer give a good reading of the level of overall inflation: that is, a small amount of bias may be introduced. The latter point would suggest that if there is a choice between a range of trims that appear – as in Figure 11 – to be close to optimal, it may be best to err towards the lower end of the range to minimise the possibility of bias.
All in all, it is unlikely that any single measure of underlying inflation can be held up as the ‘best’ measure at all times and in all countries. The relative usefulness of different measures may change depending on the nature of the shocks, suggesting that central banks and other analysts should look at a range of measures of inflation in assessing inflation developments. Trimmed mean measures, calculated to reflect the characteristics of the distribution of price changes within each country, should have a reasonably prominent place in any suite of measures, although there will be no substitute for detailed analysis of all the factors driving the CPI at any point in time.
Footnote
Specifically, for the data in each of the three figures we calculate the maximal feasible improvement according to that criterion (in the case of Figure 8 we use the CPI prediction results), and the proportion of feasible improvement that is captured by each trim and by the exclusion measure. We show the mean of these three measures as a summary measure of how close each underlying measure is to being optimal. [31]