RDP 2006-10: The Performance of Trimmed Mean Measures of Underlying Inflation 3. Background on Trimmed Mean Measures of Underlying Inflation
December 2006
- Download the Paper 329KB
3.1 Definition of Trimmed Mean Measures
As discussed above, policy-makers and other analysts often make use of measures of core or underlying inflation, which should be subject to less noise than headline inflation and should provide a better measure of the trend in inflation. One simple method of removing noise is to use an average of recent monthly or quarterly rates, for example using annual rates of inflation rather than just the price movement in the latest month or quarter. Indeed, Cogley (2002) proposes an exponentially weighted average of past rates as a measure of underlying inflation. While this will be effective in creating a smoother measure, it will be a backward-looking one and will probably place insufficient weight on the information in the data for the most recent month or quarter.[9] In addition, as was seen in a number of countries in late 2006, annual rates of inflation can change rapidly, not only because of some movement in prices in the latest period, but because of movements in prices that happened a year earlier.
Accordingly, measures of underlying inflation typically do not use time averaging but instead look to down-weight or exclude the impact of particular items in each period. One common approach is to calculate the inflation rate for the CPI basket excluding a few items which historically have had particularly volatile prices. One frequently used measure of underlying inflation (sometimes referred to as ‘core inflation’) is the overall CPI excluding food and/or energy (and possibly other volatile items). These ‘exclusion’ measures of underlying inflation remove the direct effect of movements in the prices of those items on the rationale that they tend to be volatile and often not reflective of the underlying or persistent inflation pressures in the economy. However, exclusion measures of underlying inflation may not always be appropriate. For example, there may be large temporary movements in other components of the CPI that are not excluded from such measures of core inflation. In addition, there may indeed be information about underlying inflation pressures in the food and energy components, but such information will be lost in an exclusion measure.
Trimmed mean measures, first proposed by Bryan and Pike (1991) and Bryan and Cecchetti (1994), represent an alternative approach to measuring underlying inflation. Whereas exclusion measures remove some pre-specified items in every period regardless of whether or not their price changes are extreme, trimmed mean measures exclude – or more correctly down-weight[10] – the impact of items based on whether or not their price changes appear to be outliers in the period in question. These measures represent an attempt to estimate the central part of the distribution of price changes, and provide a measure of inflation that is not excessively affected by large price changes – either increases or decreases – in individual items.
Formally, the trimmed mean rate of inflation is defined as the average rate of inflation after trimming away a certain percentage of the distribution of price changes at both ends of that distribution. In all the work that follows, we focus on symmetric trimmed means. The first step in calculation is to order the distribution of price changes for any period from lowest to highest. The n per cent trimmed mean rate of inflation for that period is calculated by excluding n per cent (taking into account the weights of the components in the CPI) from the top and bottom of the ordered distribution of price changes and then taking the weighted average of prices in the remaining central (100-2n) per cent of the distribution. A whole suite of such measures can be provided by trimming an increasing proportion of the distribution from either end. At one extreme, the 0 per cent trimmed mean corresponds to the conventional headline rate of inflation. At the other extreme is the weighted median or the 50 per cent trimmed mean which is the price change at the 50th percentile (by weight) of the ordered distribution of price changes.
The statistical rationale for trimmed mean measures is usually based on the evidence that distributions of price changes for individual CPI components tend to show excess kurtosis, or fat tails. Fat-tailed distributions are more likely to yield extreme observations from one of the tails of the distribution, and it is possible that these observations are not balanced in a given period by an offsetting movement in the price of another CPI component. Under such circumstances, trimmed means are likely to be better estimators of the central part of the distribution than are sample means. Roger (2000) provides a further discussion of the case for using trimmed means rather than simple means.[11]
3.2 Technical Issues in Calculating Trimmed Mean Measures
There are a number of technical, but nonetheless important, issues that present themselves in the calculation of trimmed mean measures of underlying inflation. These relate to particular characteristics of the actual distribution of price changes. In general, they are concerned with improving the performance of trimmed mean measures by making the underlying distribution of price changes smoother and more continuous, and correcting for possible average bias (relative to CPI inflation).
3.2.1 Symmetric or asymmetric trims
In this paper we limit our analysis to symmetric trimmed means, which remove the same proportion of the distribution at the high and low ends. However, some other applications have suggested the use of asymmetric trims. For example, Roger (1997) suggested the use of the 57th percentile for the New Zealand CPI, while Dolmas (2005) suggests trimming 25 per cent off the top and 19 per cent off the bottom of the distribution for the US personal consumption expenditures (PCE) chain price index.
Our use of symmetric trims in this paper is based both on a priori preferences and concerns about the communication issues surrounding underlying measures. In particular, intuitively it seems more desirable that outliers at both ends should be treated similarly. Perhaps more importantly, it may be easier to explain symmetric trims to the public, without raising concerns that the central bank is trying to manipulate measures of the inflation rate.
The rationale for asymmetric trimming has typically been based on the finding that distributions of price changes are skewed so that a symmetric trimmed mean may be biased with respect to CPI (mean) inflation. However, the potential for bias in trimmed means will depend not just on the shape of the distribution, but also on the relationship between the relative volatility of prices and their average rate of growth. For example, if prices for services tend to be less volatile but to rise faster than those for goods then they will tend to be trimmed less often, which would result in a tendency for trimmed means to be biased upwards.
In the end, the decision as to whether asymmetric trimming should be employed requires a judgment that any apparent bias in some historical period is systematic and likely to persist into subsequent periods. Our own analysis in Section 5.2 finds little evidence of bias for the four economies we study, suggesting that asymmetric trims may typically not be necessary. In addition, it is worth noting that the performance of trimmed mean measures against the other criteria in Section 5 would be penalised to the extent that the measures were biased, so the strong performance of these measures suggests that bias is not a major issue.
3.2.2 Choice of frequency of price changes
Annual trimmed mean measures of inflation are often calculated by using the distribution of monthly or quarterly price changes to calculate measures of monthly or quarterly underlying inflation, which are then cumulated to get an underlying price index which can be used to generate the annual rate of underlying inflation. However, an alternative is to calculate the annual rate of underlying inflation by taking the distribution of year-ended price changes for all the CPI sub-components and calculating a trimmed mean of these annual rates.[12]
In general, it might be expected that these should yield very similar estimates of annual underlying rates. However, consider the extreme case where the CPI could be calculated on a daily basis. In this case, we would expect that most individual prices in the economy would remain unchanged, so the median price change across expenditure classes would be zero, and cumulating these daily rates over a full year would suggest a zero annual rate of underlying inflation. By contrast, a weighted median measure based on the distribution of annual changes would indicate a very different rate, no doubt much closer to the (unobservable) true underlying rate. Of course, this example is extreme because CPIs are not calculated on a daily basis. So any bias from using monthly or quarterly price changes is likely to be much smaller. Nevertheless, given that there will typically be some items with prices changed (or sampled) irregularly, there may be a case for using price change distributions over longer horizons, and the two methodologies may sometimes give different pictures of underlying inflation pressures.[13] We provide some evidence on this issue in Section 5.1.
3.2.3 Seasonality
One related issue is the case of irregular price changes due to seasonal price adjustment, including for some administered prices. In such cases, a typical pattern will be for a price to be unchanged for most of the year, then to jump in one particular month or quarter by a relatively large amount. Many countries do not seasonally adjust the raw price data in their CPIs. In such cases the infrequent price adjustment may have a noticeable effect on the headline CPI, and a more significant effect on the calculation of trimmed mean measures. In particular, for a range of trims we would expect these items to be trimmed in the period when their prices are increased but not trimmed in the periods when their prices are unchanged. If there are a sufficient number of items with such characteristics, trimmed mean estimators based on non-seasonally adjusted data can be downwardly biased, as has been shown by Roberts (2005) using Australian data. However, a simple response which should eliminate this potential downward bias is to use seasonally adjusted prices for individual expenditure items which appear to have seasonal prices. This is the approach we follow below.
3.2.4 Treatment of housing or other large expenditure items
Another important issue in calculating trimmed mean measures for some countries is that such measures, in particular the weighted median, can be significantly affected by the presence of items that have a large weight in the CPI basket. This is most relevant in the case of housing costs. In the United States the component for ‘owners' equivalent rent of primary residence’ accounts for around 23 per cent of the total CPI, compared with an average weight of 1.1 per cent for the 69 other expenditure items in our dataset. One consequence is that this one item is the median item fully 59 per cent of the time in our sample from 1993 to 2006. This component is also relatively large in Japan, at about 14 per cent of the CPI. In the other economies we examine, the largest items in the CPI are significantly smaller, accounting for less than 8 per cent of the total CPI in Australia and the euro area.[14]
We can use US CPI data to illustrate the consequences for trimmed means of having an item with a very large expenditure weight. The top panel of Figure 1 shows the distribution of annualised monthly price changes for a particular month, June 2002, along with the weighted median for that month. In the bottom panel, we show the distribution of price changes when more disaggregated data for implicit home-owners' rent are used. This component cannot be disaggregated further into finer expenditure items, so instead we calculate trimmed means after breaking it into regional subcomponents.[15] Regional price changes for this item are published by the Bureau of Labor Statistics (BLS), and we estimate appropriate weights by using dwelling stock data from the US Census Bureau. This gives weights in the total CPI of around 4 per cent for implicit rent in the north-east, 9 per cent for the south, 5 per cent for the mid-west and 5 per cent for the west. The adjustment results in a distribution that is somewhat smoother and much less peaked.
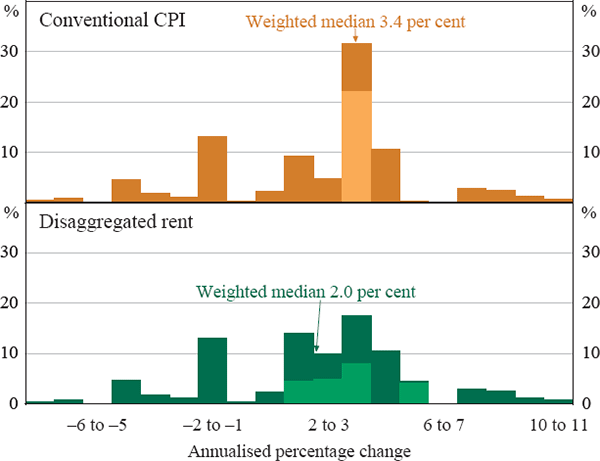
Notes: Bars do not sum to 100 because small proportion of distribution at both extremes is not shown. Lighter shading shows implicit rent components.
The conventionally calculated rate of mean CPI inflation is obviously unaffected by this change. However, the significant shift in the shape of the distribution results in a large shift in the weighted median inflation rate, from an annualised rate of 3.4 per cent using the aggregated data to 2.0 per cent using the less aggregated data. In contrast, the effect on smaller trims, such as the 25 per cent trim, is much smaller.
As is shown in Figure 2, this issue is particularly important during 2001 and 2002, when our adjustment reduces the cumulated annual inflation rate for the weighted median by as much as 0.7 percentage points, moving it closer to other measures of inflation at that time. Furthermore, the analysis in Section 5 suggests that the disaggregation of the rent component results in an improvement in the statistical performance of trimmed mean measures. This accords with the notion that these measures are likely to yield more accurate indications of the central tendency of the distribution when reasonably disaggregated price data are available and the distribution of the underlying changes is smoother.[16],[17] Unfortunately, data constraints prevent us conducting a similar disaggregation for Japan.
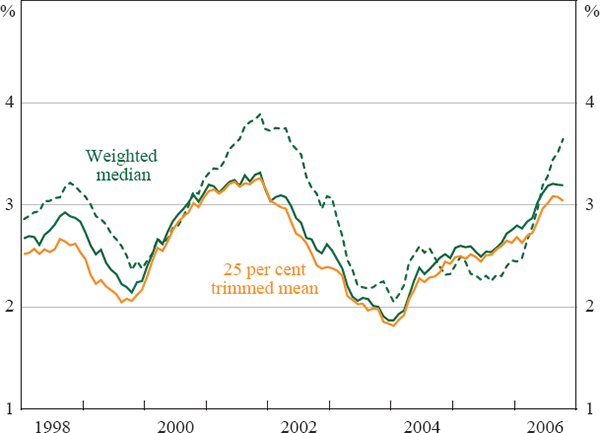
Note: Dashed line is calculated without disaggregating the implicit rent component.
Footnotes
However, a concurrent paper by Gillitzer and Simon (forthcoming) represents a promising advance in this area, proposing a varying degree of time averaging for different items in the CPI basket, with only minimal averaging for items with prices that are relatively smooth and a higher degree of averaging for items with more volatile prices. [9]
We say ‘down-weight’, because even when an expenditure item is trimmed and ‘excluded’ it still affects the trimmed mean. In particular, the fact that an item has been trimmed in any period means that some other item which experienced a relatively high or low price change will not be trimmed. Trimmed mean measures are accordingly sometimes referred to as limited influence measures. [10]
More complex versions of trimmed means are also feasible (see Roger 2000 and Aucremanne 2000), but we limit our analysis to the more standard applications. [11]
For example, the measures calculated by the RBA and the Federal Reserve Banks of Cleveland and Dallas are calculated at the quarterly or monthly level and then cumulated to get annual rates. In contrast, the Bank of Canada and Reserve Bank of New Zealand calculate trimmed means from the distribution of year-ended price changes. However, there are some drawbacks to the latter method. The measure of annual underlying inflation cannot be simply transformed to yield a corresponding continuous price index, nor used to produce consistent estimates of higher frequency underlying inflation. In addition, it presents challenges at times of CPI reweightings (especially involving introduction or removal of expenditure items). [12]
An alternative solution to this problem will be seasonal adjustment, as is discussed in the next section; asymmetric trims would be another option, subject to the caveats discussed above. [13]
This reflects different methodological approaches to the treatment of housing costs. For example, Australia uses the ‘net acquisitions approach’ by including only the construction cost (but not land component) of additions to the owner-occupier dwelling stock, while the United States and Japan follow the ‘consumption approach’ by including an implicit cost (the estimated rental value) of housing for all owner occupiers. All three (and the euro area) include an item capturing the cost of renting for that part of the population that rents. [14]
It might be argued that consistency requires that all components should be broken up by region, but our exercise is purely intended to resolve the problems arising from components with very large weights. We leave open the question of whether it might be preferable to calculate trimmed means from distributions broken up by component and geographic region. [15]
One consequence of breaking up implicit home-owners' rent into four components is that one of these is the median item ‘only’ 38 per cent of the time, versus 59 per cent when it is a single item. [16]
See also Bryan, Cecchetti and Wiggins (1997) for additional evidence that the gains from trimmed mean measures increase as more disaggregated data are used. [17]