RDP 2006-03: Australian House Prices: A Comparison of Hedonic and Repeat-sales Measures Appendix C: Repeat-sales Alternatives

Consistent with Shiller (1991), the value-weighted arithmetic repeat-sales index can be inferred from the following regression:

where X is a (i x t) matrix of independent variables where each element i,t is equal to: the resale price if house i was resold in period t; the previous sale price if house i was previously sold in period t; and 0 otherwise.^[23] The vector Y of dependent observations is defined such that Y_i equals the initial sale price of house i if sold in the base period, and 0 otherwise. The reciprocal of the element t of β provides an estimate of the mean price in period t relative to the mean price in the base period.

However, as pointed out by Shiller (1991), with stochastic independent variables there exists an errors-in-variables problem. To correct for this, I take the instrumental-variables estimator proposed by Shiller, 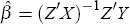, where the element i,t of Z is 1 if house i was resold in period t, −1 if house i was previously sold in period t, and 0 otherwise.

For the equally-weighted arithmetic repeat-sales index, row i of the instrumental variables regression of Equation (C1) is divided by the initial sale price of house i (for all i). The resulting index will be an equally-weighted arithmetic index. The advantage of this approach is that efficiency may be improved in estimation – a proportional error is obtained rather than a levels error – and an equally-weighted index may be conceptually preferred to a value-weighted index.

Footnote

To avoid perfect multicollinearity, the first column of X relates to the first period of sales after the base period. [23]