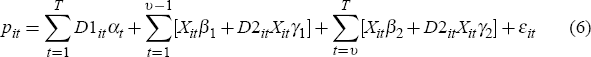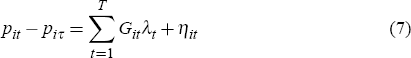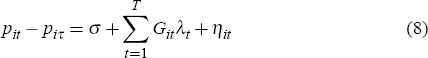RDP 2006-03: Australian House Prices: A Comparison of Hedonic and Repeat-sales Measures 4. An Empirical Comparison of Alternative Measures
May 2006
- Download the Paper 177KB
As previously discussed, there is no consensus regarding the preferred approach to measuring house prices, either theoretically or empirically. However, there is reason to believe that constructing more advanced measures of house prices, such as regression-based measures, may provide a better guide to pure price changes in housing than a simple median. To this end, I consider several hedonic and repeat-sales alternatives to find a preferred measure for each approach. I then compare the preferred hedonic and repeat-sales measures with each other, as well as two simple measures (a median and a mix-adjusted measure) to gauge the performance of the regression-based measures and the extent to which compositional and quality change matter.
4.1 Data
The data are based on a census of house sales (excluding apartments) in Australia's three largest cities – Sydney, Melbourne and Brisbane – which make up just over half of all house sales in Australia. These data originate from land titles offices and have been collated, matched and supplied by APM. I also use data from the REIV for Melbourne, since these data have address level information, which APM cannot provide for this city, and can be used to construct a repeat-sales measure.[9] The data are comparable to those used by the ABS in compiling their quarterly measures of house prices for Sydney, Melbourne and Brisbane. For an overview of the procedures used to clean the data prior to constructing the alternative house price measures, see Appendix B.
The data contain unit record information on each house sale, including information on: location (street address, postcode, suburb, statistical local area, statistical sub-division, statistical division and state); property type (house, cottage, villa, semi-detached, townhouse or terrace); contract and settlement dates; and the sale method (auction or private treaty). In total, I use approximately 642,000 observations for Sydney, 630,000 observations for Melbourne (350,000 observations where REIV data are used) and 436,000 observations for Brisbane.[10] In addition, a subset of the records in each sample have information on: zoning (residential, business, mixed etc); land size (measured in square metres); and the number of bedrooms and bathrooms. Finally, data are quarterly from March 1993 to September 2005, and are recorded according to contract dates.
4.2 Hedonic Measures
Since economic theory does not point to a unique and superior hedonic specification, several alternatives are considered. I begin with the following specification:
The only difference between the original formulation of Equation (1) and Equation (6) is that the latter restricts βt and γt to be constant within each of two sub-samples of the data – March 1993 to December 1998 and March 1999 to September 2005. This restriction is undertaken for computational simplicity (the full unrestricted model would require a regression of approximately 12,500 variables on 642,000 observations in the case of Sydney). For the initial regressions, the characteristic variables included in Equation (6) are postcode, property type, and sale method, which maximises the sample size.[11] While postcode and sale method are not ‘true’ hedonic variables since they do not measure actual house characteristics, the postcode can be thought of as a proxy for a range of characteristics associated with the houses' location, such as the average amenities of the neighbourhood (distance from schools, the beach, the city, services and so forth), its general desirability, and the average quality of housing in the area. Similarly, the sale method might be correlated with the quality of the property being sold as higher quality housing is more likely to be auctioned.
Table 1 reports the results of these statistical tests. They generally reject the hypothesis that the implicit price relativities (implicit prices) – that is, the elasticity/semi-elasticity of price with respect to a given house characteristic – for single and repeat sales are the same.[12] Further, they reject the hypothesis that the implicit prices of characteristics do not vary through time (at least for the two sub-samples of the data, and conditional on the assumption that the implicit prices of single and repeat sales are not statistically different). This suggests that the more general specification should be used, at least for measuring the implicit prices of house characteristics. However, whether this affects the temporal component of prices, the pure price changes, is an empirical question.
| Single vs repeat sales(a) | Constant implicit prices(b) | |
|---|---|---|
| γt = 0 | βt = β\γt = 0 | |
| Sydney | ||
| Unrestricted RSS(c) | 56,828 | 57,286 |
| Restricted RSS(c) | 57,286 | 57,690 |
| F-statistic | 11.6 | 22.1 |
| (p-value) | 0.00 | 0.00 |
| Restrictions | 493 | 249 |
| Observations | 641,668 | 641,668 |
| Melbourne(d) | ||
| Unrestricted RSS(c) | 37,287 | 36,788 |
| Restricted RSS(c) | 36,788 | 36,577 |
| F-statistic | 8.2 | 214.9 |
| (p-value) | 0.00 | 0.00 |
| Restrictions | 493 | 264 |
| Observations | 348,689 | 348,689 |
| Brisbane | ||
| Unrestricted RSS(c) | 52,092 | 52,421 |
| Restricted RSS(c) | 52,421 | 53,811 |
| F-statistic | 10.5 | 105.9 |
| (p-value) | 0.00 | 0.00 |
| Restrictions | 251 | 131 |
| Observations | 436,009 | 436,009 |
|
Notes: These restrictions are tested using F-tests that adjust for
heteroskedastic-consistent standard errors. Sources: APM; REIV; author's calculations |
||
To test whether the temporal component of prices (αt) are statistically different I estimate the general hedonic model in Equation (6) jointly with a restricted equation where γt = 0, using a Seemingly Unrelated Regression (SUR). The null hypothesis that each of the αt are jointly equal for both equations cannot be rejected at conventional levels of significance. Similarly, if the SUR is re-estimated with the restricted equation γt = 0, and an equation where γt = 0 and βt is constant over time, again I find that there are no statistical differences between the pure price changes inferred.[13]
Although the data reject the various restrictions commonly imposed on hedonic regressions in the literature (that is, βt = β and γt = γ), it is still worth examining the restricted regression results. The key results for Sydney, Melbourne and Brisbane are shown in Table 2. For each city, I use a subset of the data for which the complete set of information on all characteristics are available and estimate alternative specifications that include data on postcode, property type, log land size, sale method, bedrooms, bathrooms and zoning. Two broad results are noteworthy. First, the models fit the data reasonably, with the fully specified versions explaining between 62 and 78 per cent of the variation in log prices for the three cities. Second, nearly all of the implicit price coefficients have the expected sign and are statistically significant.
| Sydney | Melbourne | Brisbane | |
|---|---|---|---|
| Constant | 10.62 | 10.71 | 8.97 |
| Land size | 0.28 | 0.19 | 0.39 |
| Property | |||
| Cottage | −0.07 | 0.08 | −0.05 |
| Semi-detached | −0.12 | −0.23 | −0.25 |
| Terrace | −0.05 | −0.02 | |
| Townhouse | −0.44 | 0.09 | −0.12 |
| Villa | −0.26 | 0.11 | |
| Sale | |||
| Pre-auction | 0.04 | 0.02 | 0.04 |
| Auction | 0.06 | 0.05 | 0.01 |
| Post-auction | 0.07 | 0.03 | 0.02 |
| Bedrooms | 0.07 | 0.16 | 0.16 |
| Bathrooms | 0.14 | ||
| Postcodes | Yes | Yes | Yes |
| Zoning | Yes | No | Yes |
| Prices growth | 8.79 | 9.69 | 10.00 |
| Adjusted R2(a) | 0.78 | 0.78 | 0.62 |
| RMSE | 0.27 | 0.25 | 0.28 |
|
Notes: Based on a common sub-sample of 25,122 observations for Sydney (4 per cent
of the total Sydney sample), 18,229 observations for Melbourne (3 per cent of
the total Melbourne sample) and 4,683 observations for Brisbane (1 per cent of the total Brisbane sample);
insignificant coefficients are italicised at the 5 per cent level of
significance. Sources: APM; author's calculations |
|||
The most important characteristic in explaining log prices in these regressions is postcode. Including the postcode in which a house is sold (a proxy for location and the amenities associated with the location) explains around 39 per cent of the log price variation in Sydney, 59 per cent in Melbourne, and 27 per cent in Brisbane when included in addition to the time dummy variables (the time dummies alone explain around 26 per cent of the variation in Sydney, 11 per cent in Melbourne and 8 per cent in Brisbane). Other characteristic variables such as log land size, property type, bedrooms, bathrooms, zoning and the sale method provide less explanatory power in total for Sydney (around 13 per cent) and Melbourne (around 8 per cent), and about the same explanatory power as the postcode for Brisbane (27 per cent). Coefficient estimates are robust to including each of the characteristic variables by themselves in the restricted hedonic regressions (results are available on request).
The results in Table 2 also appear to provide plausible estimates of the value of a range of housing characteristics.[14] Holding other things equal, a 1 per cent increase in land size corresponds to a 0.28 per cent price increase in Sydney, a 0.19 per cent increase in Melbourne and a 0.39 per cent increase in Brisbane.[15] The size and amenities of the house, as measured through the number of bedrooms and bathrooms, also has a positive effect on price. In Sydney, an additional bedroom corresponds to a 7 per cent increase in price, while an additional bathroom results in a 14 per cent increase. It should be noted, however, that the bedroom and bathroom variables are quite collinear (a correlation of 0.87 for Sydney) and that part of the strength in the magnitude of the bathroom coefficient may reflect an unobserved correlation between the number of bathrooms and other measures of the size of the house. For both Melbourne and Brisbane, an additional bedroom leads to a 16 per cent higher price (bathroom data are very limited for these cities and therefore are not used in the final specification).
Houses generally sell for more than other types of detached or semi-detached dwellings (Table 2). In each city, coefficient estimates on the dummy variables for cottages, semis, terraces, townhouses and villas are mostly negative and significant (detached houses are the omitted property type dummy). The coefficient estimates on the method of sale suggest that properties sold through an auction process (either before, at or after an auction) sell for slightly higher prices than houses sold through a private treaty (private treaty sales are the omitted sale method dummy). However, since the decision regarding sale method is endogenous, this effect most likely reflects a positive correlation between the sale method and the quality of the house.
Finally, it seems that the estimates of pure price changes (as measured through the time dummy coefficients) are quite robust to variation in the specification. Reverting to a much larger sample of data where information on postcode, property type, sale method, and land size are available, we can see that omitting some of the key characteristic variables (with the exception of postcode) makes little difference to the pure price change estimates (Figure 1).[16]
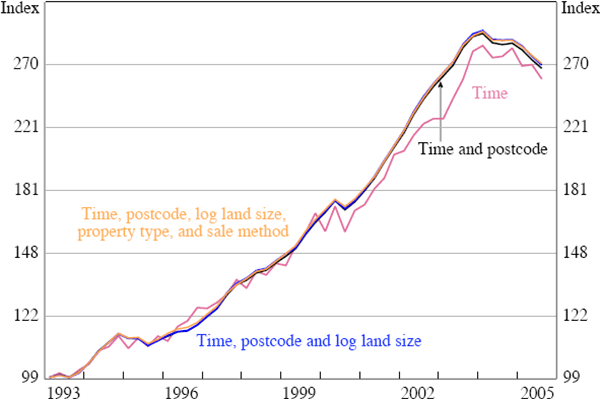
Note: Based on a sub-sample of approximately 500,000 observations.
Sources: APM; author's calculations
4.3 Repeat-sales Measures
I now estimate alternative repeat-sales specifications, limiting the dataset to houses which have turned over at least twice in the sample period. Specifically, I compare the repeat-sales formulation in Equation (4), which is an equally-weighted geometric measure, with two alternatives proposed by Shiller (1991): an equally-weighted arithmetic measure; and a value-weighted arithmetic measure.[17] The equally-weighted geometric and arithmetic measures, by construction, give an equal weight to price changes in houses of different value. Each can be interpreted as an index of the value of a portfolio of housing with equal dollar amounts invested in houses of different value (the only difference is that the former uses geometric means in its formulation while the latter uses arithmetic means). In contrast, the value-weighted arithmetic index places a higher weight on price changes in more expensive houses. Accordingly, it can be interpreted as an index of the value of a portfolio which replicates the aggregate stock of housing.
While APM data can be used for both Sydney and Brisbane, REIV data must be used for Melbourne (since this allows repeat sales to be matched). For each of these three indices, I estimate a version without a constant (the base case), and another with a constant. In the case of the equally-weighted geometric measure these regressions are:
and:
Equation 8 is a modification proposed by Goetzmann and Spiegel (1995) where the constant (σ) is designed to capture the average of any non-temporal effects on prices growth. This may be a reasonable approximation if quality change is related to the act of resale rather than the length of the holding period.
Table 3 summarises the average rate of prices growth (defined as average annualised growth between March 1993 and September 2005), the root mean squared error (RMSE) of the estimated rates of prices growth, and the squared sample correlation (SSC). The RMSE provides a guide to the magnitude of the variability in house prices growth that cannot be explained by each of the models. It comprises both idiosyncratic variation – that variation in prices growth which cannot be explained by the model and is house-specific – and error, which is variation associated with imperfect data or misspecification (Case and Szymanoski 1995).[18] The SSC provides a gauge of the fit of the model – that is, the extent to which a high RMSE can be explained by idiosyncratic variation or, alternatively, a poor-fitting model.[19] In other words, a high value of the SSC indicates that the error associated with mismeasurement or misspecification is likely to be low relative to idiosyncratic error.
| Equally-weighted geometric |
Equally-weighted arithmetic |
Value-weighted arithmetic |
|
|---|---|---|---|
| Sydney – no constant | |||
| Prices growth(a) | 8.8 | 9.3 | 9.0 |
| RMSE | 25.2 | 25.4 | 25.4 |
| SSC | 49.0 | 48.8 | 48.4 |
| Sydney – constant | |||
| Prices growth(a) | 7.8 | 8.1 | 7.9 |
| RMSE | 25.1 | 25.4 | 25.7 |
| SSC | 49.1 | 48.8 | 48.6 |
| Constant | 5.1 | 5.4 | 11,960 |
| (p-value) | 0.00 | 0.00 | 0.00 |
| Melbourne – no constant | |||
| Prices growth(a) | 9.5 | 10.2 | 9.6 |
| RMSE | 25.5 | 25.6 | 25.5 |
| SSC | 54.1 | 54.0 | 54.0 |
| Melbourne – constant | |||
| Prices growth(a) | 8.5 | 8.8 | 8.7 |
| RMSE | 25.3 | 25.7 | 25.7 |
| SSC | 54.1 | 54.0 | 54.1 |
| Constant | 5.1 | 5.7 | 7,675 |
| (p-value) | 0.00 | 0.00 | 0.00 |
| Brisbane – no constant | |||
| Prices growth(a) | 7.8 | 8.4 | 8.1 |
| RMSE | 25.5 | 25.7 | 25.7 |
| SSC | 50.7 | 50.0 | 49.4 |
| Brisbane – constant | |||
| Prices growth(a) | 6.0 | 6.3 | 6.3 |
| RMSE | 25.0 | 26.1 | 26.3 |
| SSC | 51.3 | 51.0 | 50.7 |
| Constant | 8.6 | 10.3 | 12,873 |
| (p-value) | 0.00 | 0.00 | 0.00 |
|
Notes: APM data are used for Sydney and Brisbane. REIV data are used for
Melbourne. All figures are percentage point terms except for the p-values, which
are probabilities, and the value-weighted arithmetic constant, which is a
measure of the average increase in the price level associated with non-temporal
quality change. Sources: APM; REIV; author's calculations |
|||
The three measures are remarkably similar in terms of their RMSE and SSC statistics. The average RMSE is around 25 per cent for all cities. This compares to an average price change of around 43 per cent for Sydney, 42 per cent for Melbourne (using REIV data) and 35 per cent for Brisbane. The average SSC is around 50 per cent for all cities, which implies that approximately half of the variation in prices growth is common across houses and half is idiosyncratic.
The similarities in the RMSE and SSC statistics for the different repeat-sales measures confirm that the repeat-sales estimator chosen does not have a large effect on model fit. There is, however, some (typically small) difference in the average prices growth inferred. The equally-weighted arithmetic measure generally points to higher prices growth than the equally-weighted geometric measure and the value-weighted arithmetic measure, implying that prices of high-value houses grew less, on average, than other houses between 1993 and 2005.
The data reject the hypothesis that the constant should be excluded in the repeat-sales regression for all cities. The positive estimates of the constant imply that the pure price changes have been lower than suggested by actual prices. The estimated value of the constant suggests that non-temporal price change is around 5 per cent for Sydney and Melbourne and around 9 per cent for Brisbane. However, the improvement in model fit associated with the inclusion of a constant is small.
4.4 Comparing Preferred Hedonic and Repeat-sales Measures
I now compare the hedonic and repeat-sales specifications. For the hedonic regression, I use a restricted specification with implicit price relativities set to be equal for both single and repeat sales (γt = 0) and constant over time (βt = β).[20] Although this restricted specification is rejected by the data, it is the simplest, is commonly used and, more importantly, makes no difference to the estimates of the pure price changes. For the repeat-sales measure, I use the equally-weighted geometric measure without a constant (see Equation (7)), since this is conceptually closest to the preferred hedonic measure.
The first two columns of Table 4 report the RMSE and SSC comparing estimated price changes with the actual price changes for each house in the repeat-sales sample (single sales are excluded). The RMSE statistics are very close for both the hedonic and repeat-sales regressions, and indeed very similar across cities, at around 25 per cent. Similarly, the SSC statistics are close with approximately 50 per cent of the variation in prices growth in the repeat-sales sub-sample explained by each of the models. These results suggest that using either a restricted hedonic approach, which controls for postcode, property type and sale method, or a repeat-sales measure is broadly equivalent in terms of model fit.
| Comparison of actual and fitted growth rates (RS) | Comparison of actual and fitted log prices (RS v AS) | ||||
|---|---|---|---|---|---|
| RMSE (percentage points) |
SSC (per cent) |
RMSE (per cent) |
SSC (per cent) |
||
| Sydney | |||||
| Hedonic (RS) | 25.3 | 49.0 | 28.4 | 80.2 | |
| Repeat-sales (RS) | 25.2 | 49.0 | na | na | |
| Hedonic (AS) | 25.3 | 48.8 | 30.0 | 77.9 | |
| Melbourne | |||||
| Hedonic (RS) | 25.7 | 53.9 | 32.4 | 72.3 | |
| Repeat-sales (RS) | 29.4 | 44.9 | na | na | |
| Hedonic (AS) | 25.8 | 53.8 | 32.7 | 72.3 | |
| Brisbane | |||||
| Hedonic (RS) | 25.6 | 49.9 | 33.5 | 62.4 | |
| Repeat-sales (RS) | 25.5 | 50.7 | na | na | |
| Hedonic (AS) | 25.6 | 50.3 | 35.1 | 59.1 | |
|
Notes: All statistics are calculated using data between the March quarter 1993 and the September quarter 2005. APM data are used for Sydney and Brisbane. REIV data are used for Melbourne. RS uses the repeat-sales sub-sample for estimation and AS uses the full sample (including single sales) for estimation. Sources: APM; REIV; author's calculations |
|||||
I also consider whether the inclusion of single sales, which may have different idiosyncratic price variability than repeat sales, can influence the fit of the restricted hedonic model. The final two columns of Table 4 show that the RMSE is higher and the SSC is lower when including single sales in the restricted hedonic model. This confirms that single sales are harder to predict and exhibit more idiosyncratic variation than repeat sales. Consistent with the previous findings, estimates of the pure price changes inferred from the restricted hedonic and repeat-sales approaches are very similar. Using Sydney as an example (Figure 2), estimates of pure price changes are remarkably similar for both measures, even though repeat-sales exclude all single sale information. This seems to imply that, when using very large samples, theoretical concerns regarding the most appropriate specification may not be as much of a problem empirically as studies that use smaller samples of data suggest.
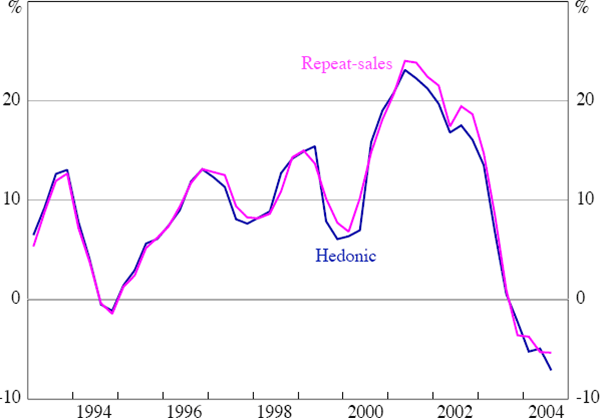
Sources: APM; author's calculations
4.5 Regression-based and Non-regression-based Measures
I also compare the preferred hedonic and repeat-sales measures of pure price changes with a mix-adjusted approach developed by Prasad and Richards (2006) and a simple median. The results using APM data for the three cities are shown in Figure 3. They demonstrate that there are noticeable differences between the median and the more advanced measures (hedonic, repeat sales and mix-adjusted), suggesting that adjusting for the composition, and to a much lesser extent, quality of properties sold, may provide better estimates of pure house price changes.
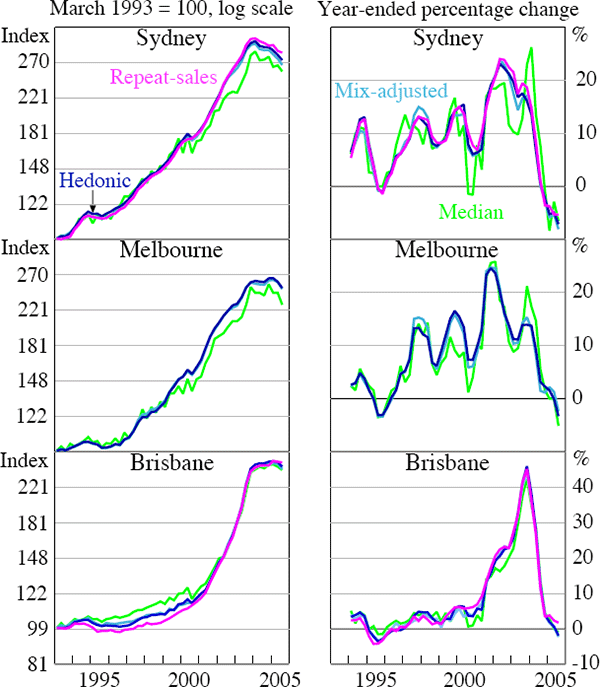
Sources: APM; author's calculations
Focusing on Sydney, there is substantially less variability in the regression-based measures when compared with the median, which points to much larger short-term swings in prices growth. Further, since the timing of turning points in the median does not always coincide with those inferred from the more complex measures, there appears to be several situations in which these measures have provided more consistent signals of the direction of pure house price changes. There is a strong similarity between the hedonic, repeat-sales and mix-adjusted measures. This suggests that a simple stratification-based approach can produce qualitatively similar results to regression-based approaches, which adjust for compositional and limited quality change (see Section 4.6 for further discussion of quality change).
Similar results are observed for Melbourne, although a repeat-sales measure cannot be constructed for this city using APM data. Repeating the exercise using REIV data, which permit the construction of repeat-sales, provides a similar picture (see Appendix D). The regression-based measures are comparable, whereas the median appears to underestimate pure price changes. For Brisbane, the median price index is somewhat closer to the regression-based pure price indices. Even so, there are still periods of noticeable divergence. The more advanced measures of pure price changes provide higher estimates of average annual growth than the median for Sydney and Melbourne (Table 5). Over the full sample, this amounted to a 0.6 and 1.2 percentage point difference in average annual growth between the advanced measures and the median for Sydney and Melbourne (using REIV data) respectively. This may have been due to an increase in turnover in lower-value postcodes, usually the outer suburbs, where new additions to the housing stock have become more prevalent in recent years. This does not appear to be as prominent in Brisbane, however, where the average annual growth of the more advanced measures is only slightly higher than that of the median.
| Average annual growth(a) | Standard deviation(b) | |
|---|---|---|
| Sydney | ||
| Median | 7.84 | 4.35 |
| Mix-adjusted | 8.16 | 2.33 |
| Hedonic | 8.39 | 2.26 |
| Repeat-sales | 8.76 | 2.21 |
| Melbourne(c) | ||
| Median | 8.01 | 5.23 |
| Mix-adjusted | 8.72 | 2.52 |
| Hedonic | 9.44 | 2.45 |
| Repeat-sales | 9.50 | 2.53 |
| Brisbane | ||
| Median | 7.41 | 3.23 |
| Mix-adjusted | 7.46 | 3.09 |
| Hedonic | 7.57 | 3.14 |
| Repeat-sales | 7.78 | 3.04 |
|
Notes: (a) Average effective annual growth between the March quarter 1993 and the
September quarter 2005. Sources: APM; REIV; author's calculations |
||
A comparison of the standard deviations of quarterly growth rates of alternative approaches suggests that the regression-based measures of pure prices tend to be smoother than the median, on average. Specifically, the average standard deviation of the hedonic and repeat-sales measures is approximately half the standard deviation of the median for Sydney and Melbourne (using REIV data). The decline in the standard deviation is much smaller for Brisbane with the average standard deviation of the regression measures only marginally below that of the median. It is also possible to examine whether the various measures constructed are different in a statistical sense – that is, whether there is any overlap between the confidence intervals of the level of each measures' index constructed at the 95 per cent level of significance.[21] Table 6 reports the proportion of the sample over which the various measures are statistically different. For all cities, the median is, on average, statistically different to the more advanced measures for at least half of the sample. In contrast, the more advanced measures tend to be more similar, as there are fewer periods where the measures are statistically different.
| Median | Mix-adjusted | Hedonic | Repeat-sales | Average CI width(a) |
|
|---|---|---|---|---|---|
| Sydney | |||||
| Median | 0.00 | 4.25 | |||
| Mix-adjusted | 0.42 | 0.00 | 7.84 | ||
| Hedonic | 0.58 | 0.00 | 0.00 | 3.21 | |
| Repeat-sales | 0.68 | 0.16 | 0.34 | 0.00 | 3.99 |
| Average(b) | 0.56 | 0.19 | 0.31 | 0.39 | 4.82(d) |
| Melbourne(c) | |||||
| Median | 0.00 | 5.02 | |||
| Mix-adjusted | 0.16 | 0.00 | 11.15 | ||
| Hedonic | 0.90 | 0.48 | 0.00 | 7.21 | |
| Repeat-sales | 0.82 | 0.62 | 0.02 | 0.00 | 11.94 |
| Average(b) | 0.63 | 0.42 | 0.47 | 0.49 | 8.83(d) |
| Brisbane | |||||
| Median | 0.00 | 3.47 | |||
| Mix-adjusted | 0.28 | 0.00 | 8.27 | ||
| Hedonic | 0.68 | 0.00 | 0.00 | 2.89 | |
| Repeat-sales | 0.76 | 0.16 | 0.50 | 0.00 | 3.00 |
| Average(b) | 0.57 | 0.15 | 0.39 | 0.47 | 4.41(d) |
|
Notes: Calculated using the 95 per cent level of significance between the June
quarter 1993 and the September quarter 2005. Sources: APM; REIV; author's calculations |
|||||
These results are consistent with findings from previous Australian studies that are based on smaller geographic regions. Specifically, using Port Pirie (South Australia) as a case study, Rossini et al (1995) find large differences in the annual prices growth of a median when compared with a hedonic measure and a repeat-sales median. Similarly, Costello (1997) shows, using strata title property for Scarborough (Western Australia), that hedonic and repeat-sales regressions provide better estimates of pure price changes than a mean or median, though he emphasises the importance of choosing a correct regression relationship. My findings suggest, at least for very large samples, that specification, while not inconsequential, is a second-order issue (so long as there is some control for compositional change). Flaherty (2004) uses house sales data for 10 Melbourne suburbs (Victoria) and finds that a hedonic index, estimated separately for each suburb, is significantly different from the median or mean for each suburb.
4.6 Quality Change
Figure 3 demonstrates that the hedonic, repeat-sales (without a constant) and mix-adjusted measures are all quite similar. This may be somewhat surprising because the hedonic measure is constructed, in principle, so as to control for quality change over time while the other two measures are not. It is likely, however, that the hedonic measure shown may not be adjusting adequately for quality change given the limited information on characteristics it includes (that is, postcode, property type and sale method).
To explore this further, I examine whether the pure price estimates from a hedonic specification that uses all available data on quality are different from the hedonic specification shown in Figure 3. Using a common sample, the results suggest that controlling for additional characteristics (namely, log land size, bedrooms, bathrooms and zoning) leads to higher estimates of pure prices growth (about 0.9 percentage points per annum for Sydney, 0.5 percentage points per annum for Melbourne and 2 percentage points per annum for Brisbane). On face value, this result implies that overall quality has actually fallen over the sample period. It appears, for the relatively small Sydney sample where complete data on quality are available, that on average, across all postcodes, the number of bedrooms and bathrooms of houses sold has declined from the first half to the second half of the sample period (a similar decline can be observed in the average number of bedrooms across postcodes in Melbourne). Whether such a result reflects actual quality change or a shift in the types of properties sold (compositional effects), and whether it would hold for larger samples of data and over other features of quality is unclear.
An alternative way to account for quality change is to include a constant in the repeat-sales regression. Based on previous estimates (see Table 3), non-temporal quality change is estimated at around 5 per cent for Sydney and Melbourne and around 9 per cent for Brisbane (using the equally-weighted geometric repeat-sales measures). Using the average rate of turnover for resales (around 15 quarters for Sydney and 14 quarters for Melbourne and Brisbane), this would suggest a quality-related price increase over the sample period of around 1.3, 1.4 and 2 per cent per annum for Sydney, Melbourne and Brisbane respectively. In comparison, repeat-sales estimates of pure prices growth from the same regressions amount to 7.8, 8.5 and 6.0 per cent per annum respectively for the three cities (Table 3).
Footnotes
I would like to thank APM and REIV for their assistance in providing these data. [9]
APM definitions are used for the regions covered. [10]
The results are qualitatively similar if additional characteristics such as log land size, and a smaller sample, are used. [11]
A repeat-sales dummy could not be constructed for Melbourne using APM data. To overcome this, I use REIV data for testing the implicit prices of single-and repeat-sales characteristics for Melbourne. [12]
Results are available from the author on request. [13]
To include as many attributes as possible meant using relatively small sub-samples (see notes in Table 2). Results are generally robust to more parsimonious specifications which excluded, in turn, zoning, bathrooms, bedrooms and sale type as explanatory variables. [14]
The standard deviation of the log land size in the median postcode is 0.38 for Sydney, 0.45 for Melbourne and 0.52 for Brisbane. [15]
Although this result cannot be generalised to the full sample using all characteristics data for Sydney (postcode, property type, sale method, land size, bedrooms, bathrooms, zoning), it does hold for the characteristics that are available for the full sample, which include postcode, property type and sale method; the same is true for Melbourne and Brisbane. [16]
For an overview of the construction of these indices see Appendix C. [17]
For a more thorough discussion of the use of regression diagnostics in comparing different approaches to house price measurement, see Case and Szymanoski (1995) and Crone and Voith (1992). [18]
In models with a constant, the SSC is equivalent to the unadjusted R2. [19]
The characteristic variables used in the restricted hedonic regression include postcode, property type and sale method because these data are available for the full sample. The results are similar if additional characteristic variables, such as log land size, are included and a smaller sample is used. [20]
For further discussion of the construction of the confidence intervals for each measure, see Appendix A. [21]