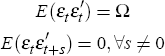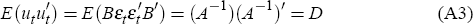RDP 2005-06: Credit and Monetary Policy: An Australian SVAR Appendix A: The SVAR Methodology

This appendix briefly outlines the structural vector autoregression (SVAR) methodology. For a more detailed exposition, the reader is referred to Chapter 11 of Hamilton (1994). Consider the following reduced-form representation of the system:

where:

X_t is a vector of macroeconomic variables, C is a polynomial function of order p and L is the lag operator.

Now consider a square matrix T such that (T⁻¹)(T⁻¹)′ = Ω, so TΩT′ = I, the identity matrix.^[10] Define T = AB, where A is diagonal and B's diagonal contains only ones. The matrix A has the same lead diagonal as T, but zeros elsewhere, while B is formed by dividing each row of T by the lead diagonal element of that row. Multiplying Equation (A1) by B gives the structural VAR representation:

where the matrix B is the contemporaneous relationships between the variables and Bε_t = u_t. The covariance matrix of the errors from Equation (A2) is given by:

Note that because A is diagonal, so too is D. Therefore, u_t can be interpreted as a vector of structural shocks, defined as a shock to a particular variable that is orthogonal to other shocks in the economy. In the reduced form, that is Equation (A1), the disturbances, ε_t, could be the result of structural shocks to other variables. For example, unexpected changes to the exchange rate could be caused by contemporaneous disturbances to, say, the interest rate. The matrix B filters the reduced form shocks so that the structural shocks can be identified.

The matrix B can be solved for by first running the VAR represented in Equation (A1) to obtain an estimate of Ω. From this estimate, B and A can be calculated from the equation ((AB)⁻¹)((AB)⁻¹)′ = (T⁻¹)(T⁻¹)′ = Ω if sufficient restrictions are imposed on these two matrices. Suppose that there are k variables in the system, so there are k² degrees of freedom in A and B. Because Ω is a symmetric matrix, there are only 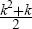unknowns, so at least 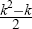restrictions need to be imposed. These restrictions typically, but not always, take the form of restricting B's off-diagonal elements to be equal to zero, and as such constitute restrictions on the contemporaneous affect of one variable on another. Some studies choose a Choleski decomposition of Ω, resulting in a temporal ordering of the variables. This is referred to as a recursive VAR. An alternative, followed here, is to allow a more elaborate set of restrictions guided by economic theory. This is referred to as a SVAR.

Footnote

This can be done if the random shocks are linearly independent. Consider any conformable non-zero vector 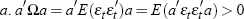, and so Ω is positive definite, thus invertible, and therefore there exists at least one such matrix, T. [10]