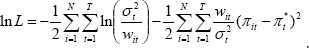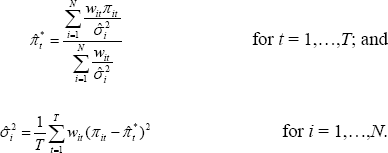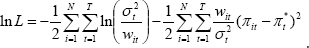RDP 2005-05: Underlying Inflation: Concepts, Measurement and Performance Appendix: Derivation of Underlying Inflation Estimators

First, we show how to derive the double-weighted measure described by Laflèche (1997) as a maximum likelihood estimator of underlying inflation, along similar lines to Diewert's (1995) derivation of the neo-Edgeworthian measure. The model is defined by the equation:

Assume that E(ν_it)=0 and 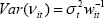, for i = 1,…, N and t = 1,…,T. Assuming further that we are sampling from a normal distribution, the log-likelihood function for this model, aside from a constant, is:

Partially differentiating with respect to 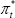and 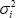, and setting the resulting expressions equal to zero, yields the following system of T + N simultaneous equations that can be used to determine the maximum likelihood estimators for the model:

Note that the formula for 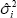multiplies relative price inflation at each point in time by the effective expenditure weight, and thus does not correspond to the usual notion of a variance.

Similar measures have been proposed before (for example, Laflèche 1997, Marques et al 2000, Aucremanne 2000), but by using the reciprocal of the sample standard deviation they only approximate this estimator. The neo-Edgeworthian measure is usually constructed in a similar ad hoc manner, although it has been more rigorously estimated as the solution to a full system of equations for the US and for the euro area by, respectively, Wynne (1997) and Vega and Wynne (2003). Regular breaks in the Australian CPI would make precise estimation of either the double-weighted or neo-Edgworthian measure difficult in the Australian context.

Second, we derive the weighted mean of the distribution of price changes, in the spirit of Clements and Izan (1987). One could also do this for the trimmed distribution of price changes, assuming that the trimmed price changes are simply outliers that have been ‘cleaned’ from the data. In the Australian case, this could make the assumption that we are sampling from a normal distribution more defensible. The model is comprised of Equation (A1) and the assumptions that E(v_it) = 0 and 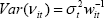. The only difference compared with the previous model is that now 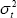is assumed to be common to all goods and services. This time, the log likelihood function is:

Differentiating with respect to 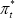and setting the partial derivative equal to zero, we have:

Since 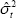cancels out, the maximum likelihood estimator for the systematic component of inflation is: