RDP 2004-09: Co-Movement of Australian State Business Cycles Appendix C: Gross State Product and Hours Worked

David Norman and Thomas Walker

October 2004

In our modelling we used SFD as a proxy for state output. As discussed in Section 2, SFD effectively excludes trade and changes in inventories, yet trade flows might be expected to capture the bulk of spillover effects between states. It would be preferable to use a measure of gross state product (GSP) which captures these effects. Since the ABS ceased calculating and reporting quarterly GSP estimates in June 1997, we construct our own estimates of quarterly GSP from annual data, to assess whether including trade increases the role given to spillovers in the model.

We apply the ordinary least squares method detailed in Chow and Lin (1971), using the quarterly profile of SFD to interpolate quarterly GSP estimates from the ABS's annual GSP series.[26] Compared with the ABS quarterly series available over the period 1985:Q3–1997:Q2, the constructed series matches medium-term movements in GSP moderately well (year-ended growth rates of the two sets of estimates have correlations of about 0.7), but quarterly growth rates only marginally (correlations of around 0.3). Since the ABS emphasised the experimental nature of its constant price quarterly GSP estimates, there is no absolutely reliable benchmark, but we feel it is worth examining the effects of using our constructed measure of GSP in place of SFD in the model.

Full results are presented below. The main point to note is that most of the results for this specification are very similar to those from the model using SFD and hours worked. The estimated common cycles of the two models are almost identical, and the trend and common cycle response parameter estimates for GSP (Table C2) are much the same as those for SFD. On the whole, the change does not appear to alter the main characteristics of the model. This may be due in part to the fact that the quarterly profiles of the constructed GSP series and SFD are by definition very similar.

The cumulative state responses to common and idiosyncratic shocks for the GSP-hours worked model are presented in Table C1. Using GSP does not substantially alter our assessment of the importance of spillovers. The response of WA to NSW is much more reasonable than in Table 5, but its response to the national cycle is larger. Most of the other responses remain broadly the same size. The off-diagonal elements are larger than in Table 5, but not significantly larger. Except for Tasmania's response to NSW and WA's response to Tas, all of the off-diagonals are smaller than their diagonal counterparts. Once again, this suggests that spillovers are less important than idiosyncratic shocks, but may nevertheless be of some significance in determining activity.

Table C1: Cumulative Responses to Shocks
Gross state product
State Cumulative effect after eight quarters of a shock to:
  NSW Vic Q1d WA SA Tas National
NSW 3.5 −0.2 −1.2 −0.6 −1.1 −0.6 5.5
Vic 1.7 3.0 0.0 0.0 −1.5 −0.8 5.6
Q1d 0.6 0.6 2.8 1.5 0.7 1.4 7.2
WA 1.4 2.8 2.9 3.7 2.4 4.2 9.6
SA −2.6 −1.9 −1.6 −1.5 2.1 −2.3 5.6
Tas −3.9 −2.7 −1.2 −1.3 0.0 1.3 4.4

Notes: The cumulative response is effectively the integral between the shocked level of GSP and the no-shock counterfactual level from the shock quarter to the eighth quarter following the shock. The shocks to state idiosyncratic cycles are all 1.0 per cent; the shock to the common cycle is 0.89 per cent (see notes to Table 5). All shocks last one quarter, but the model dynamics imply a sustained decay path in each case.
Table C2: Estimated Parameters for Gross State Product
State Trend parameter, δg Common cycle response
parameter, γg
  1985:Q4–1994:Q4 1995:Q1–2003:Q2
NSW 2.54 3.68 1
Vic 1.88 4.02 1.01
Q1d 4.36 4.57 1.31
WA 4.67 3.55 1.76
SA 1.45 2.75 1.03
Tas 0.95 1.56 0.81
National average 2.76 3.80 1.13

Notes: Trend parameter estimates can be interpreted as average annualised percentage growth rates. The national cycle response parameter for NSW is normalised to be 1. The ‘national average’ figures are calculated as the average of the state figures, weighted by their share of total GSP.
Table C3: Estimated ρ and θ Parameters
Common cycle coefficient, ρ 0.93
Common cycle error variance, 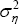Inline Equation 5.8×10−5
State Idiosyncratic cycle response
coefficient, θi (for hours worked)
NSW 0.41
Vic 0.41
Q1d 0.22
WA 0.07
SA 0.18
Tas 0.48

Notes: Sample is 1985:Q3–2003:Q2, yielding 71 observations. Idiosyncratic response coefficients for GSP are constrained to equal 1.
Table C4: Idiosyncratic Cycle Equation Coefficients, Φ as
State NSW Vic Q1d WA SA Tas
NSW 0.67 −0.07 −0.22 −0.06 −0.14 −0.07
Vic −0.04 0.49 −0.13 −0.12 −0.27 −0.23
Q1d −0.17 −0.29 0.24 0.15 −0.20 −0.17
WA 1.03 1.29 1.35 1.11 0.94 1.15
SA −0.41 −0.32 −0.34 −0.24 0.49 −0.28
Tas −0.50 −0.42 −0.32 −0.22 −0.16 0.45

On the whole, using an approximate measure of GSP in place of SFD in our model does not appear to change our earlier conclusions. Gauging the precise details of the effects of spillovers remains very difficult given the approximate nature of our GSP estimates and the small sample size.

Footnote

This method involves estimating a simple linear regression of annual GSP on annual SFD, allowing for serial correlation in the error term. We then use the estimated coefficients to generate quarterly estimates of GSP from the quarterly SFD data. Finally, in order to satisfy an annual adding-up constraint, the serial correlation relationship is used to generate quarterly predictions of the error terms, which are added to the quarterly GSP predictions. Further details can be found in Chow and Lin (1971). [26]