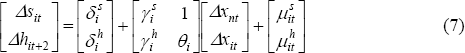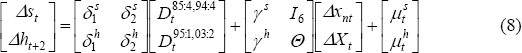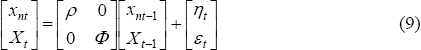RDP 2004-09: Co-Movement of Australian State Business Cycles 4. An Unobserved Components Model

4.1 Background

The results presented in the previous sections offer an insight into the patterns of cyclical activity in Australia, the degree of co-movement between state cycles, and the possible importance of different types of shocks. These simple measures may explain the extent to which economic activity in one state co-moves with activity in another, but they cannot determine how states respond to different types of shock, or where these shocks come from. They may also give an exaggerated impression of the economic interdependence of states, to the extent that state data contain a large component of activity common to all states and driven by external factors. Finally, the smoothness of the band-pass filtered data may lead to higher correlations than is plausible. In this section we introduce an unobserved components model, which attempts to disentangle the many sources of cyclical fluctuation, and determine how these fluctuations trace their way through the economy.^[12]

Our approach is a variation on that used by Kouparitsas (2002), which in turn is based on work by Watson (1986). In his analysis of US regional activity, Kouparitsas studied quarterly per capita income from 1961:Q1 to 2000:Q4. Unfortunately, quarterly SFD for Australia is only available back to the mid 1980s, yielding around 70 observations. Given the number of parameters to be estimated, we reconfigure the model to use both SFD and hours worked simultaneously. The benefits of this adjustment are twofold. First, by restricting SFD and hours worked to respond (in the latter case with a lag) to the same common and state-specific cycles, we increase the degrees of freedom by doubling the number of observations while less than doubling the number of coefficients. Second, the augmented model produces extracted cycles which can be considered a compromise between the fluctuations in labour market and income-based measures of activity (with hours worked also capturing developments in the traded sector, which SFD excludes). This compromise is consistent with Burns and Mitchell's (1946) definition of business cycles as patterns observed across a range of economic data, and hopefully makes our results more robust.

Data on SFD and hours worked for the six states are available quarterly from 1985:Q4–2003:Q4. Growth in domestic final demand has its highest correlation with growth in total hours worked at a lag of two quarters, so we lag hours worked by two quarters in the model.^[13] This reduces the sample to 1985:Q4–2003:Q2, or 71 observations.

4.2 Specification

This section outlines the methodology and basic structure of the model. It is an example of the class of general dynamic multiple-indicator, multiple-cause (DYMIMIC) models pioneered by Watson and Engle (1983), which characterise observed economic activity as a function of observed and unobserved variables. We assume the level of state activity (for either SFD or hours worked) can be specified as the sum of state-specific trend and cyclical components:

where y_it is the log of either measure of activity in state i, and τ_it and c_it are state-specific trend and cycle components. Following Beveridge and Nelson (1981), we assume that the trend level of activity is characterised by a random walk with drift, as shown in Equation (3):^[14]

The drift parameter δ_i is state-specific, allowing states to grow at different trend rates. Although not shown in Equation (3), we add a structural break in the trend growth rate after 1994:Q4, to capture structural changes in the economy following the recession.^[15] The cyclical component for state i is assumed to be driven by two unobservable cycles: a common national cycle, x_nt, and an idiosyncratic cycle, x_it, as shown in Equation (4):

The parameter γ_i governs the magnitude of the response of activity in state i to the common cycle, and is allowed to vary across states. This means that the amplitude of the common cycle effect on each state's activity may vary, but its shape and timing is identical for all states. The common cycle is assumed to be an AR(1) process:^[16]

where η_t, the common shock, is normally distributed with mean zero and variance 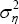. The idiosyncratic cycles are modelled as a VAR, with each idiosyncratic cycle specified as a function of the first lags of all six idiosyncratic cycles:

where the ε_it, the state-specific (or idiosyncratic) shocks, are normally distributed with mean zero and variance σ_i². Idiosyncratic shocks in each period are assumed to be uncorrelated both across states and with the common shock. We assume that all shocks are uncorrelated across time.

Note that, in this framework, idiosyncratic and common shocks are distinguished by the fact that common shocks affect all states simultaneously, while idiosyncratic shocks affect only the state of origin in the quarter of the shock. However, idiosyncratic shocks may subsequently spill over to other states' cycles. Our framework therefore allows for three sources of cyclical disturbance to the level of state activity: common shocks, idiosyncratic shocks, and spillovers of shocks between states.

Because all series are non-stationary, we model SFD and hours worked in first differences of the log levels.^[17] The estimated equations (for each state i) are:

where the superscripts s and h denote coefficients pertaining to SFD and hours worked. In state-space form, this can be represented by the measurement equations:

and transition equations:

where 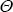is a 6×1 vector of the θ_i coefficients, and φ is a 6×6 vector of the ϕ_ij response coefficients. Note that SFD and hours worked respond to the same common and idiosyncratic cycles, but hours worked responds with a two-quarter lag.^[18] The variables μ_it are error terms, containing the trend innovations and noise (such as measurement error) not captured by the common or idiosyncratic cycles. These errors are assumed to be normal with zero mean and constant variance. All error terms in the model are assumed to be independent across time, states and equations. We estimate the system of Equations (8) and (9) as a Kalman filter, using Watson and Engle's (1983) two-step EM algorithm.^[19]

Footnotes

VAR models are also often used in the literature to explore business cycle co-movement (see, for example, Labhard 2003), but consume too many degrees of freedom, and are unable to distinguish clearly between common and idiosyncratic shocks when the data are relatively smooth. [12]

A lag of roughly two quarters is also apparent from a visual comparison of the band-pass filtered cycles for SFD and hours worked (Figure 2). [13]

Tests indicated the presence of a unit root in all states for both SFD and hours worked. We therefore model activity as the sum of a non-stationary trend and a stationary cycle. [14]

We experimented with various locations for the trend break, and a break after the 1990 recession was found to be most successful in fitting the data and ensuring the estimated cycles were stationary. Our results are not sensitive to the exact location of the break, but we chose the end of 1994 as a point sufficiently past the end of the recession period yet close to the middle of our sample. [15]

Cycles are generally modelled as AR(2) processes, including by Kouparitsas (2002). We found that allowing a common cycle to be AR(2) did not materially change our results, so we used a simpler AR(1) process for parsimony, given our small sample size. It may be that the inclusion of two observed series, one with a two-period lead, provides the second eigenvalue necessary for the observed cyclical behaviour. [16]

The Kalman filter requires all dependent variables to be stationary. It would also be feasible to use as the dependent variable a detrended series, such as band-pass filtered SFD, or a year-ended growth rate. We use the first difference here because it produces a well-behaved error term, obviating the need for a more complicated specification. [17]

The parameters γ_t and θ_i allow SFD and hours worked for each state to respond with different amplitudes to the common and their own idiosyncratic cycles. For identification purposes, SFD is assumed to respond one-for-one to its idiosyncratic cycle, and 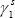(the responsiveness of NSW SFD to the common cycle) is set equal to one. [18]

We impose a convergence criterion of 1×10⁻⁴ on the sum of squared deviations of the parameters and unobserved components from their previous iteration levels. We found the results to be insensitive to the exact criterion and starting points used. See Hamilton (1994) for more information on this methodology. [19]