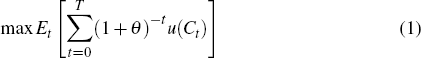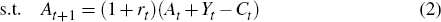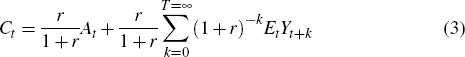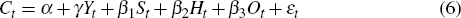RDP 2003-07: Housing Wealth, Stock Market Wealth and Consumption: A Panel Analysis for Australia 3. Theoretical Considerations and Model Specification

Although the focus of this paper is empirical, we want to ensure that our chosen specification is consistent with standard consumption theories. In the next subsection we briefly discuss an empirical model based on the Life-Cycle/Permanent Income Hypothesis (LC-PIH) of consumption, which links consumption to income and wealth. We then introduce the specification chosen for Section 4.

3.1 Theoretical Considerations

Our model is based on a standard textbook LC-PIH model as described in Blanchard and Fisher (1989). A representative consumer chooses the path of consumption C_t to maximise (expected) utility u_t over her life time, where θ is the rate of time preference (Equation (1)). In each period, the budget constraint implies that assets at the end of the period A_t+1 equal savings (defined as labour income Y_t plus assets at the beginning A_t minus consumption), which earn interest at the rate r_t (Equation (2)).

The first-order condition implies the following optimal consumption path:^[6]

Equation (3) expresses consumption at time t as a function of the assets in that time period (non-human wealth) and the sum of the current and discounted expected future income stream (human wealth). Note that in this model the marginal propensity to consume out of wealth is 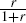. If for instance the long-run risk-free real interest rate was between 3 and 5 per cent, the MPC would be between 0.03 and 0.05. Of course, this result depends on the assumptions imposed to arrive at Equation (3), such as an infinite planning horizon and a constant, risk-free interest rate on assets. Assuming instead that the consumer has a remaining life span of 30 years rather than infinity (and if we rule out bequest motives), the MPC would increase to between 0.05 and 0.06, other things being equal.

If we further assume that income follows a stochastic AR(1) process with a coefficient η, we can express current consumption as a function of current assets and current income (Equation (4)), where β and γ are functions of r and η.

The consumption function in Equation (4) makes no distinction between the different assets an individual might hold. For simplicity, let us consider only two types of assets: stock market assets S_t (a financial asset) and housing wealth H_t (a non-financial asset). The consumption function then takes the form:

From theory, one might expect the marginal propensity to consume out of stock market wealth β₁ to be similar to that of housing wealth β₂. However, a number of reasons have been put forward for why the responsiveness of consumers to different types of wealth could be different: differences in liquidity, other utility associated with owning an asset (housing services, bequest motives), distribution across income groups, expected permanency of changes, mismeasurement of wealth and ‘psychological factors’.^[7]

First, the two classes of assets may have differences in liquidity^[8]. For instance, housing is often considered a ‘lumpy’ asset – it may be difficult to liquidate only a part of it, and transaction costs of ‘trading up’ or ‘trading down’ tend to be high. In contrast, it might be easier to change stock market wealth by buying or selling a small number of shares. This implies that the coefficient on housing wealth should be lower than that on stock market wealth. However, financial innovation, such as the availability of home equity loans, is likely to have increased the liquidity of housing assets as can be seen by the increase in housing equity withdrawal in recent years (see Muellbauer and Lattimore (1999) and Reserve Bank of Australia (2003)).

Second, housing represents both an asset and a consumption item. When house prices increase, wealth may increase, but so too does the cost of housing services (see Poterba (2000)). Increases in the value of owner-occupied housing do not increase the ability of a household to consume more of other goods and services unless that household is willing to realise that increased value, say by ‘trading down’ into a smaller and less expensive house. Many households do not appear to be willing to do this, including those who intend to leave their houses as bequests^[9]. This factor makes it less likely that increased wealth in housing is consumed, resulting in a lower MPC from housing wealth.

Third, there may be distributional factors at work. Housing wealth tends to be held by consumers in all income classes. Stock market wealth, on the other hand, is in many countries concentrated in the high-income groups which are often thought to have a lower propensity to consume out of both income and wealth. In this case, changes in housing wealth might have a larger impact on consumption than changes in stock market wealth. This reason is often cited for why the stock market effect in European countries is often smaller than in the US, as US share ownership is spread more widely across the income distribution (see IMF (2000)).

Fourth, consumers may view increases in wealth for some asset classes as more likely to be permanent, while others are more likely to be viewed as temporary or uncertain. This difference in perception of the permanency of price changes could be related to past experiences of sudden price reversals in asset markets, such as stock markets or housing markets. If an increase (or decrease) is seen as permanent, it is more likely to increase (or decrease) long-run consumption.

Fifth, consumers may not find it easy to accurately measure wealth. This may be especially so for houses which are less homogenous and less frequently traded than shares. On the other hand, the argument has also been put forward that many consumers may not be aware of the exact value of their indirect share holdings, such as pension funds or superannuation funds, until they are close to retirement age.

Finally, consumers may attach certain psychological factors to certain assets. For instance, house ownership may also be an end in itself, as it provides a visible sign of status. Or as argued by Shefrin and Thaler (1988), consumers may use ‘mental accounts’ and earmark certain assets as more appropriate to use for current expenditure while others are reserved for long-term savings.

It is ultimately an empirical question which of these effects dominate, and thus whether the effect of housing wealth on consumption is different from that of stock market wealth. Before we discuss the empirical results of our attempt to estimate these effects, however, we have to clarify a number of specification issues.

3.2 Model Specification

Our chosen model specification is based on Equation (5), but it is augmented by a variable O_t measuring other wealth which captures the effect of financial assets not included in the stock market wealth variable (such as currency holdings, term deposits and non-equity superannuation holdings).

Theory might suggest that all the wealth variables should be measured as net wealth. Housing wealth is therefore measured net of housing debt, which accounts for between 60 and 80 per cent of household debt in Australia over the sample period. Stock market wealth is measured using the asset variable only. This reflects the lack of information on how much (if any) of households' personal debt is used to finance the purchase of stock market wealth. Finally, other wealth is defined to comprise all financial assets not captured in the stock market variable, net of households' personal debt^[10]. All variables are expressed in real per capita terms and the equation is estimated in levels.^[11]

At this point, we should stress that our focus in estimating Equation (6) is not to test a particular form of a consumption function, or to test the LC-PIH hypothesis. To do so one would ideally like to include a richer specification of dynamics which would no doubt substantially enhance its short-run forecasting performance. Our objective is instead to isolate and measure the effects of stock market wealth and housing wealth on consumption over a longer time horizon. Our interest lies therefore in the parameters β₁ and β₂ which measure the effect of stock market and housing wealth on consumption. Accordingly we treat income and other net wealth as control variables.

Another specification issue is whether to use total consumption or non-durable consumption in our model. Much of the earlier consumption literature (e.g., Blinder and Deaton (1985)) focuses on non-durable consumption. A justification for this is that these studies test the behavioural relationships based on the utility derived from the flow of consumption. Since the flow of services from durable goods is difficult to measure, durables are usually omitted.

In contrast, our focus is to measure the effect of changes in housing and stock market wealth on the aggregate economy. To this end we focus on consumption expenditure, which includes expenditure on durable goods, and we are less interested in consumers' utility from the flow of consumption. We therefore use total consumption.^[12]

Footnotes

This requires a number of assumptions, such as a quadratic utility function, the assumption that the interest rate r_t is constant and equal to the rate of time preference θ, the holding of the life-time budget constraint, an infinite horizon for optimisation and a no-Ponzi game condition, which rules out bequest motives for holding assets. [6]

For a more detailed discussion see Case et al (2001). [7]

For a more detailed analysis of the impact of asset liquidity on consumption, see Pissarides (1978). [8]

A related argument is based on the notion that for every household that sells a house there is a household that buys it. Therefore, in aggregate, the increase in consumption (through the seller) could be offset – at least partially – by a decrease in consumption by the buyer. For a model that formalises this argument, see Bajari, Benkard and Krainer (2003). [9]

We have also estimated a model which includes the debt terms separately. While our main results of a significant stock market and housing wealth effect survive, the stock market effect falls considerably and the housing wealth effect rises somewhat. However, several results of these specifications, such as a positive coefficient on housing debt, point towards econometric problems when estimating a large number of coefficients with highly correlated variables and a short sample size. [10]

The empirical literature is divided on whether consumption functions should be estimated in levels or logarithms; see the discussion in Lettau, Ludvigson and Barczi (2001) and Deutsche Bundesbank (2003). We follow the previous literature for Australia (e.g., McKibbin and Richards (1988), Debelle and Preston (1995), and Tan and Voss (2003)) and estimate Equation (3) in levels. In our model, the coefficients do not change substantially when estimated in logs and transformed into MPCs. [11]

This is also the approach chosen by Case et al (2001). Using total consumption also allows us to avoid a number of problematic issues. Firstly, if one is using non-durable consumption then for consistency one must include durables in wealth, which they (arguably) are not. Secondly, one must decide on some (necessarily ad hoc) depreciation rate to depreciate durable goods wealth. For a discussion and further justification see Rudd and Whelan (2002). [12]