RDP 2003-07: Housing Wealth, Stock Market Wealth and Consumption: A Panel Analysis for Australia 4. Estimation
July 2003
- Download the Paper 131KB
Studies that try to jointly estimate the effect of changes in housing wealth and stock market wealth often find that one of the coefficients is insignificant. More often than not this is the coefficient on housing wealth. But why is the housing wealth effect so elusive? One possible reason is that there is a high degree of correlation between aggregate housing wealth and stock market wealth, making it difficult to disentangle the two effects. This multicollinearity can cause one of the variables to appear insignificant.
In a recent study for the US, Case et al (2001) suggest that this multicollinearity between the two wealth variables could be mitigated using state-level data. Since each state's housing market is geographically distinct, each will be affected by regional shocks, in addition to national macroeconomic shocks. Thus the profile of housing wealth over time should differ from state to state. In contrast, stock markets are highly integrated across states so we would expect similar trends in the valuation of equity market portfolios across states.[13]
This variation in the state-level profiles of housing wealth should dampen the multicollinearity found in the aggregate level data. In addition, using a panel will increase our sample size relative to aggregate estimates. Thus state-level panel data should give us more accurate estimates of the housing and stock market wealth effects, allowing us to establish their size and significance and to test for a difference in magnitudes.
Before we proceed to discuss the estimation strategy and estimation results, we describe briefly how the state-level data set was constructed.
4.1 Data Summary
The data used in the estimation consist of a panel of observations on five economic variables. These variables are consumption, income, stock market wealth, net dwelling wealth and net other financial wealth. The cross-section spans five Australian states: New South Wales (NSW), Victoria (VIC), Queensland (QLD), South Australia (SA) and Western Australia (WA)[14]. We also have a similar data set for the nationwide aggregate. All series are quarterly observations from 1984:Q4 to 2001 :Q4. For some of the state-level series the quarterly profile had to be inferred for the earlier part of the sample using aggregate data. A detailed description can be found in Appendix A.
For consumption we use data on ‘household consumption expenditure’ which are available from the Australian Bureau of Statistics (ABS) on a quarterly frequency at the state level and an aggregate (nationwide) level.
The measure of labour income was constructed using earnings data adjusted for transfers and taxes, similarly to Tan and Voss (2003). The earnings data are calculated using a measure for the wage bill, scaled to account for self-employed persons. All these data are available on a state level.
Stock market wealth and other financial wealth is based on the ABS Financial Accounts from 1988:Q4 onwards. Foster (1997) provides data on household financial wealth prior to this. We use two measures of stock market wealth. The first includes both direct equity holdings and equity held through superannuation funds – the remaining financial assets are included in ‘other financial wealth’. As it is not clear how closely households monitor equity wealth held indirectly through superannuation funds, we use a second measure of stock market wealth that includes direct equity holdings only. For this version, equity superannuation wealth is included in ‘other financial wealth’. To obtain state-level data the aggregate level stocks are distributed among the states using financial flows data for the respective components from the 1994 Household Expenditure Survey (HES). We thus assume that the distribution of stock market wealth across states is constant through time.[15]
Dwelling wealth was constructed using median dwelling prices and the number of dwellings. We construct data on the number of dwellings for each state using the census and housing completions data. For dwelling prices we use the quarterly median dwelling price series from the Commonwealth Bank of Australia/Housing Institute of Australia (CBA/HIA), which is available on an aggregate and a disaggregate level[16].
Data on household debt are based on the quarterly series on aggregate housing debt and personal debt from the RBA. To obtain state-level series these data were distributed among the states using loan repayment flows for both categories of debt from the 1994 HES.
All variables are in per capita and in real terms, deflated by the relevant state consumption deflator.
4.2 Estimation Strategy
Our data panel is quite different from the typical panel in micro-econometrics in that the number of time periods is quite large. Moreover, our variables are non-stationary and cointegrated[17]. For this type of panel, Pesaran and Smith (1995) discuss a number of estimators that yield consistent estimates of the average effect across groups. These ‘average’ effects are more informative for monetary policy which is concerned with setting policy at an aggregate level, rather than at the state level.
First, the fixed-effects estimator is proposed. We estimate a standard fixed-effects model, but also an Instrumental Variables (IV) version which takes account of the endogeneity of the right-hand side variables.
A more sophisticated estimator is the panel dynamic OLS (panel DOLS) estimator. This is the panel equivalent of Stock and Watson's (1993) widely used dynamic OLS (DOLS) estimator. The DOLS estimator is a single equation technique that has better small sample properties than OLS and is able to deal with regressor endogeneity by the inclusion of lead and lagged differences of the explanatory variables. Many studies which estimate aggregate consumption functions favour the DOLS estimator[18]. Our panel DOLS estimator is equivalent to that developed in a recent study by Mark and Sul (2002). The estimator used is of a form that allows for fixed effects in the cointegrating regression, thus making it conceptually equivalent to the standard fixed-effects panel estimator.
Second, the mean group estimator is employed. This involves running separate regressions for each group, and averaging the coefficients across groups. We estimate the separate regressions for each group using a Seemingly Unrelated Regressions (SUR) estimator in its standard form (a Zellner GLS estimator) and in an IV version. We then average the coefficient to obtain the mean group estimator proposed by Pesaran and Smith (1995).[19]
Third, we estimate the consumption function using aggregate data. As this is not the focus of our paper we estimate the aggregate primarily to provide a benchmark (with the same specification) against which to compare our findings at the state level.
Pesaran and Smith (1995) point out that all these estimators provide consistent estimates of the average effect. However, due to the small cross-section dimension of our panel, some differences are to be expected.
4.3 The Fixed-effects Estimator
We present the results of the fixed-effects estimation in Table 1. The fixed-effects estimator is an OLS estimator that imposes common slopes, but allows for state-specific intercepts. In addition to the standard fixed-effects estimates the results of an Instrumental Variable (IV) estimator are reported, which corrects for the inconsistency of OLS arising from the endogeneity of income.[20]
| Variable | Description | All equity | Direct equity only | |||||
|---|---|---|---|---|---|---|---|---|
| OLS | IV | Panel DOLS | OLS | IV | Panel DOLS | |||
| Yt | Disposable income | 0.450* (0.042) |
0.565* (0.055) |
0.583* (0.083) |
0.456* (0.040) |
0.569* (0.051) |
0.623* (0.077) |
|
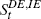 |
Stock market wealth (all equity holdings) |
0.024* (0.001) |
0.021* (0.002) |
0.023* (0.003) |
||||
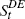 |
Stock market wealth (direct equity only) |
0.019* (0.003) |
0.015* (0.003) |
0.025* (0.006) |
||||
| Ht | Net housing wealth | 0.008* (0.001) |
0.007* (0.001) |
0.008* (0.001) |
0.008* (0.001) |
0.007* (0.001) |
0.008* (0.001) |
|
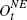 |
Net other financial wealth (excludes all equity) |
0.025* (0.002) |
0.023* (0.002) |
0.017* (0.003) |
||||
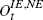 |
Net other financial wealth (excludes direct equity) |
0.026* (0.001) |
0.024* (0.001) |
0.020* (0.002) |
||||
| No of obs | 345 | 335 | 325 | 345 | 335 | 325 | ||
| No of groups | 5 | 5 | 5 | 5 | 5 | 5 | ||
| R2 within | 0.96 | 0.96 | ||||||
| R2 overall | 0.81 | 0.81 | ||||||
| F-test (fixed effects = 0) | 134 | 103 | 136 | 106 | ||||
|
Notes: All variables are in real per capita terms and in levels. Standard errors are in parentheses and * denotes significance at the 5 per cent level. For the IV estimations we use the first and second lags of income and contemporaneous values of the other independent variables as instruments. |
||||||||
As our model is estimated in levels, all the coefficients are interpreted as long-run MPCs. They tell us by how many dollars consumption increases if the independent variable increases permanently by one dollar. Note that, since our data are quarterly, the MPCs have to be multiplied by 4 in order to obtain the change in annual consumption.
For the IV fixed-effects estimate we find an MPC for income of 0.57, a stock market wealth effect of 0.021 and a housing wealth effect of 0.007. If we exclude indirect stock market holdings the stock market wealth effect falls to 0.015, although – taking the standard errors into account – the difference is not significant. The coefficient on ‘other wealth’ is significant and it is in the range of the stock market wealth effect, which is consistent with the view that its components, other financial wealth and personal debt, have a significant effect on long-run consumption. All coefficients are statistically significant at the 1 per cent level regardless of whether we use the OLS or the IV estimator. The use of the IV estimator does affect the coefficient on income substantially but the wealth effects are only slightly changed.[21] One noteworthy result is that the housing wealth effect is lower than the stock market wealth effect. For the standard fixed-effects estimators (OLS and IV) we can comfortably reject that the stock market and housing effect are equal at the 1 per cent level of significance.
The panel DOLS estimator, which takes account of both dynamics and endogeneity, finds a long-run stock market wealth effect of 0.023 and a housing wealth effect of 0.008, with both estimates statistically significant. The housing wealth effect is in the range of that estimated by the OLS and IV methodologies. However, the stock market effect is somewhat higher than that from the IV estimator. This is also true for the version with direct equity only, which has a rather high MPC at 0.025 but also a standard error which is twice the size of that obtained with the other estimators. Again, the long-run stock market wealth effect is significantly larger than that of housing wealth.
4.4 The Mean Group Estimator
The results of the SUR estimation are presented in Table 2 and Table 3. Although the SUR yields a consumption function for each state, we are primarily interested in the mean group estimator in Table 2. We report results from both the standard estimation using the Zellner GLS estimator as well as an IV version of this estimator.
| All equity | Direct equity only | ||||
|---|---|---|---|---|---|
| Zellner GLS | IV | Zellner GLS | IV | ||
| Yt | 0.265* (0.036) |
0.376* (0.057) |
0.295* (0.033) |
0.429* (0.048) |
|
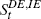 |
0.030* (0.001) |
0.027* (0.002) |
|||
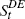 |
0.022* (0.003) |
0.019* (0.003) |
|||
| Ht | 0.008* (0.001) |
0.009* (0.001) |
0.006* (0.001) |
0.007* (0.001) |
|
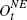 |
0.028* (0.002) |
0.023* (0.002) |
|||
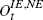 |
0.032* (0.002) |
0.028* (0.002) |
|||
|
Notes: All variables are in real per capita terms and in levels. Constants are not reported. Standard errors are in parentheses and * denotes significance at the 5 per cent level. The mean group estimator reported here is the version which uses an unweighted average of the estimates for each state. The standard error of the mean group estimator is calculated assuming the estimates for each state are independent. |
|||||
| Zellner GLS estimator – all equity | ||||||
|---|---|---|---|---|---|---|
| NSW | VIC | QLD | SA | WA | Mean group estimator | |
| Yt | 0.319* | 0.296* | 0.264* | 0.317* | 0.129 | 0.265* |
| (0.057) | (0.053) | (0.101) | (0.087) | (0.096) | (0.036) | |
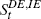 |
0.039* | 0.039* | 0.025* | 0.024* | 0.024* | 0.030* |
| (0.003) | (0.002) | (0.004) | (0.002) | (0.004) | (0.001) | |
| Ht | 0.003* | 0.004* | 0.012* | 0.005 | 0.018* | 0.008* |
| (0.001) | (0.001) | (0.002) | (0.003) | (0.003) | (0.001) | |
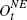 |
0.034* | 0.029* | 0.037* | 0.023* | 0.018* | 0.028* |
| (0.004) | (0.003) | (0.004) | (0.003) | (0.007) | (0.002) | |
| No of obs | 69 | 69 | 69 | 69 | 69 | |
| R2 | 0.98 | 0.99 | 0.97 | 0.97 | 0.96 | |
| IV estimator – all equity | ||||||
| NSW | VIC | QLD | SA | WA | Mean group estimator | |
| Yt | 0.385* | 0.350* | 0.558* | 0.519* | 0.067 | 0.376* |
| (0.066) | (0.081) | (0.184) | (0.132) | (0.134) | (0.057) | |
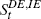 |
0.034* | 0.038* | 0.015* | 0.022* | 0.024* | 0.027* |
| (0.003) | (0.002) | (0.006) | (0.002) | (0.005) | (0.002) | |
| Ht | 0.005* | 0.004* | 0.011* | 0.004 | 0.021* | 0.009* |
| (0.001) | (0.001) | (0.002) | (0.003) | (0.004) | (0.001) | |
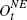 |
0.026* | 0.026* | 0.031* | 0.019* | 0.011 | 0.023* |
| (0.005) | (0.003) | (0.004) | (0.004) | (0.007) | (0.002) | |
| No of obs | 67 | 67 | 67 | 67 | 67 | |
|
Notes: All variables are in real per capita terms and in levels. Constants are not reported. Standard errors are in parentheses and * denotes significance at the 5 per cent level. The mean group estimator reported here uses an unweighted average of the estimates for each state. The standard error of the mean group estimator is calculated assuming the estimates for each state are independent. |
||||||
Looking at the IV mean group estimator, the housing market wealth effect of 0.009 is similar to those of the fixed-effects estimators of 0.007 and 0.008. The mean group estimator puts the stock market wealth effect at 0.027 which is higher than any of the fixed-effects estimators, and with more than 10 cents in the dollar annual MPC also rather implausibly high. Using directly held equity only, the MPC is lower at 0.019. This is somewhat higher than the corresponding coefficient for the fixed-effects estimators. The income effect of 0.4 is lower than those estimated in the fixed-effects models which range from 0.5 to 0.6.
Table 3 reports the details of estimates for the individual states. The stock market wealth effects and the housing wealth effects are positive and – with one exception – significant. Some variation in both the housing wealth effect and the stock market wealth effect is probably not surprising. As there are substantial differences in both types of wealth across states and as housing markets are strongly influenced by regional developments, we gain some extra information that – using state-level data – allows us to disentangle the housing wealth effect from the stock market wealth effect. On the other hand, we may also have more noise in the state-level data leading to variation in the estimates across states. The variation documented in Table 3 is large enough to raise some concerns over the validity of the homogenous slope restriction of the fixed-effects model. We would certainly caution against focusing on the results of the model for any individual state.
Encouragingly, the mean group estimator is in line with the fixed-effects estimators, indicating that this variation washes out when we look at the average effect on the macroeconomy as a whole. Thus we can be reasonably confident about our estimates of the wealth effects at the ‘average’ (i.e. national) level, even if the range of estimates for the particular states seems implausibly wide.
When we compare our results with the long-run wealth effects estimated by other studies a number of differences arise. Converted into annual MPCs, we find that stock market wealth increases consumption by about 6 to 9 cents in the dollar. In comparison, Bertaut (2002) finds a long-run effect of stock market wealth of 5 cents in the dollar while the estimates by Tan and Voss (2003) range from 4 cents in the dollar to 16 cents in the dollar.[22] Our estimate is broadly consistent with the – admittedly wide – range of estimates provided by other studies. It lies above the total wealth effect of 0.04 estimated by Tan and Voss (2003) for Australia. However, this should not be entirely unexpected, as our housing MPC is lower than 0.04. Since housing wealth accounts for a large share of Australian households' assets, this lower MPC is being balanced by an accordingly higher MPC on stock market wealth. The stock market effect lies also at the higher end of those estimated for other countries, but the lower end of our range is well within the range found for other countries.
Our long-run housing wealth effect translates into an annual MPC of around 3 cents in the dollar. This lies at the upper end of the range reported by Tan and Voss (2003), who find an insignificant effect of housing wealth on consumption of between minus 4 cents and plus 4 cents in the dollar. Similar to Case et al (2001), using state-level data we have found both a significant housing market and stock market wealth effect for Australia. But, unlike their study, which finds that the housing effect in the US is larger than the stock market effect, we have confirmed the result from previous studies for Australia which found that the stock market wealth effect is larger than the housing wealth effect.
4.5 Estimation Using Aggregate Data
Our estimation strategy is based on state-level data. This raises the question what do we gain from using state-level data rather than aggregate-level data? As we have chosen a different specification from that of previous studies, a direct comparison may be difficult. We therefore estimate an aggregate consumption function using our model, allowing us to compare our state-level results with an aggregate benchmark[23]. The results for our model using aggregate data are presented in Table 4. Again, the model is estimated in levels and in real per capita terms.
| All equity | Direct equity only | ||||||
|---|---|---|---|---|---|---|---|
| IV | ECM | DOLS | IV | ECM | DOLS | ||
| Yt | 0.713* (0.074) |
0.803* (0.146) |
0.661* (0.061) |
0.645* (0.061) |
0.696* (0.125) |
0.592* (0.052) |
|
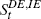 |
0.020* (0.003) |
0.022* (0.005) |
0.024* (0.003) |
||||
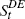 |
0.011* (0.004) |
0.014 (0.008) |
0.015* (0.004) |
||||
| Ht | 0.002 (0.002) |
−0.004 (0.004) |
0.000 (0.002) |
0.002 (0.002) |
−0.002 (0.004) |
0.001 (0.002) |
|
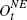 |
0.030* (0.004) |
0.035* (0.006) |
0.035* (0.003) |
||||
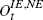 |
0.029* (0.003) |
0.032* (0.005) |
0.033* (0.003) |
||||
| No of obs | 69 | 68 | 68 | 69 | 68 | 68 | |
| R2 adjusted | 0.98 | 0.99 | 0.98 | 0.99 | |||
| SE regression | 45 | 70 | 34 | 41 | 68 | 34 | |
| DW | 1.13 | 2.12 | 0.92 | 1.04 | 2.20 | 0.84 | |
|
Notes: All variables are in real per capita terms and in levels. Only long-run coefficients are reported. Constants are not reported. Standard errors are in parentheses and * denotes significance at the 5 per cent level. For the IV estimations we use the first and second lags of income and contemporaneous values of the other independent variables as instruments. |
|||||||
How do these results compare to the fixed-effects panel? Compared with the state-level results in Table 1, the income effect is higher for the aggregate-level data, ranging from 0.59 to 0.80, which is in line with those found by other studies (e.g., Tan and Voss (2003)). The stock market wealth effect ranges from 0.011 to 0.024 and is close to the panel-data estimate of 0.015 to 0.027. The housing wealth effect, which ranges from −0.004 to 0.002, is substantially smaller than the panel estimates of around 0.008.
One can detect one unifying theme in the results in Table 4: in all models the stock market wealth effect is significant while the housing effect is insignificant. Note that this general theme holds for other aggregate level studies, such as Tan and Voss (2003), as well. This is where the value of state-level data can be seen most clearly. With state-level data we continue to find a significant stock market wealth effect and we find that this effect is at least as large as the housing wealth effect. But with state-level data the housing wealth effect becomes significant, in both the fixed-effects and the mean group estimators. As discussed earlier, this result suggests that the insignificance of the coefficient at the aggregate level is due to multicollinearity, which could be mitigated using state-level information.[24] Of course, like any estimation, our results may be sensitive to the specific assumptions made, such as the time period over which we estimate or the model specification chosen. The next section therefore briefly discusses the robustness of the coefficients through time.
Footnotes
However, there may be differences across states in the share of equity holdings in total wealth so one may still get extra information from state-level data. [13]
Tasmania, ACT and the Northern Territory are excluded due to data limitations. [14]
Of course, this assumption would be a problem if stock owners in different states held equity portfolios which are substantially different in terms of their price movements. We have currently no data to test this assumption on a broad enough level. [15]
Alternative house price series, such as the median dwelling price series by the Real Estate Institute of Australia or the Residex Repeat Sales index, have a lower geographical coverage. In any case, we found that the difference in estimation results due to the choice of house price index is negligible. [16]
We confirmed the non-stationarity using unit root tests on the individual series and panel unit root tests. Cointegration tests suggested that the variables are cointegrated. Of course, this is not surprising as consumption functions are the classic example for cointegration analysis. [17]
For example, Ludvigson and Steindel (1999) for the US and Tan and Voss (2003) for Australia. [18]
The mean group estimator can either be an unweighted average or a weighted average of the coefficients. The weighted average version uses the estimated variance-covariance matrix for the weights. Both estimators are consistent. [19]
We use lags of income and contemporaneous values of the other independent variables as instrument. [20]
The MPC of income is rather low. More generally, other studies have found this coefficient to be unstable. In our case, changes in the time period, the inclusion of dynamics and the inclusion of other variables, such as ‘net other wealth’, affect its size considerably. Other research has suggested that the assumption of a constant real interest rate matters for this coefficient. Due to data limitations and as this coefficient is not the focus of our study, we have not modelled this aspect further. [21]
The specification by Tan and Voss (2003) differs in a number of dimensions from ours. They estimate the effect on non-durable consumption only whereas we use total consumption. As a result, they include durable consumption in their wealth measure. Finally, they estimate their model over a slightly different sample period from ours. [22]
Time series estimation techniques such as an error correction model (ECM) allow us also to judge how long it takes for the long-run effects of a permanent wealth change to pass through to consumption. Although the results regarding the dynamics are sensitive to different specifications, some preliminary analysis suggests that it takes several years for a permanent change in wealth to fully affect consumption, in line with other studies, such as Tan and Voss (2003), who find a time span of around 16 quarters. [23]
Statistical measures suggest also that the degree of multicollinearity is lower for the state-level data set. For example, the condition index (CI) suggested by Belsley, Kuh and Welsch (1980) measures collinearity within a group of variables (a higher CI suggests more multicollinearity). The CI for the aggregate data set is 9.56, the median CI for the individual states is 8.43 and the CI for the pooled state-level data set is 3.94. [24]