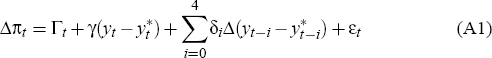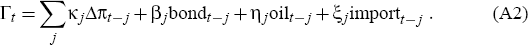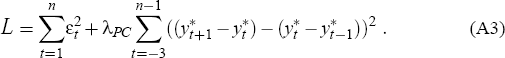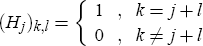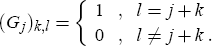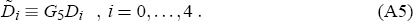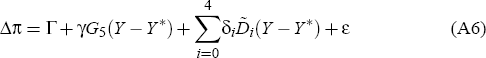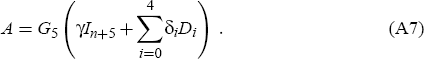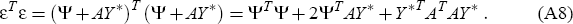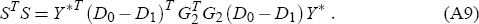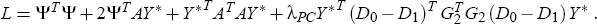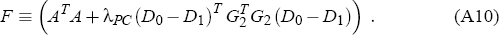RDP 2002-06: Output Gaps in Real Time: are they Reliable Enough to use for Monetary Policy? Appendix A: Implementation of the Phillips Curve Approach

Suppose that, over a sample period t = 1,…,n, we have a model of inflation of the form

where Γ_t is some linear combination of past changes in inflation together with bond market inflation expectations, oil price inflation and import price inflation:

Note that this specification is simply a re-writing of our generic Phillips curve, equation (1).

With such a model, we wish to minimise the loss function

Note that the latter sum in equation (A3) is taken to run from t = −3 because equation (A1) involves 4 lags of ‘change in the output gap’ terms. This equation therefore requires values for potential output over the 5 periods (t = −4, −3, −2, −1 and 0) prior to the start of the sample over which it is estimated. Given this, the usual H-P ‘smoothing penalty’ built into L is here computed over the period t = −3, …, (n−1), rather than simply the period t = 2, …, (n−1).

Overall then we seek values for the (n + 5)×1 vector 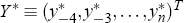and for the parameters {κ_j}, {β_j}, {η_j}, {ξ_j}, {δ_i} and γ which minimise L. Note that L may itself be written in the form

where ε denotes the n × 1 vector ε ≡ (ε₁, ε₂,…, ε_n)^T and S denotes the (n+3)×1 vector .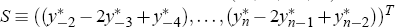

The 4-step iterative procedure we employ for computing these values is as follows.

Step 1: Guess at initial values for the parameter γ and for the parameters {κ_j}, {κ_j}, {β_j}, {η_j}, {ξ_j}, and {δ_i}. To do this we simply use the usual H-P filter to generate a preliminary potential output series, and then, using this series in our model, estimate the corresponding model parameters via ordinary OLS to get initial guesses for these parameters.

Step 2: Using these initial parameter values, solve for the values 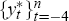via the appropriate analogue (see below) of the usual ‘H-P filter’-type procedure of minimising the loss function L.

Step 3: With these 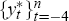re-estimate the inflation equation to get new values for the parameter γ and for the parameters {κ_j}, {β_j}, {η_j}, {ξ_j}, and {δ_i}.

Step 4: Repeat step 2 with these new parameter values, then repeat step 3, and keep doing this until ‘convergence’ is achieved in some suitable sense (that is, until the values of the 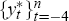and the parameters in the inflation equation stop changing, to within some pre-specified tolerance threshold).

Technical Details of Step 2

It is useful to begin by introducing some notation. For each j = 0, 1, 2,…, let H_j denote the (n + 5) × (n + 5) matrix given by

and let G_j denote the (n + 5 − j) × (n + 5) matrix given by

From these core matrices we may then construct, first of all, the (n + 5) × (n + 5) ‘lagged first differencing’ matrices D₀,D₁,D₂,D₃ and D₄ given by D_i ≡ H_i − H_{i + 1}, i = 0,…, 4. Thence in turn we may form the trimmed n × (n + 5) versions of these matrices, 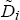, defined by

The importance of these 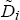matrices derives from the fact that, over the sample period t = 1,…, n, we may now write equation (A1) in vector form as

where Δπ denotes the n × 1 vector (Δπ₁, Δπ₂, …, Δπ_n)^T, Γ the n × 1 vector (Γ₁, Γ₂,…,Γn)^T, and Y the (n + 5) × 1 vector (y₋₄, y₋₃,…,y_n)^T. Re-arranging equation (A6), and using also definition (A5), then yields that ε = Δπ −Γ−A(Y−Y^*), where A denotes the n × (n + 5) matrix

Now define a new n × 1 vector, Ψ, by Ψ ≡ Δπ − Γ − AY. Then ε may now be written in the form ε = Ψ + AY^*, where Ψ is independent of potential output. We then obtain the following formula for the first of the two terms on the right-hand side of formula (A4) for L:

Turning to the second of the two terms on the right hand side of formula (A4) for L, observe that we may write S = G₂ (D₀ − D₁)Y^*, whence also we have that

Combining equations (A4), (A8) and (A9) we therefore derive that

The first order conditions for minimising L then yield that FY^* = −A^TΨ, where F denotes the (n + 5)×(n + 5) matrix

Therefore, the unique solution for the potential output vector Y^* which minimises L, for the given values of the parameters γ, {κ_j}, {β_j}, {η_j}, {ξ_j} and {δ_i}, is simply

where F, A and Ψ are as defined above.