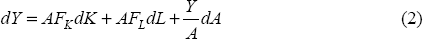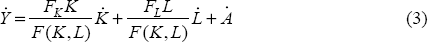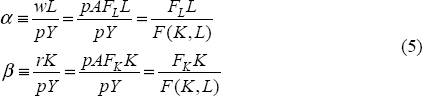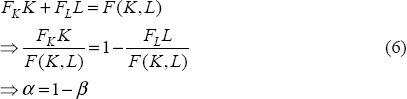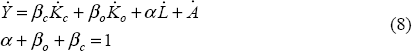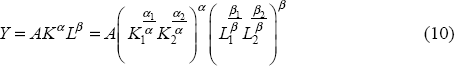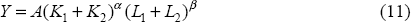RDP 2002-02: Australian Use of Information Technology and its Contribution to Growth 3. The Theory

3.1 Growth Accounting

The method used to identify the effects of capital, labour and productivity on growth was introduced by Bob Solow in 1957 (Solow 1957). The underlying principle is quite simple and best understood with reference to a Cobb-Douglas production function. Nonetheless, the derivation below does not rely on any feature of this production function other than it being homogenous of degree one, that is, it displays constant returns to scale.

Suppose output is produced according to Equation (1):

where A denotes the level of productivity and K and L are factor inputs of capital and labour. Output growth can be decomposed by taking a total derivative of Equation (1):

Rearranging gives:

where dots over a variable denote the proportionate change, i.e., 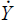= dY/Y.

Profit maximisation allows us to make some further simplifications. The first order conditions from a firm's profit maximisation problem are:

where r is the rental rate of capital (which includes depreciation) and w is the wage rate.

Manipulating these expressions we get:

Further, assuming that the function exhibits constant returns to scale, we know that:

Thus, we can write the decomposition as:

where α is the labour share of income as given in Equation (5). Given measures of capital stock growth, labour input growth, labour's share of factor income and output growth, productivity growth is derived as a residual.

If more than two factors are considered it is a simple matter to expand the production function to include other inputs and the resulting formula is practically identical. In particular, capital can be broken into computer capital and other capital. This leads to a decomposition of the form:

where K_c represents computer capital and K_o represents other capital.

3.2 Aggregation Issues

As we are using industry-level data the aggregation method is relevant.^[4] Suppose, for now, that the economy can be divided into two industries, 1 and 2, and that the only inputs to production in each sector are capital and labour. Three broad ways of aggregating the data can be considered:

In the first, economy-wide output is the sum of output produced in each industry. Here, the output produced in each industry is a function of capital, labour and the level of technology in that industry. We will use this method in this paper. The second can be thought of as a standard economy-wide Cobb-Douglas function where the capital and labour inputs are an index based upon individual industry capital stocks and employment. This method assumes that capital and labour are complementary across industries as well as industry output.^[5] In the last there is still an economy-wide production function but the aggregation of capital and labour is different. In this case, capital and labour inputs are summed across industries. This functional form assumes that capital and labour are substitutable across industries. However, this assumption is not normally used when industry-level data are available. Implicit in this functional form is the assumption that there is no difference between capital or labour across sectors; this does not seem highly likely. Nonetheless, because they lack industry-level data, Oliner and Sichel (2000) implicitly use this method. Finally, one could combine the aggregation methods in Equations (10) and (11) to produce a production function like:

This is, fundamentally, the specification the ABS uses when it publishes its estimate of productivity growth in the national accounts.^[6]

As each aggregation method makes different assumptions regarding the way the economy is ‘structured’, slightly different measures of output, capital and labour indices, and productivity will result. While none is perfect, we choose to use the method in Equation (9) due to larger problems with the other approaches. An additional reason for choosing this approach is because it means that industry-level results and aggregate results are consistent. To generate industry-level results one must use industry-level production functions like those in Equation (9). Changing to a function like Equation (10) or (11) to generate aggregate results would then involve a fundamental change in assumptions. Thus, aggregate MFP calculated using Equations (10), (11) or (12) would bear no particular relation to industry-level MFP.

The problem with the capital indices in Equations (10) and (12) is that changes in the distribution of capital, or productive units (including both capital and labour), across sectors can induce changes in the index even if there is no change in the aggregate amount of capital in the economy.^[7] It is also possible for the capital stock to grow in every industry but for the index to decline.^[8] We find this feature undesirable and, thus, choose an alternative method of aggregation. Equation (11), on the other hand, makes no distinction between industries or about the distribution of inputs across industries. Thus, output is unaffected if all the labour is concentrated in one industry or spread evenly across all industries regardless of the distribution of capital. However, as mentioned above, this equation is only given to show the implicit aggregation method used when industry-level data are unavailable. Finally, since Equation (12) inherits problems from both of the other methods we also choose to avoid it. Nonetheless, to provide an estimate of the effect our choice has on the aggregate results we present results from using the alternative formulations in Section 5.2.

3.3 Alternative Assumptions

While it has been standard in the literature to assume constant returns to scale and profit maximisation, it is conceivable that these assumptions may not hold. Since Hall (1988) demonstrated that macroeconomic data in the US are inconsistent with the joint hypothesis of constant returns to scale and marginal cost pricing, the assumption of constant returns to scale has been under pressure. Unfortunately, attempts to quantify the degree of departure from constant returns to scale and reconcile this with observations about industry structure have been unsatisfactory. For example, if industries exhibit increasing returns to scale, theory would suggest that they would tend towards monopolisation; however, very few industries are, in fact, monopolised. Investigating the returns to scale of Australian industries would be a worthwhile project but is beyond the scope of this paper. We proceed by making the standard assumption of constant returns to scale while acknowledging that our findings would need to be revised if significant departures from constant returns to scale for Australian industries are demonstrated in the future.

Strictly interpreted, the assumption of profit maximisation in this work implies that firms adjust their inputs to profit maximising levels every year. If adjustment takes longer than a year, because there are costs to adjustment or new technologies take some time to be adopted, this will not be true. In particular, firms may have levels of computer capital that are below the profit maximising level in certain years due to limits on their speed of adjustment. In this case the marginal value product of computer capital will exceed its price. This could lead to a systematic overstatement of MFP growth and understatement of the contribution of computer capital to growth. This phenomenon is part of a broader problem with the measurement of computer productivity and embodied technical change. Specifically, if the quantity of computer capital is understated due to problems in estimating the degree of embodied technical change (i.e., comparing the output from this year's 2GHz Pentium 4 with last year's 1GHz Pentium III) a similar understatement of computer capital's contribution to growth and overstatement of MFP growth will result.^[9] It is difficult to assess the extent of this problem. To address this issue we consider whether there is any consistent correlation between computer use and MFP growth across industries in Section 6.2. As argued above, problems with measurement or adjustment costs should show up in a correlation between computer use and MFP growth. The results from Section 6.2, that there is no discernable correlation, suggest that this problem may not be a significant source of error in our calculations. However, the difficulties involved in the whole exercise mean that the problem may just be well disguised – we are far from dogmatic about this point. Nonetheless, the results in Section 6.2 suggest there is no prima facie case for systematic errors distorting the MFP growth and computer contribution numbers.

Footnotes

Even though we use a Cobb-Douglas production function to illustrate the various methods of aggregation, the approach we use does not require this assumption – the only condition we require is constant returns to scale. Nonetheless, Carmichael and Dews (1987) find that the Cobb-Douglas functional form is a reasonable first approximation for an empirical economy-wide production function for Australia. [4]

Equation (10) could be rearranged to look like Y = AY₂Y₁ where 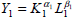. The complementary nature of industry output is clearer in this case. [5]

The estimates referred to are the experimental productivity measures published in the Annual National Accounts, ABS Cat No 5204.0. These can be found in Table 20 of the 2000–01 National Accounts. [6]

The following numerical example may help to illustrate the point. Suppose that there are five units of capital, four in Industry 1 and one in Industry 2. Also, suppose that there is no labour involved in the production process and that the coefficients reflect income shares – an assumption that comes directly from assuming that firms maximise profit. By moving one unit of capital from Industry 1 to Industry 2 the capital index and output would be decreased since 4^4/51^1/5 > 3^3/52^2/5. This seems an undesirable property. [7]

The following numbers may help to illustrate this point: 20^20/211^1/21 > 21^21/232^2/23. The assumptions are the same as in the previous footnote. [8]

Of course, computer capital could be overstated but understatement seems the more likely problem. [9]