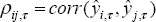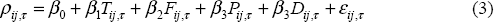RDP 2001-05: Understanding OECD Output Correlations 2. Framework

Our objective is to try to explain why output growth rates of some pairs of countries are highly (positively) correlated and why others are not. This is a complicated task and economic theory does not provide a great deal of guidance, apart from suggesting particular directions to explore. Consequently, we proceed in a relatively ad hoc manner, using a series of simple regression models to better understand what underlies the cross-section variation in the bilateral output growth correlations among the OECD countries in our sample.

We do, however, attempt to put some structure on our approach. As noted in the introduction, there are two potential explanations for the correlation of output growth that we observe. The first explanation is that country or region specific shocks are transmitted through various economic interdependencies between countries. That is, it is economic transmission channels that are important for the synchronisation of business cycles among the industrialised economies and that the stronger the transmission channels between two countries the larger the expected (positive) correlation between their growth rates. The second explanation is that there are common shocks affecting the industrialised economies. In this case, we expect that countries with similar economic structure are likely to be highly correlated. Our approach is to build upwards to an empirical model that captures the contributions of both these types of explanations.

We consider three broad types of transmission channels in the analysis that follows; trade in goods and services, trade in financial assets, and the coordination or similarity of monetary policies. This list is not exhaustive, for example it does not consider the transmission of confidence or sentiment nor does it consider the coordination of fiscal policies; however, it does capture what are likely to be the three most important channels.

To examine the role of common shocks, we consider a number of economic, institutional and geographic characteristics. In particular, we examine the similarity between countries of industry structure, corporate governance, structural economic policies, adoption of new technologies, as well as whether countries share a common language or are geographically adjacent. Some care, however, must be taken when interpreting these results. In some instances, it will be natural to interpret these as suggesting a similar response to common shocks; for example, the similarity or otherwise of industry structure. In other instances, however, similarity in certain characteristics may suggest a greater likelihood of integration of the two economies; for example, a shared language. We return to this issue when we discuss the empirical results.

2.1 Regression Model

Our empirical model is a cross section regression model using the bilateral correlation pairs as the dependent variable. The sample period over which the correlations are measured is denoted τ. There are N countries in the sample. For country i, the four-quarter-ended growth rate of GDP over the sample period τ is 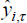denoted . The correlations are denoted,

for all i, j ∈ N, i ≠ j.^[7] Our objective is to explain these bilateral correlations, either as a function of economic interaction between any two countries or, in the case of common shocks affecting all economies, as a function of common economic structure.

It is useful to begin by focusing initially on bilateral trade intensity, i.e. some measure of the importance of bilateral trade in goods and services between two countries. Denote the trade intensity between two countries i and j as T_ij.^[8] Then the regression model is:

The error term ε_ij,τ is assumed to be independently and identically distributed with mean zero.

There is, however, a difficulty with estimating the above model using ordinary least squares, as noted in Frankel and Rose (1998), which uses this model to consider empirical issues of optimum currency areas. These authors note that two countries that have a large amount of bilateral trade are more likely to link their currencies together (either explicitly or implicitly). This implies that the same two countries will operate monetary policy (and possibly other policies) in a similar fashion and this may, as a consequence, synchronise the business cycles of these two countries. In this case, it is not only the trade of goods and services that cause the business cycles to be correlated but rather the operation of economic policies. What this means for the regression above is that using ordinary least squares will give the wrong answer; it cannot identify the separate contribution from trade and the contribution from the common policies enacted because of the close trading relationship.

The difficulty that Frankel and Rose highlight is part of a more general problem; economic characteristics and/or interdependence between two economies are likely to explain bilateral trade as well as bilateral GDP correlations. One approach to resolve this problem is to specify a simultaneous equation structural model that explains both the correlations of GDP growth and bilateral trade interdependencies as well as the other interdependencies of interest. This is beyond the scope of this paper. Instead, we use instrumental variables.

To provide some intuition, we can go a little ways to constructing a structural model. In particular, we could make use of the gravity model (Rose 2,000) for bilateral trade:

Here Z_ij,τ is a set of exogenous variables such as the geographic distance between the two economies and whether or not the two economies are adjacent. Variables such as these have been shown to explain bilateral trade very well and can be reasonably treated as exogenous. Estimation of Equation (1) by instrumental variables can be viewed as first estimating Equation (2) and then using the predicted values from this regression in place of those in Equation (1) (that is, two stage least squares). What we are doing is first predicting how much trade two countries should have based upon their exogenous characteristics. We then use this predicted trade intensity to explain the bilateral correlation. The fact that we are using predicted trade rather than actual trade means that we will not fit the data as well; but it also means that we can get an estimate of β₁ that only depends upon trade (more correctly, things that explain trade), and not policy or other forms of interdependence. Of course, this assumes that the variables we are using to predict trade do not also help explain, directly or indirectly, the bilateral correlations.^[9]

Ideally, we would like to augment Equation (1) with other channels for the transmission of shocks. We would also like to control for the possibility that what underlies the co-movement of two economies is not the transmission of shocks from one country to another but rather a common shock to both economies from an external source. In this case, it is necessary to consider what characteristics two countries have in common that ensure they move together in response to the common shock (e.g. an oil price shock). A more general regression model is then:

For any two countries i and j, F_ij,τ measures the degree of financial integration; P_ij,τ the degree of policy interdependence, and D_ij,τ a measure of the similarity (or dissimilarity) of the economic structure of the two economies. More generally, D_ij,τ can be a set of variables describing common characteristics that either explain a common response to common shocks or explain business cycle correlations directly.

It is worth highlighting now the difficulties associated with estimating Equation (3). Broadly speaking, the data we have is not rich enough to adequately identify the contributions of each of these different channels or characteristics. Put differently, if we estimate an equation such as (3) it is very difficult to get sensible results. If we viewed the problem in a standard ordinary least squares (OLS) regression context, there is a great deal of co-linearity between the variables of our general model. As a consequence, we proceed from the simple to the more complex in an attempt to tease as much information from the data as we can.

Footnotes

There are N(N-1)/2 such correlations. [7]

In the following section we discuss in detail our choice of variables and how they are measured. [8]

The above is an attempt to describe the instrumental variable methods we employ using a two stage least squares interpretation of the estimation. [9]