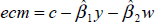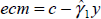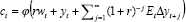RDP 2000-09: Consumption and Wealth 3. Empirical Results
December 2000
- Download the Paper 337KB
3.1 Data
The series used for estimation are household consumption expenditure on non-durable goods, household after-tax labour income, household net wealth and its components, non-financial and financial net wealth.[8] Non-durable consumption expenditure excludes clothing, footwear, furnishings and vehicles.[9] To calculate component wealth measures net of household debt, we subtract off a proportion of household debt, based on the relative weight of each type of asset, from each measure of asset wealth.[10] All series are quarterly, seasonally adjusted, and measured in real per capita terms, in levels not logs. The implicit price deflator for non-durable consumption is used to express all variables in real terms (constant 1997/98 dollars).
The full sample considered is 1980:Q1–1999:Q3; the principal series over this sample are presented in Figures 3 and 4. We also consider two sub-samples, 1980:Q1–1988:Q3 and 1988:Q4–1999:Q3. We divide the sample at this point for a number of reasons. First, 1988:Q4 is the first quarter for which there is quarterly data for household financial wealth provided by the ABS; prior to this, we have annual estimates that must be interpolated. Second, as previously discussed, the household net wealth data undergoes a substantial persistent rise in the late 1980s. This behaviour makes net wealth quite difficult to model over the whole sample.[11] In addition, there are reasonable grounds for treating this as a type of structural break. Inspection of Figures 3 and 4 suggests that consumption was little affected by the very large increase in wealth of the late 1980s; certainly, there is no discernible change in the long-run behaviour of consumption. This suggests that the late 1980s increase in household net wealth might be best regarded as an unusual event. By splitting the sample where we do, we mitigate the effect this episode has on the estimation.[12]
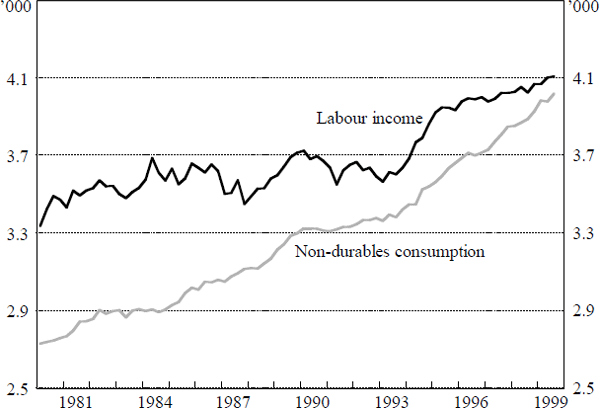
In addition to the dramatic changes in net wealth over the sample, Figure 4 provides evidence of further difficulties for estimation. Notably, the relationship between consumption and labour income appears to differ substantially over the two periods. In the 1980s, consumption grows more quickly than labour income while in the 1990s, consumption and labour income share a similar, and higher, growth rate. While it is possible that this may be part of a complicated linear relationship with net wealth that is consistent with permanent income/life cycle theory, empirically this does not appear to be the case, as we demonstrate below.
Furthermore, there is a reasonable structural interpretation to this changing relationship. During the 1980s, Australia underwent considerable deregulation of its financial markets providing households with a greater ability to access credit markets. This might explain the rapid growth of consumption relative to labour income in the 1980s and the seemingly stable near one-to-one correspondence of the 1990s.[13]
The estimation has two parts. The first involves the models in Equations (1) and (2); we refer to these as steady-state models. We then estimate Equations (3) and (4) conditional on the steady-state estimates.[14] An alternative would be to model the dynamics and steady-state relationships jointly, either in a single equation or systems framework. We find this two-stage approach to be the most practical, especially for identifying and dealing with instability in the steady-state relationships.
3.2 Steady-state relationships
Estimation of empirical models based upon Equation (1) or (2) must address two standard problems. First, the series involved are generally assumed to be first difference stationary and empirically this is likely to be a reasonable assumption.[15] Standard ADF tests cannot reject a unit root null hypothesis for any of the variables over any of the samples. These sorts of tests, however, may not have much power in the small sub-samples and in the presence of structural breaks, which we suspect characterises the full sample of data, so we do not examine this issue in any great detail. For both the full sample and the sub-samples, we assume that the series can be reasonably represented as first difference stationary series and proceed.
Under this assumption, the steady-state conditions can be interpreted empirically as cointegrating relationships. To estimate these relationships, we use the single equation modified DOLS/DGLS procedure suggested by Stock and Watson (1993). In the first instance, we use the dynamic OLS estimates with Newey and West (1987) standard errors to correct for any residual serial correlation.[16] Based upon these estimates, we then test whether the residuals of the cointegrating vector are stationary, providing evidence in favour of cointegration. Where we do find evidence of cointegration, we then re-estimate the relationship using dynamic GLS (generalised least squares) estimation assuming an AR(1) process for the residuals.[17] Although the two methods are asymptotically equivalent, for the small samples here it seems preferable (if possible) to model the residual serial correlation explicitly rather than rely on the asymptotic Newey-West correction.
Table 2 presents estimates of Equations (1) and (2) over the full sample and two sub-samples.[18] For Equation (1), we present two models, one using aggregate net wealth and the other using a decomposition of net wealth, non-financial and financial net wealth, denoted wNF and wF. For each model, the DOLS estimates of the cointegrating or steady-state vector are presented (the constant is omitted). Also reported is an Augmented Dickey-Fuller t-test for the residuals of each cointegrating vector. For the two variations of Equation (1), only for the second sub-sample do we reject the null hypothesis of a unit root in the residuals at standard significance levels; that is, only for these models do we have evidence of cointegration. For the other samples, we find no evidence of cointegration.
| 1980:Q1–1988:Q3 | 1988:Q4–1999:Q3 | 1980:Q1–1999:Q3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| β1 | β2 | β1 | β2 | β1 | β2 | ||||||
| c−β1y−β2w | |||||||||||
| DOLS | 0.4180 | 0.0264 | 0.6780 | 0.0089 | 0.3974 | 0.0180 | |||||
| (0.3016) | (0.0055) | (0.1096) | (0.0015) | (0.1110) | (0.0014) | ||||||
| DGLS(AR(1)) | 0.6022 | 0.0102 | |||||||||
| (0.1350) | (0.0023) | ||||||||||
| ADF(2) | −2.2075 | −3.1925* | −2.4282 | ||||||||
| β1 | β2 | β3 | β1 | β2 | β3 | β1 | β2 | β3 | |||
| c−β1y−β2wNF | |||||||||||
| DOLS | −0.1588 | −0.0132 | 0.0483 | 0.5887 | −0.0097 | 0.0417 | 0.3478 | 0.0021 | 0.0405 | ||
| (0.1229) | (0.0164) | (0.0153) | (0.0941) | (0.0081) | (0.0133) | (0.0914) | (0.0032) | (0.0036) | |||
| DGLS(AR(1)) | 0.5726 | 0.0102 | 0.0107 | ||||||||
| (0.1678) | (0.0100) | (0.0153) | |||||||||
| ADF(2) | −2.7059** | −2.0186 | |||||||||
| γ1 | γ1 | γ1 | |||||||||
| c−γ1y | |||||||||||
| DOLS | 0.8890 | 1.2319 | 1.7387 | ||||||||
| (0.4612) | (0.0870) | (0.0916) | |||||||||
| ADF(2) | 0.4655 | −1.8243 | −1.9618 | ||||||||
|
Notes: Estimates are based upon Stock and Watson (1993); regressions include leads and lags of order two. Standard errors are in parentheses. For the DOLS estimates, these are Newey-West (1987) standard errors with lag truncation parameter of two. ADF(2) are augmented Dickey-Fuller t-statistics for the unit root null hypothesis for the residuals of the cointegrating vector. The symbols * and ** denote significance at the five per cent and ten per cent level (based on tables in Hamilton (1994)). |
|||||||||||
The evidence against a steady-state relationship over the full sample suggests that we should focus our attention on the second sub-sample, for which we do find favourable results (at least for the models including wealth measures). There is a further reason, as well. Inspection of the parameter estimates across the samples clearly indicates a great deal of instability in the relationship between these variables. The full sample estimates clearly do not provide a consistent summary of the two sub-samples; moreover, these estimates are clearly at odds with theory and common sense. The coefficient on labour income is improbably low and almost certainly arises because of structural change in the underlying relationships.
For the second sub-sample, where we do have evidence of a steady-state relationship between consumption, labour income and wealth, we can attempt to improve the estimation by modelling any residual serial correlation using the GLS procedure. For the aggregate wealth model, the difference between these and the DOLS estimates is small. For the model with wealth components, however, the estimates differ in an important way. For the DOLS estimates, the coefficient on net non-financial wealth is insignificant while that on net financial wealth is significant and quite large. In contrast, the DGLS estimates for these two coefficients are similar in size but insignificant. These two sets of estimates have very different implications for the relationship between consumption and wealth and it is important to discriminate between them. Previously, we identified the DGLS estimates as preferable on technical grounds (it explicitly models the residual serial correlation). A further reason for accepting the DGLS results is that the coefficient estimates are consistent with the aggregate wealth model. Indeed, it is hard not to conclude that the insignificance arises from a co-linearity problem and that the aggregate model correctly imposes the restriction that the two assets have the same long-run coefficient. This has the additional attractive feature of providing a steady-state relationship that is consistent with consumption theory.
The aggregate wealth model accords reasonably well with expectations. The coefficients are all statistically significant and have values that are consistent with economic theory. The coefficient on net wealth for the DGLS model is 0.01. Recall that this can be compared to a quarterly after-tax real rate of return on assets (assuming that consumption is equal to permanent income). In annual terms, this return converts to approximately 4 per cent, which is certainly of the right order of magnitude.[19] Compared to other studies, however, this estimate is somewhat low. For their study of the US, Ludvigson and Steindel (1999) find a coefficient on aggregate wealth of 0.02, nearly twice what we estimate here. Our estimate is also lower than reported in Macklem's (1994) study for Canada (although a direct comparison to this study is difficult because of differences in the estimated models). Turning to the coefficient on labour income, this is somewhat lower than expectations, given the discussion of the theoretical models, but not entirely unreasonable. Nor in this case is it unprecedented. Both Ludvigson and Steindel (1999) and Macklem (1994) find similar estimates for this parameter.
Evidence of a stationary steady-state condition for consumption, labour income and net wealth in the second sub-sample can be viewed as limited support in favour of the permanent income or life cycle hypothesis for this period, albeit with coefficient estimates somewhat different from the standard simple case under which the coefficient on labour income is equal to one. Further, the fact that no such relationship can be found in the earlier part of the sample suggests that the deregulation of financial markets through the 1980s may have been in part responsible for aggregate consumption now being closer in line with the predictions of these models. This is consistent with arguments presented in Olekalns (1997), although we show in the following section that more exacting tests of the permanent income or life cycle model do not provide support for either of these theories.
Also reported in Table 2 are estimates of Equation (2), the steady-state condition involving consumption and labour income. In this case, we find no evidence of cointegration for any of the samples. This result, which contradicts the predictions of the life cycle model, is consistent with Gali's (1990) results for the US. Gali suggests that likely factors underlying his results are measurement errors associated with the construction of labour income series, persistent fluctuations in financial values and liquidity constraints; all of these are also potential explanations for the failure of the model using Australian data. In particular, the shifting coefficient on labour income over a period that saw substantial deregulation of financial markets as well as periods of very strong growth in asset values suggests that the last two explanations may be particularly important. A possible direction for future research is to determine which, if any, of these factors can explain the rejection of the life cycle model.
3.3 Consumption models
Tables 3 and 4 present estimates for four error correction models of consumption for the sample 1988:Q4–1999:Q3 based upon the steady-state relationships of Table 2. Table 3 uses the steady-state relationship for aggregate net wealth (the DGLS estimate). Table 4 uses the estimates for the steady-state relationship between consumption and labour income, consistent with the life cycle model. Although there is some evidence that this is not a stationary steady-state condition, the coefficient estimates are reasonably consistent with theory and it seems worthwhile to consider the predictions of the life cycle model in further detail.
| (1) | (2) | (3) | (4) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Constant | 0.0466 | (0.0213) | 0.0545 | (0.0158) | 0.0384 | (0.0226) | 0.0502 | (0.0182) | |
| ecmt−1 | −0.0969 | (0.0564) | −0.1179 | (0.0432) | −0.0797 | (0.0716) | −0.1095 | (0.0531) | |
| Δct−1 | −0.2757 | (0.1861) | −0.2324 | (0.1518) | −0.1559 | (0.1718) | |||
| Δct−2 | 0.1140 | (0.1652) | 0.1482 | (0.1759) | |||||
| Δyt | 0.0612 | (0.1721) | −0.0000 | (0.1068) | |||||
| Δyt−1 | 0.1618 | (0.0888) | 0.1572 | (0.0911) | 0.1411 | (0.1166) | 0.1515 | (0.1053) | |
| Δyt−2 | 0.1077 | (0.0798) | 0.0612 | (0.0970) | |||||
| Δwt | 0.0078 | (0.0028) | 0.0081 | (0.0020) | |||||
| Δwt−1 | 0.0026 | (0.0012) | 0.0027 | (0.0011) | |||||
| Δwt−2 | −0.0031 | (0.0027) | |||||||
| ΔwNF,t | −0.0006 | (0.0037) | |||||||
| ΔwNF,t−1 | −0.0004 | (0.0023) | |||||||
| ΔwNF,t−2 | 0.0024 | (0.0033) | |||||||
| ΔwF,t | 0.0095 | (0.0063) | 0.0109 | (0.0054) | |||||
| ΔwF,t−1 | 0.0108 | (0.0046) | 0.0080 | (0.0029) | |||||
| ΔwF,t−2 | −0.0023 | (0.0056) | |||||||
| χ2(l – k) | 0.0263 | 0.2473 | 0.3437 | 0.7983 | |||||
| SSC(Δyt) | 0.5087 | – | 0.5329 | – | |||||
| SSC(Δwt) | 0.6382 | 0.1132 | |||||||
| SSC(ΔwNF,t) | 0.6157 | – | |||||||
| SSC(ΔwF,t) | 0.5429 | 0.4521 | |||||||
| σ | 0.0154 | 0.0167 | 0.0160 | 0.0171 | |||||
|
Notes: The sample is 1988:Q4–1999:Q3. All regressions are estimated using instrumental variables. The instruments are three lags of first differences of US GDP, US net wealth and, for (3) and (4), the S&P500 index. Standard errors, in parentheses, are robust to heteroskedasticity and autocorrelation (the lag truncation parameter is two). Numbers reported for χ2 (l – k) are p-values for the test of over-identifying restrictions; l is the number of instruments and k is the number of variables in the model (Davidson and Mackinnon, 1993, p 236). SSC(x) are measures of instrument quality due to Shea (1997). |
|||||||||
| (5) | (6) | (7) | (8) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Constant | −0.0645 | (0.0620) | −0.0601 | (0.0452) | −0.0504 | (0.0593) | −0.0514 | (0.0465) | |
| ecmt−1 | −0.0658 | (0.0543) | −0.0625 | (0.0401) | −0.0523 | (0.0505) | −0.0541 | (0.0399) | |
| Δct−1 | −0.3184 | (0.1876) | −0.3050 | (0.1549) | −0.2275 | (0.1658) | |||
| Δct−2 | 0.0755 | (0.1522) | 0.1035 | (0.1461) | |||||
| Δyt | 0.0973 | (0.1966) | 0.0569 | (0.1186) | |||||
| Δyt−1 | 0.1645 | (0.0946) | 0.1596 | (0.0842) | 0.1542 | (0.1161) | 0.1644 | (0.1078) | |
| Δyt−2 | 0.1040 | (0.0792) | 0.1059 | (0.0715) | 0.0749 | (0.0886) | |||
| Δwt | 0.0076 | (0.0023) | 0.0068 | (0.0017) | |||||
| Δwt−1 | 0.0033 | (0.0013) | 0.0037 | (0.0013) | |||||
| Δwt−2 | −0.0025 | (0.0023) | |||||||
| ΔwNF,t | 0.0018 | (0.0040) | |||||||
| ΔwNF,t−1 | 0.0010 | (0.0018) | |||||||
| ΔwNF,t−2 | 0.0014 | (0.0031) | |||||||
| ΔwF,t | 0.0089 | (0.0054) | 0.0084 | (0.0055) | |||||
| ΔwF,t−1 | 0.0093 | (0.0048) | 0.0086 | (0.0035) | |||||
| ΔwF,t−2 | −0.0027 | (0.0057) | |||||||
| χ2(l – k) | 0.2281 | 0.4433 | 0.5829 | 0.8493 | |||||
| SSC(Δyt) | 0.5098 | – | 0.5391 | ||||||
| SSC(Δwt) | 0.6300 | 0.0970 | |||||||
| SSC(ΔwNF,t) | 0.6151 | ||||||||
| SSC(ΔwF,t) | 0.5805 | 0.4552 | |||||||
| σ | 0.0155 | 0.0159 | 0.0155 | 0.0173 | |||||
|
Note: See Table 3. |
|||||||||
In all cases, we begin with a general structure allowing lagged differences of consumption, labour income and either net wealth or its components to enter the model. We also include contemporaneous differenced labour income and net wealth variables. As these are possibly endogenous variables, we use instrumental variables for estimation. Where we use aggregate net wealth, the instruments used are three lags of first differences of US GDP and US net wealth. Where we use the components of net wealth, the instrument set also includes the US stock market index, the S&P500 Index.[20] We use a Newey-West (1987) autocorrelation and heteroskedasticity robust covariance matrix estimator.[21] The relatively small sample that we have limits our ability to model the dynamics, so this corrects for any serial correlation remaining in the errors. Further, the time aggregation issues of Campbell and Mankiw (1990) suggest that the errors may have a moving average process. The general models are presented in Tables 3 and 4, as are more parsimonious models based upon eliminating statistically insignificant variables. We retain the error correction term in all models, even though in the general specifications of Table 4 these are at best weakly significant.
Our first concern is the quality and validity of the instruments we use. For each model, a test of over-identifying restrictions is reported. This is a general test for specification and instrument validity (Davidson and Mackinnon 1993, p 235). With the exception of model (1), we cannot reject the restrictions, providing some evidence that for these models the instruments used are valid. For model (1), either the model is mis-specified or the instruments are invalid. Although it is not possible to identify the source of rejection, a comparison with model (3) suggests that mis-specification may be the principal problem. The coefficients on the wealth components in model (3) are not consistent with aggregating these components as is done in model (1). We return to this issue below.
In light of recent work that indicates IV estimates can be quite biased when the instruments are poor (that is, when instruments have low correlation with endogenous regressors), we report a partial R2 statistic (sample squared correlation) due to Shea (1997). This provides a measure of instrument quality in models with multiple endogenous variables and instruments. This statistic can range between zero and one with a very low statistic indicating that the instrument set is poor for a particular endogenous variable (see Shea (1997) for detail). For each regression, there is one such statistic for each endogenous variable x, identified as SSC(x). These numbers are all quite large, with the exception of aggregate wealth in models (2) and (6), suggesting that the instruments are generally quite good.
Prior to examining the parsimonious models, it is instructive to consider the information in the general specifications. Three results emerge consistently across the specifications. First, contemporaneous labour income is not significant in any of the models. This does not appear to be an instrument quality problem; for the general models, the quality of instruments for the labour income variable is always quite high. Second, for both the models of Tables 3 and 4, the coefficients on the two components of net wealth are very different, suggesting that it is not correct to aggregate the two components. Finally, the coefficients on the net non-financial wealth variables are all statistically insignificant. In contrast, net financial wealth is a significant explanatory variable for consumption change.
The parsimonious or restricted models presented in Tables 3 and 4 also share some common features. In all cases, the error correction term is significant at the ten per cent level or smaller. Not surprisingly, the coefficient on the error correction term involving just consumption and labour income is considerably smaller than for the more general error correction term involving net wealth. The former error correction term is very persistent (recall the ADF tests of Table 2), so that empirically we anticipate a slow response to deviations from this steady state. The other common feature is the significance and magnitude of the coefficients on net financial wealth. Moreover, these coefficients are little changed from the general specifications. The consistency of these parameter estimates suggests that they are reasonably robust.
As a further check on the robustness of our results, we re-estimated the models of Tables 3 and 4 in an unrestricted error correction form, as advocated by Banerjee et al (1993). (These results are not reported but are available upon request.) While some aspects of the models are unchanged, there are some important differences. Most notably, the long-run coefficient on labour income has a value close to one while that on net wealth is somewhat smaller than the estimates of Table 2. While these estimates, particularly that on labour income, may seem preferable as they more closely accord with theory and expectations, the residuals of the implied steady-state condition are not stationary for our sample. Asymptotically, the two different estimation methods should provide similar answers; that they do not appears to be a small sample problem. Because the estimates of Table 2 provide us with stationary steady-states conditions we proceed with these estimates.
For the consumption models of Table 3, there are at least two further directions to consider. First, we are modelling non-durables consumption so a natural determinant is the price of non-durable relative to durable consumption goods. Second, it is possible that consumption may depend upon the real interest rate, as the intertemporal relative price of consumption, as theory would predict (Hall 1988). To explore these concerns, we augment model (3) of Table 3 with these variables in turn (the paucity of degrees of freedom precludes a more general approach). These results are reported in Table 5.
| (9) | (10) | (11) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Constant | 0.0409 | (0.0274) | 0.2696 | (0.1158) | 0.1724 | (0.0541) | |||
| ecmt−1 | −0.0869 | (0.0810) | −0.5715 | (0.2489) | −0.3757 | (0.1140) | |||
| Δct−1 | −0.1729 | (0.2155) | 0.2462 | (0.1984) | |||||
| Δct−2 | 0.1758 | (0.2840) | 0.3513 | (0.2262) | 0.3779 | (0.1128) | |||
| Δyt | 0.0147 | (0.2444) | 0.0973 | (0.2520) | |||||
| Δyt−1 | 0.1423 | (0.1398) | 0.0348 | (0.1139) | |||||
| Δyt−2 | 0.0598 | (0.1206) | 0.0264 | (0.1031) | |||||
| ΔwNF,t | −0.0001 | (0.0044) | −0.0021 | (0.0048) | |||||
| ΔwNF,t−1 | 0.0001 | (0.0031) | −0.0068 | (0.0031) | −0.0030 | (0.0016) | |||
| ΔwNF,t−2 | 0.0014 | (0.0041) | 0.0002 | (0.0050) | |||||
| ΔwF,t | 0.0095 | (0.0070) | 0.0102 | (0.0073) | 0.0107 | (0.0049) | |||
| ΔwF,t−1 | 0.0109 | (0.0051) | 0.0108 | (0.0061) | 0.0086 | (0.0036) | |||
| ΔwF,t−2 | −0.0025 | (0.0059) | −0.0037 | (0.0078) | |||||
| Δpt | −0.2650 | (1.2273) | |||||||
| Δpt−1 | 0.2494 | (0.6022) | |||||||
| Δpt−2 | −0.0374 | (0.6490) | |||||||
| rt | −0.0074 | (0.0088) | |||||||
| rt−1 | 0.0018 | (0.0079) | −0.0056 | (0.0022) | |||||
| rt−2 | −0.0054 | (0.0049) | |||||||
| χ2(l – k) | 0.2169 | 0.1528 | 0.4957 | ||||||
| SSC(Δyt) | 0.5440 | 0.5223 | |||||||
| SSC(ΔwNF,t) | 0.6113 | 0.7087 | |||||||
| SSC(ΔwF,t) | 0.5061 | 0.5904 | 0.3443 | ||||||
| SSC(Δpt) | 0.5226 | ||||||||
| SSC(rt) | 0.8767 | ||||||||
| σ | 0.0156 | 0.0164 | 0.0149 | ||||||
|
Note: See Table 3. |
|||||||||
Model (9) of Table 5 includes the change in the relative price of non-durables and two lags of this variable. The instrument set is unchanged from before. While the sum of the coefficients for this variable and its lags is negative, as we might expect, the coefficients are individually and jointly insignificant. Moreover, if we include contemporaneous or lag values of this variable individually, the coefficients are still insignificant. For this sample, then, there appears to be no significant contribution from changes in the relative price of non-durables.
Models (10) and (11) of Table 5 include the real interest rate (in levels) and two lags of this variable. The interest rate is calculated as an ex post measure using the 90-day bank bill (last observation of quarter) and four-quarter-ended inflation, where inflation is measured using the non-durables deflator for consistency. (Using the total consumption deflator provides essentially the same results.) The instrument set is as before. Model (10) is the general model, which is simplified by sequential elimination of statistically insignificant variables to obtain model (11).
In the general specification, the current and lagged values of the interest rate are insignificant. This appears to be a co-linearity problem, however, as the first lag is significant in the simplified version of the model. Although insignificant, including the interest rate variables does have a number of important effects on the general model. First, the error correction coefficient is much larger than that of model (4), with the implication that the adjustment to shocks is now predicted to be much quicker. The second interesting result is that the coefficients on net financial wealth are virtually unchanged. So, relative to model (4), the effects of shocks to net financial wealth are similar in impact but consumption adjusts much more rapidly toward the long-run effect. The other result of interest is that the change in non-financial wealth, lagged one period, is now significant. Although the coefficient is less than zero, the net effect of a change in non-financial wealth, including the effects through the error correction term, is positive.
The simplified model preserves all of these features except that the real interest rate, negatively signed, is now statistically significant lagged one period. Two other features emerge. First, changes in labour income are not a significant determinant of consumption, in contrast to what we find in model (4). Second, the dynamics are quite different. The change in consumption lagged two periods is now significant, so that consumption changes are quite persistent. This is somewhat difficult to interpret; possibly it reflects some form of habit persistence.
Overall, the fit and specification of model (11) is superior to model (4). First, the error correction term plays a more substantive role, which accords more closely with our expectations. Second, we can compare the R2 measures for each equation (not reported). In the context here, these should be interpreted as the simple correlation measure between the predicted and actual values. For model (4), the measure is 0.24; for model (11), the measure is 0.40. Finally, the standard error of the equation is smaller, 0.0149 compared to 0.0171 of model (4).
To better characterise the relationship between consumption and wealth, we now consider the effect of a permanent one per cent increase to either net non-financial wealth or net financial wealth. In each case, the increase in the net wealth measure is approximately one half of one standard deviation for the respective variable (in changes). To calculate these effects, we use model (11).[22] The results are presented in Figure 5. In each case, the response of consumption is measured in percentage terms relative to the level of consumption in 1999:Q3.
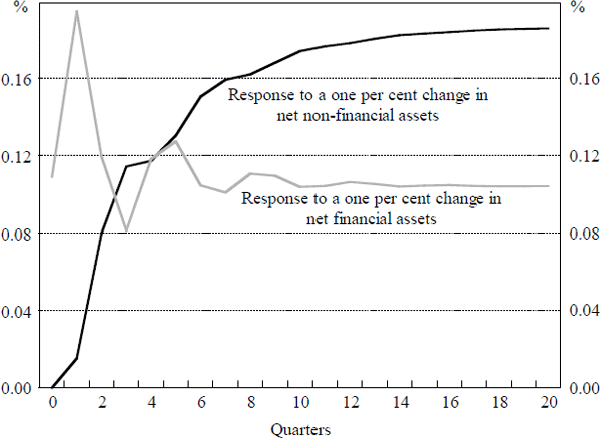
For a change in non-financial wealth, we observe a steady increase in non-durables consumption to a new level approximately 0.2 per cent higher than in the period of impact. The adjustment is reasonably rapid with roughly one half of the increase achieved after three quarters. For net financial wealth, the long-run effect is smaller, reflecting the smaller total value of financial assets; non-durables consumption rises to just over 0.1 per cent higher than its original pre-shock level. There are two key differences relative to the effects of an increase in non-financial assets. First, there is an immediate and significant impact on consumption in contrast to the slower increase arising from a change in non-financial wealth. Second, consumption overshoots its new long-run level; in the quarter after the initial increase, consumption is 0.2 per cent higher, falling back (roughly) to the new long-run level after two to three quarters.
There are some further remaining issues that we can usefully address. The first is how the model explains the behaviour of consumption in recent years. The second is whether the important share market floats and demutualisations of recent years had any implication for consumption beyond what is captured by changes in household wealth.
One of the motivations for this paper is the recent strong growth in consumption and how this relates to household wealth. The empirical models suggest that both financial and non-financial wealth have a statistically significant impact on consumption but it would be useful to know the economic significance of these variables. To do so, we consider some simple counterfactual experiments for the years 1997–1999.
Table 6 presents the annual growth rates for non-durables consumption, net non-financial wealth and net financial wealth as well as total net wealth for these years. Also reported are average growth rates for these variables over the sample.[23]
| Counterfactual experiments | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Constant growth in net wealth measure: | ||||||||
| (1) Non-financial | (2) Financial | (3) Total | |||||||
| Net wealth | |||||||||
| Year | Non-financial | Financial | Total | Consumption | Consumption | ||||
| 1997 | 8.5 | 11.7 | 9.7 | 2.3 | 2.2 | 1.8 | 1.7 | ||
| 1998 | 8.6 | 6.9 | 8.0 | 2.5 | 1.5 | 2.2 | 1.2 | ||
| 1999 | 10.2 | 9.5 | 10.0 | 3.3 | 2.4 | 2.7 | 1.9 | ||
| Avg | 3.5 | 4.8 | 3.9 | 2.1 | |||||
|
Notes: All variables are in real per capita terms. Average growth rates are for the sample 1988:Q4–99:Q4. The counterfactual results are derived using Model (11), Table 5. Experiment (1) sets the growth of net non-financial wealth to its sample average and all other RHS variables to actual values. Experiment (2) sets the growth of net financial wealth to its sample average and all other RHS variables to actual values. Experiment (3) sets the growth of both net non-financial and financial wealth to their sample averages and all other RHS variables to actual values. |
|||||||||
Over these three years, all measures of wealth and consumption have grown at rates greater than average for the period. In each experiment, we set the growth rate of one or both of the wealth measures to its average over the whole sample with all of the other determinants of consumption growth set to their actual values. The estimated model is then used to calculate a counterfactual path for consumption. In the first experiment, non-financial wealth is restricted to grow over the period 1997–1999 at its average rate of 3.5 per cent. The initial impact of the slower growth in consumption is small but the effect on growth rates in the last two years is substantial; in 1998, consumption growth is a full one per cent lower and in 1999 it is nearly the same again.
The effect of reduced growth in financial assets is also quite substantial and, because of the strong contemporaneous correlation between consumption and financial wealth, the effects are more immediate. In the first year, consumption growth is nearly one half of one per cent lower; in 1998 the effect is not very large but in 1999 consumption growth is more than one half of one per cent lower. The final experiment has both components of wealth growing at historical averages and, as we expect, consumption growth is significantly lower than actual growth. Taken together, these experiments suggest that a great deal of the strong growth in consumption in recent years can be attributed to higher than average growth in household wealth.
To better understand the effects of two of the more important recent share market events, the initial partial privatisation of Telstra in November 1997 and the demutualisation of AMP in June 1998, Figure 6 plots predicted values and the residuals for model (11). For both of these events, it is difficult to know with any certainty the effect on household net wealth. Since the acquisition of the assets in both instances largely involved a re-balancing of household balance sheets rather than an increase in net financial wealth, it is likely that the net effect in each case is small. There may, however, have been a positive effect on household wealth due to capital gains since there was a strong rise in price after both listings.[24] Gauging the net effect of this on household wealth is difficult, however, in part because of timing issues and in part because households also have equity in the financial institutions themselves.
me hypothesis, consumption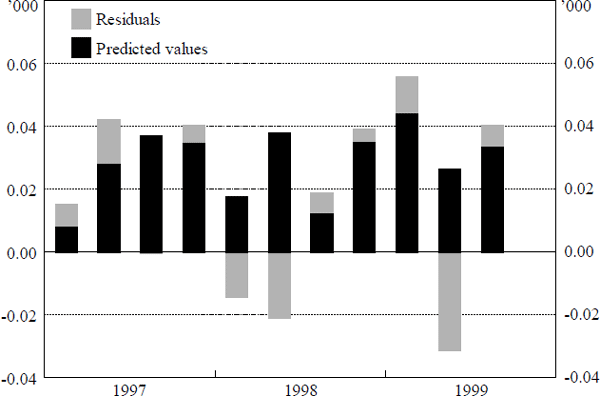
Although we cannot usefully determine the contribution to net financial wealth of either of these two events, it is possible to consider whether they had any extraordinary effects on consumption either as a consequence of the strong and immediate capital gains made on visible and liquid assets or their implications for consumer confidence. For these reasons, we might expect the model to under-predict consumption in these or subsequent quarters. In fact, however, there is no evidence of such effects from either event. For the December quarter 1997, relevant for the Telstra privatisation, the model does under-predict consumption but by a very small amount (the standard error of the residuals is 0.015, see Table 5, and the residual for this quarter is approximately one third this size). For the June quarter 1998, relevant for the AMP float, the model over-predicts consumption. Thus for both cases, there is minimal evidence of a liquidity or confidence effect.
The emphasis so far has been on an empirical model for consumption so that we can gauge the effect of changes in household wealth. It is useful, however, to put our empirical models in a broader perspective and consider explicitly what information our results provide regarding theories of aggregate consumption. This is consistent with the vast majority of the recent empirical literature on aggregate consumption, which has as its focus the testing of the permanent income model (and to a lesser extent, the life cycle model) and, when rejected, the likely source of failure.
The first and most straightforward conclusion from the models of Tables 3–5 is a rejection of the simple permanent income model. In each of the models we estimate, there is evidence that consumption changes can be predicted by past information.[25] This conclusion is consistent with most empirical studies, both for Australia and overseas, beginning with Hall (1978).
One focus of the recent empirical literature concerns the excess sensitivity of consumption to changes in labour or disposable income; that is, current and lagged differences of income measures are significant predictors of changes in consumption (see for example the cross-country study Campbell and Mankiw (1991)). A standard explanation for this type of excess sensitivity is the presence of consumers that are either liquidity-constrained or rule-of-thumb consumers who simply consume a proportion of their current income. Deaton (1992) provides a discussion of this interpretation and the associated empirical literature.[26] Debelle and Preston (1995) find evidence in favour of this hypothesis for Australian consumption growth. In contrast, however, de Brouwer (1996) and Olekalns (1997) find no evidence of excess sensitivity in recent years for Australia and attribute this to the deregulation of financial markets. Olekalns makes this point most convincingly by demonstrating that prior to deregulation (the period 1959–1982), there is evidence of excess sensitivity of consumption to changes in disposable income while post deregulation (the period 1984–1995) there is no such evidence.
Our results, in particular model (4) of Table 3, provide mixed evidence in this respect. First, across all models that we estimate, we find contemporaneous changes in labour income to be insignificant. This is not consistent with the hypothesis that a proportion of the population follows simple consumption rules; nor does it sit well with the hypothesis that a significant fraction of consumers are liquidity-constrained. What we observe that is consistent with such behaviour is the significance of contemporaneous changes in net financial wealth. More importantly, this suggests that consumers treat components of household income differently. For example, one interpretation of our results is that changes in net financial wealth are treated as windfall gains directly boosting consumption. An alternative explanation is a dependence of consumption on consumer confidence, which is captured by the changes in financial wealth. We discuss this further below.
The significance of the lagged real interest rate suggests that the assumption of a constant real interest rate is not a particularly good one, which should not come as any real surprise. More importantly, however, relaxing this assumption is not sufficient to reconcile the permanent income/life cycle models with the Australian data. Even when we condition on this variable, as implied by the more general version of the theory, we still find other variables predict consumption changes, in contrast to the predictions of the theory.[27]
In the context of the life cycle model, Gali (1990) and Clarida (1991) demonstrate that some of the stronger predictions of the permanent income model are overturned. In particular, changes in consumption are predictable by lagged changes in labour income and the error correction term (c – y) . In this case, we get some weak evidence in favour of the life cycle model in Table 4 where the error correction term is weakly significant and the lagged first difference of labour income is significant. Where the model fails, however, is the significance of the net financial wealth terms, which is not predicted by the life cycle model. A further source of failure is the fact that the more general error correction term involving net wealth is a significant determinant of consumption changes (that is, the models of Table 3 and 5) and that this term is more significantly correlated with consumption changes.
By way of summary, we see the sensitivity of consumption to the components of net wealth as the most important departure of our results from standard intertemporal consumption theories. The other significant variables of the models can possibly be explained by unspecified dynamics (in the case of the error correction terms), aggregation and life cycle features (the error correction terms, the lagged differences of labour income) or non-constant real returns. In contrast, existing consumption theories do not provide an explanation for why predicted changes in net wealth (based upon past information) should affect current changes in consumption nor why they should do so differently from predicted changes in labour income. Interestingly, our results are similar to Hall's (1978) seminal study of the permanent income hypothesis. Of the variables that he considers, only changes in equity price indices (closely related to our measure of net financial wealth) predict consumption changes. Hall downplays this result as evidence against the permanent income hypothesis, arguing that the empirical contribution of equity price changes for predictions of consumption changes are very small. This contrasts with our results, where the contributions of changes to net wealth appear to be quite large.
Following a number of recent studies for the United States, Otoo (1999) and Starr-McCluer (1998), one possible explanation for our results may be the correlation between equity market values and consumer confidence. That is, our results are identifying a link between consumer sentiment and consumption spending, with the former proxied by net financial wealth, rather than a link between consumption and a component of household income. Unfortunately, it is extremely difficult to identify cause and effect in this context and we leave investigation into this aspect of consumption behaviour for future research.
Footnotes
See Appendix A for details of the data. Household consumption expenditure includes a measure of imputed rent for owner-occupiers, creating a possible link between household assets and consumption. As the link will depend upon market factors, it is difficult to control for this. We are unwilling to remove the imputed rent measure from consumption in part for simplicity and in part because we are left explaining a specialised measure of consumption of little interest. [8]
Theoretical models of consumption are based upon a flow measure of consumption, which is why we use non-durable consumption expenditure. Non-durable consumption expenditure is approximately 86 per cent of total consumption and the two series share very similar time series properties. [9]
A natural direction to pursue is a further disaggregation of financial assets, as some asset groupings may be more liquid than others. Most notably, assets in life and pension funds, which are a significant proportion of household financial assets, are not liquid for most households. Further, changes in the values of these assets, particularly for pension assets supporting defined benefits schemes, may not be very visible to households. Our treatment assumes that all financial assets are fungible and that households respond uniformly to changes in the value of financial assets irrespective of the source. [10]
Over the whole sample, there is conflicting evidence as to whether net wealth is first difference stationary. The main difficulty is obtaining a finite autoregressive representation of differenced net wealth that is free from serial correlation. [11]
To the extent that the current rise in household wealth is based upon housing, as was the case in the late 1980s, this is not the ideal strategy. As will become apparent below, however, attempts to model the entire sample, and so more completely model this episode, are not very fruitful. [12]
For detail on the deregulation and development of Australian financial markets through the 1980s and early on 1990s, see Edey and Gray (1996). [13]
Given the evidence of structural change, it is perhaps misleading to refer to these as steady-state relationships; however, this is exactly what these are for the dynamic models of consumption. This terminology seems preferable to identifying these as long-run relationships, which they clearly are not. [14]
The theoretical models usually assume that labour income is an exogenous first difference stationary stochastic process; under usual simplifying assumptions, this implies that consumption and wealth are first difference stationary processes. [15]
See Hamilton (1994, pp 608–610). [16]
The estimates are obtained by nonlinear LS methods. An AR(1) process was found to be sufficient. For the Newey-West covariance estimator we set the lag truncation parameter for the autocovariance function to be two. [17]
If Equations (2) and (3) are estimated using total consumption as the dependent variable the results are similar to those presented in Table 2 (these are available from the authors upon request). [18]
Hall (1988) and others suggest using instruments lagged twice or more to avoid a time aggregation issue. If consumption follows a random walk but the decisions are made at a higher frequency than measured consumption, then measured consumption will have a first order moving average error process; see Working (1960). We are more concerned, however, with instrument quality, which is likely to be greater with variables lagged one period. To some extent, we can test whether the instrument set we use is valid by testing the over-identifying restrictions of the model. If the instruments are not valid then we should reject these restrictions. [20]
As described in Davidson and Mackinnon (1993, p 612). None of the principal conclusions depends upon the use of this estimator. [21]
The exercise we consider assumes that all of the adjustment occurs through changes in consumption. An alternative approach would consider the system as a whole, allowing consumption, labour income and wealth to adjust to deviations from the steady state. We leave this as a direction for further research. [22]
The calculations in Table 6 are based upon more recent data that includes 1999:Q4. Because much of the data must be constructed (see data appendix), we have chosen not to update our estimation with this more recent data. The data and calculations for Table 6 are available upon request. [23]
For the Telstra privatisation, the acquisition of the shares by households involved some mixture of a fall in household consumption expenditure, a sale of other assets and an increase in liabilities. Abstracting from subsequent capital gains, only in the first instance is there the possibility of a positive effect on net financial wealth but the model is not well suited to describing the interaction between saving and consumption in this instance. For consumers on aggregate to substantially alter their saving decisions in this way suggests that they were previously constrained from such decisions, something not easily captured in our empirical model. For the other two, the effects broadly cancel out. A similar argument holds for the AMP demutualisation; prior to this, AMP was already an asset listed on household balance sheets. Again, of course, this argument abstracts from capital gains after listing. [24]
One aspect of our estimation that differs from other studies, e.g. Campbell and Mankiw (1990), is our use of foreign variables as instruments and the fact that these are not lagged back two periods to avoid time aggregation issues. Although we provide some empirical support for our instrument set, there may be some concern about these results when the focus is explicitly testing the permanent income model. To see if our results are robust in this direction, we re-estimate the model using the same instrument set lagged two periods. The results are largely unchanged. [25]
The significance or otherwise of current income is at best an informal test of whether or not a significant proportion of the population is liquidity-constrained. Liquidity constraints have other implications that must also be tested. See Deaton (1992) for further detail. [26]
A number of authors have sought to determine if relaxing the assumption of a constant real interest rate can explain the excessive sensitivity of consumption. See Campbell and Mankiw (1990) for further discussion. Note that our regressions are not strictly designed to test the general PI model; to do so, requires careful specification of the timing of asset returns and information available to consumers (see Hall (1988)). Nonetheless, what we observe is broadly consistent with the prediction that current consumption falls as the real interest rate rises. [27]