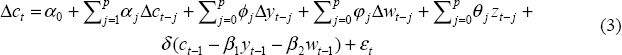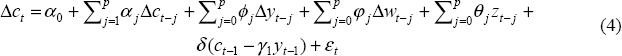RDP 2000-09: Consumption and Wealth 2. Aggregate Consumption Models

Our objective is to examine the empirical relationship between consumption and wealth and for this we estimate fairly traditional aggregate time series consumption functions. Following other empirical studies of consumption, notably Blinder and Deaton (1985) for the US and Davidson and Hendry (1981) for the UK, we use flexible distributed lag models that incorporate steady-state relationships between consumption and household income or its components. This allows us to examine both the long-run steady-state relationship between consumption and household income, including the return on household wealth, as well as the short-run dynamics of consumption.

The empirical models we estimate are quite general and encompass a number of theoretical models of consumption. In particular, we are able to examine the predictions of the permanent income hypothesis, originally associated with Friedman (1957) and examined extensively in studies by Hall (1978), Flavin (1981) and Campbell (1987) among others. We are also able to examine the more flexible treatment of the permanent income hypothesis that allows for some proportion of aggregate consumption to reflect liquidity-constrained or ‘rule-of-thumb’ type consumers (see, for example, Campbell and Mankiw (1990)). Our empirical models also encompass the life cycle hypothesis, associated with Modigliani and Brumberg (1954), and the more recent treatments of this model by Gali (1990) and Clarida (1991).^[3]

In levels we consider two long-run or steady-state relationships. These are:

where c is consumption, y is household labour income (after tax), and w is household net asset wealth. All variables are in levels and in real per capita terms. In each, v is a stationary disturbance term, possibly correlated with household labour income and wealth. At the simplest level, we can motivate these relationships as designed to capture any persistent empirical relationship between consumption and income. More interestingly, both can be motivated by the theories of consumption discussed above. Equation (1) is consistent with both the permanent income model and the life cycle model, although the interpretation of the coefficients differs somewhat between the two models. The steady-state condition in Equation (2) is less general, arising in the life cycle model presented in Gali (1990). For the empirical discussion that follows, it is useful to develop briefly the predictions of the permanent income and life cycle model as they relate to Equations (1) and (2) as they provide some guidance in the specification of the empirical models.

Both the life cycle and permanent income model are centred on forward-looking consumers that optimally choose consumption as a function of current and future expected income. In each, the level of current consumption is proportional to the level of current household income, comprising labour income and the return on household assets, and the present discounted value of expected future labour income. Under certain simplifying assumptions, most notably a constant real interest rate, this implies a long-run relationship of the form in Equation (1). Further, we anticipate the coefficient on β₁ to be close to one and the coefficient on β₂ to be comparable to a real interest rate measure adjusted for taxes. As a point of reference, under the permanent income model with the assumption that consumers discount the future at the same rate as implied by market interest rates, consumption is exactly equal to permanent income; this implies that β₁ is equal to one and β₂ is an estimate of the real after-tax rate of return on household assets.^[4]

The steady-state condition in Equation (2) arises in the life cycle model presented in Gali (1990). Under the standard assumptions of a constant real interest rate and consumption equal to permanent income, this paper shows that if labour income is assumed to be stationary in changes, I(1), then aggregate consumption is also I(1) and the two series are cointegrated (a linear combination of these two variables is stationary) with cointegrating vector (1,−γ₁). The coefficient on labour income depends upon, among other things, the demographic variables of the model and is expected to be close to one but not necessarily less than one.^[5]

Notice that with respect to modelling the relationship between consumption and wealth, Equation (1) is directly of interest since it provides information concerning the long-run relationship between these variables. Equation (2), in contrast, does not provide any such information but nevertheless may be useful in modelling consumption. Certainly if the life cycle model is correct, then the correct dynamic model for consumption has this condition as the error correction term.

Conditional on these two steady-state conditions, the consumption models we consider are error correction models of the form:

where z_t is a vector of other possible determinants of consumption such as real interest rates and other relative price variables.

Equation (3) is motivated by the permanent income model under which all of the coefficients on the lagged variables should be zero, as should the parameters on the contemporaneous variables once we control for the endogeneity of these variables. This is Hall's (1978) insight that under the permanent income hypothesis (and a constant real interest rate), changes in consumption are not predictable; optimal consumption decisions should reflect all current information. If we relax the constant interest rate assumption, then changes in consumption may be correlated with the level of the real interest rate (see Hall (1988)).

Equation (4) is motivated by the life cycle model but nests the permanent income model as well, under which all of the right hand side variables should be insignificant (assuming a constant real interest rate). Under the life cycle model, however, this is not the case. Because aggregate consumption reflects decisions by cohorts at different stages of their life cycle, Gali demonstrates that the error correction term in Equation (4) should predict changes in consumption; further, lagged changes in labour income should also predict changes in consumption.^[6] This contrasts markedly with the permanent income model where consumption changes, under the same conditions on consumers' preferences, are unpredictable.^[7] What is still true, though, is that the contemporaneous variables should be insignificant.

The role of the contemporaneous variables in Equations (3) and (4) merits further comment. Although not implied by either the permanent income or life cycle model, there are good reasons to include these variables. Firstly, a strict interpretation of theory may be a poor guide and since our objective is empirical it seems sensible to allow for as general a structure as possible. Secondly, if individuals are liquidity-constrained or not forward-looking rational consumers, then consumption may respond to changes in current income. This conjecture has been the focus of a number of studies, for example Campbell and Mankiw (1990, 1991). Recent Australian studies are Olekalns (1997), de Brouwer (1996), and Debelle and Preston (1995). Finally, as discussed above, if the objective is to test either the permanent income or life cycle model, then a perfectly valid test is whether or not predicted values of labour or asset income explain changes in consumption; see Blinder and Deaton (1985) and Deaton (1992).

Footnotes

For the life cycle hypothesis, see also Ando and Modigliani (1963) and the survey article Modigliani (1986). Deaton (1992) provides an excellent summary of the macroeconomic consumption literature. [3]

This discussion overlooks much of the theoretical detail of the permanent income and life cycle models, including important distinctions between the two. For purposes of interpreting Equation (1), the distinction between the two theories is largely irrelevant. While it does affect the strict interpretation of the parameter estimates and consequently the magnitudes we might expect, it is doubtful that one can discriminate between the two models using aggregate consumption data. For a more detailed discussion of the long-run predictions of the permanent income model, see Campbell (1987). For the life cycle model, see Gali (1990), which has the attractive feature of providing a theoretical model that encompasses both the life cycle model and the permanent income model. An important assumption that generally underlies both these theories is that labour income is exogenous and first difference stationary; this is implicit in much of our discussion. [4]

See Gali (1990) for further detail. The demographic variables arise in life cycle models because of the finite life of agents and their declining productivity, neither of which feature in the representative agent permanent income model. In his paper, Gali directly estimates γ₁ to be 1.04 for the US. Alternatively, his calibrations imply a value as high as 1.11. A value of one is a reasonable benchmark. [5]

In a different modelling framework but for similar reasons, Clarida (1991) also demonstrates the predictability of consumption by lagged changes in income. [6]

Very simply, the intuition for this result is that the labour income and consumption of new cohorts are both predictable. In more detail, we can motivate the error correction term in Equation (4) as follows. At time t−1, expected aggregate consumption at time t is a weighted average of expected consumption by existing consumers and the expected consumption by new consumers arriving at time t. The former is equal to consumption of the existing cohort at t−1; this is Hall's result. The second component, however, is a function of the new cohort's expected lifetime labour income (assuming no initial assets). As a result, aggregate consumption does not follow a random walk; rather aggregate consumption will be dependent upon variables that forecast next period's labour income as well as upon past consumption. The solution is an error correction model for aggregate consumption with past consumption and past labour income, as a predictor of future labour income, forming the error correction term. [7]