RDP 2000-02: Forecasting Australian Economic Activity Using Leading Indicators 3. Results
April 2000
- Download the Paper 339KB
3.1 Data
We consider three measures of economic activity: real GDP, employment and unemployment, all seasonally adjusted. The specific details of these series are presented in Appendix A. Of the activity series, GDP is published quarterly while employment and unemployment are published monthly. Of the leading indices, the ABS leading index is published quarterly while the WM and NATSTAT leading indices are published monthly. All variables are expressed in logarithms except for the ABS index and unemployment. The former is used as published. The latter is measured as a proportion of the labour force (for example, a seven per cent unemployment rate is 0.07).
We let the activity variable dictate the frequency of the data we use to estimate the model. So the GDP models are quarterly while the employment and unemployment models are monthly. The sample periods used in the estimation vary depending upon which index and which activity variable is being considered. The choice of sample is always based, where possible, on the full sample for each index, which are identified in the previous section. The exact samples used are identified in the tables and figures below.
The frequency of the series and the timing of their release are important for how we construct and interpret our forecasts. GDP and the ABS leading index are available on a quarterly basis and are published two months after the reference period. The WM index, which is monthly, is also published two months after the reference period. So, two months into a quarter, we have access to all of the previous quarter's WM index figures. The NATSTAT index is also available monthly but with a three-month publication lag. For quarterly forecasts of GDP, we use quarterly averages of the WM and NATSTAT indices.[7] According to the publication times of these variables and the way we average them, our forecasts should be interpreted as being calculated in the third month of the quarter following the reference quarter. So, for example, by mid-June we have data for each series for the first quarter of the year. This means that the one-step ahead forecasts from our quarterly models are for the quarter nearing completion.
Employment and unemployment are published on a monthly basis and are released with a one-month lag. The two indices that are available monthly are the WM index and the NATSTAT index but these are released with a greater lag than employment and unemployment. The WM index has a two-month lag while the NATSTAT index is slightly longer. Typically, when either index becomes available for a particular reference month, we will have unemployment and employment figures for the two subsequent months. So, in practical terms, we are really only interested in forecasts three or more months ahead from these monthly models.[8]
For within sample evaluation of the indices, and to a lesser extent the out of sample evaluation, it is necessary to characterise the time series properties of the activity series and the leading indices. The NATSTAT and ABS indices, published as deviations from trend, are stationary by construction. In contrast, GDP, employment, unemployment and the WM index are all possibly non-stationary and may require suitable transformations for estimation.
Unit root tests and tests for cointegration are presented in Appendix B. For GDP, the results are ambiguous as to whether GDP has a unit root or is trend stationary. As it is hard to distinguish between a first difference stationary process and a trend stationary process, and given our interest only in forecasting ability, we consider both possibilities. For the quarterly average of the WM index, we find evidence of a unit root. Under the assumption of a unit root in GDP, we also test for and find evidence of a cointegrating relationship between GDP and the WM index. Accordingly, we also consider a vector error correction model (VECM) for these two series. For the monthly data, over the relevant sample periods, we find evidence of a unit root in all three series, employment, unemployment and the WM leading index. We find, however, no evidence of cointegration.
3.2 Within Sample Evaluation
For each leading index, and for the measures of activity, we estimate two variable VAR models over the full sample of data available. In each case, the bivariate VAR provides information about the relationship between the two series. Specifically, we can determine whether the leading index is a useful predictor of the activity variable – that is, whether it Granger causes the activity variable. In addition, we can examine the timing of the relationship between the two series and the relative importance of each series for forecasting the other series in the model. The impulse response functions and the forecast error variance decompositions are the easiest way to summarise these two aspects of the relationship.
For simplicity, we restrict this within sample evaluation to simple VAR models in first differences (except for the NATSTAT and ABS indices for reasons explained above). The exact sample and the choice of lag length for each model are identified in Table 2, which presents Granger causality tests for the three activity series and the three leading indices. We do not engage in a detailed specification search for the lag length, instead fixing a lag length sufficient to ensure that the innovations to the VAR models are white noise.[9]
| GDP Model (p = 8) | WM | NATSTAT | ABS |
|---|---|---|---|
| 1960:Q1–1999:Q1 | 1967:Q1–1999:Q1 | 1971:Q1–1999:Q1 | |
| GDP → Leading index | 16.2056 (0.0395) |
8.1570 (0.4183) |
9.6980 (0.2869) |
| Leading index → GDP | 34.8662 (0.0000) |
23.5325 (0.0027) |
19.1288 (0.0142) |
| Employment Model (p =14) | 1966:M7–1999:M4 | 1966:M12–1999:M4 | |
| EMP → Leading index | 18.1863 (0.1984) |
14.1925 (0.4355) |
– |
| Leading index → EMP | 54.2861 (0.0000) |
31.9531 (0.0041) |
– |
| Unemployment Model (p = 14) | 1959:M9–1999:M4 | 1966:M12–1999:M4 | |
| U → Leading index | 20.7620 (0.1079) |
24.5250 (0.0396) |
– |
| Leading index → U | 64.9988 (0.0000) |
26.7686 (0.0206) |
– |
|
Notes: The GDP model is estimated using quarterly data and the employment and unemployment models are estimated using monthly data. All sample periods are determined by data availability. The Granger Causality test statistics are for the hypothesis that the coefficients on the lags of variable y are jointly zero in the VAR equation for variable x. The alternative is that the lags of y help predict variable x, denoted y → x in the table. The test statistic is distributed χ2(p), where p is the lag length. Marginal significance levels are in parentheses. |
|||
For GDP, we can reject the null hypothesis that the coefficients on the leading indices are jointly equal to zero at standard significance levels. Consequently, all three indices are useful predictors of future GDP. Interestingly, we also find evidence that GDP is a useful predictor of the WM index. This type of feedback between activity and the WM index is also noted in Trevor and Donald (1986). While not of direct interest itself, it does have possible implications for forecasting with the VAR, which requires forecasts for both variables. The strong relationship between these two series suggests that the VAR forecasts may perform quite well.
For the two monthly series, employment and unemployment, we only use the WM and NATSTAT indices as the ABS index is not available monthly. We find that these two leading indices are useful predictors of both employment and unemployment. We also find evidence of feedback, this time between the NATSTAT leading index and unemployment. All together, these results are reasonably encouraging: the three leading indices all seem to have some predictive content for the three measures of activity we consider here.
An understanding of the timing of the relationship between the series is available from the impulse response functions. The specifications for the VAR models are the same as those described in Table 2. Figure 2 presents the response of real GDP growth to an orthogonalized innovation to each of the three leading indices.
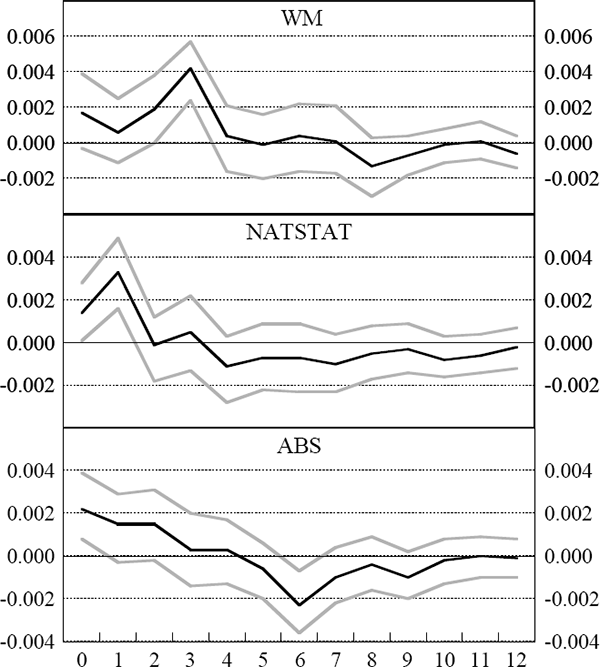
Notes: The figure shows point estimates and 90 per cent confidence intervals of the impulse responses of GDP to one standard deviation increases in the various leading indices. These impulse response functions are estimated from two-variable VARs in first differences with lag lengths and sample periods as described in Table 2. The confidence intervals are calculated by a simple bootstrap procedure involving 500 draws with replacement from the empirical distribution of the VAR innovations.
Figure 3 does the same for employment growth and the change in unemployment. In all cases, the VAR models are ordered with the leading index first. While in principle these responses are not invariant to the ordering of the variables in the VAR, empirically the conclusions are not substantially altered if the ordering is reversed.
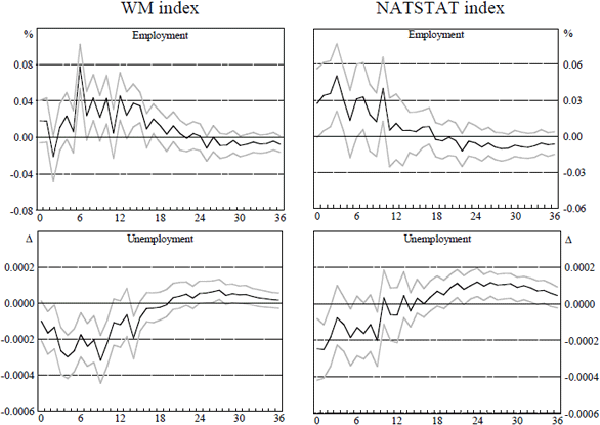
Notes: The figure shows point estimates and 90 per cent confidence intervals of the impulse responses of employment and unemployment to one standard deviation increases in the WM and NATSTAT leading indices. These impulse response functions are estimated from two-variable VARs in first differences with lag lengths and sample periods as described in Table 2. The confidence intervals are calculated by a simple bootstrap procedure involving 500 draws with replacement from the empirical distribution of the VAR innovations.
For GDP, an innovation to the WM index has the greatest impact three quarters later (the innovation occurs in period zero of the figure). The other two indices have a smaller lead in that the maximum impact of an innovation occurs much more quickly. In the case of the NATSTAT index, the maximum impact occurs after one quarter while for the ABS index, the maximum impact is contemporaneous (with a subsequent significant negative impact after six quarters). In all cases, the effects of innovations in the leading indices on the activity variables are statistically significant at their maximum impact, consistent with the Granger causality results.
In Figure 3, we present the responses of employment and unemployment to innovations to the WM index and the NATSTAT index. These tell a similar story to those in Figure 2. The WM index has a significant impact on employment after six months. For unemployment, the maximum effect occurs anywhere from five to nine months after the innovation. For the NATSTAT index, we observe the maximum effect on employment after three months and contemporaneously for unemployment. In effect, there is no real lead time of this index for these series (given publication lags). Recall that for both of these leading indices, unemployment and employment for the first two months after the innovation are known so that the lead times are less than the figures suggest. Overall, the important result from Figures 2 and 3 is the substantial advantage in lead time that the WM index has over the other two indices.
We also calculate forecast error variance decompositions for the VAR models described in Table 2. These decompositions indicate the proportions of the forecast error variance of the activity variable accounted for by its own innovations and by those of the leading index in each model. This provides information about the relative importance of the leading index in explaining variation in the activity variables. For simplicity, we present a brief summary of the full results reported in Appendix C. For all of the activity variables, the indices make a relatively small contribution to the variability of the activity variable itself. This suggests that for prediction, what really matters is the relationship between the activity variable of interest and its own history. We return to this issue of relative contribution when we consider the out of sample forecasting performance in the following section.
3.3 Out of Sample Evaluation
Our principal objective is to evaluate the contribution of leading indices towards forecasts of activity. The within sample evaluation of the previous section provides some information in this regard but it is limited. A much more informative assessment of forecasting models is based upon out of sample forecasting performance. In the forecasting literature, this is the preferred means of evaluating forecasting models. (See for example, Granger (1989).) In the current context, this presents a problem. For within sample evaluation, we have established criteria, such as the Granger causality tests. For out of sample evaluation of the leading indices, however, there is no obvious procedure. In effect, we have to make some commitment to a particular forecasting model. As a result, our conclusions are a function, to some extent, of the models we choose to generate forecasts.
We see the simple two variable VAR models as a natural framework to pursue our objective. We recognise that these are not ideal forecasting models and that the models we present could easily be improved upon.[10] Nevertheless, these models have a number of advantages for our purposes. First, they are simple and transparent so that it is relatively easy to determine the contribution of the leading index to the quality of the forecasts. Second, these are closed models in the sense that they do not depend upon any exogenous variables (apart from deterministic variables). This again makes it easy to focus attention on the contribution of the leading index. Finally, these models require relatively little specification (choice of lag length is the primary specification issue) and this makes them convenient for a study such as this which considers a number of activity variables and indices.
There is a further reason to consider these time series models. They are simple and convenient models in which to use the leading indices for forecasting. In this sense, they are consistent with the leading indicator methodology (to the extent that we wish to use these indices to explicitly forecast activity variables). From this perspective, it seems natural to consider further how these VAR models using leading indices perform. To pursue this, we consider the forecasting performance of these models for GDP relative to a single equation structural model of GDP presented in Gruen and Shuetrim (1994).
The discussion below has two parts. The first focuses on the contribution of the three leading indices for forecasting GDP, employment and unemployment. The second pursues the comparison of the leading index models to the Gruen and Shuetrim model.
3.3.1 Contribution of leading indices
We measure out of sample forecast performance by root mean squared prediction errors, RMSE statistics.[11] These statistics are calculated as follows. An initial estimation sample is chosen, the model is estimated and one-step to s-step ahead forecasts for the activity variable are calculated. The prediction error for each forecast horizon is calculated by taking the difference between the forecast and the actual data. This procedure is repeated for the next sample ending one period later; again the prediction errors are calculated for each forecast horizon. This procedure continues until all available data has been used. In each case, the lag length of the model is fixed. From this procedure, we obtain samples of prediction errors for different horizons; for each horizon, we calculate the square root of the mean of the squared prediction errors (the RMSE). So that the RMSE statistics are comparable across models, they are always calculated using the predicted log-level of the activity variable.
The forecasting sample period we consider is 1990:Q1–1999:Q1 for the quarterly data and 1990:M1–1999:M4 for the monthly data. (So, for the quarterly data, the terminal date of our first sample is 1989:Q4.) As with the analysis in the previous section, the sample start dates depend upon the availability of data for the index variable and the activity variable in question. (The exact samples used are specified in the tables.) For both the quarterly and monthly data, we consider a two year forecast horizon.
A strict evaluation of out of sample forecasts has very demanding data requirements. Notably, we should use data of the vintage corresponding to the sample period we are estimating so that we mimic real time forecasting exercises. We are unable to satisfy this requirement. For all of our experiments we use current vintage data. This is most problematic for GDP, where we use a chain-linked GDP series that was not available until recently, and for the leading indices, which are regularly revised. This feature of our experiments, particularly the use of revised indices, is likely to bias our RMSE statistics downwards.
Depending upon the index and activity variable in question, we consider a number of different model specifications based upon the unit root tests and the tests for cointegration discussed previously. For the WM index and GDP, we consider a bivariate VAR in log-differences, in log-levels with a trend and a bivariate vector error correction model in log-levels (VECM).[12] For the other two indices and GDP, we consider a VAR in log-differences and in log-levels with a trend. These results are reported in Table 3.
| RMSE for forecast sample: 1990:Q1–1999:Q1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecast horizon (quarters) | |||||||||
| p | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| WM (1960:Q1–1999:Q1) | |||||||||
| Differenced | 2 | 0.0079 | 0.0122 | 0.0157 | 0.0192 | 0.0222 | 0.0249 | 0.0270 | 0.0286 |
| Trend | 2 | 0.0075 | 0.0112 | 0.0150 | 0.0183 | 0.0212 | 0.0238 | 0.0258 | 0.0272 |
| VECM | 2 | 0.0083 | 0.0122 | 0.0162 | 0.0195 | 0.0223 | 0.0248 | 0.0266 | 0.0278 |
| Naïve (differenced) | 4 | 0.0085 | 0.0133 | 0.0173 | 0.0208 | 0.0248 | 0.0282 | 0.0304 | 0.0320 |
| Naïve (trend) | 1 | 0.0078 | 0.0214 | 0.0165 | 0.0203 | 0.0235 | 0.0262 | 0.0280 | 0.0292 |
| NATSTAT (1967:Q1–1999:Q1) | |||||||||
| Differenced | 1 | 0.0075 | 0.0121 | 0.0162 | 0.0203 | 0.0238 | 0.0269 | 0.0293 | 0.0310 |
| Trend | 1 | 0.0086 | 0.0137 | 0.0178 | 0.0213 | 0.0242 | 0.0265 | 0.0279 | 0.0283 |
| Naïve (differenced) | 1 | 0.0076 | 0.0121 | 0.0162 | 0.0201 | 0.0236 | 0.0266 | 0.0288 | 0.0305 |
| Naïve (trend) | 4 | 0.0078 | 0.0124 | 0.0158 | 0.0194 | 0.0221 | 0.0242 | 0.0256 | 0.0265 |
| ABS (1971:Q1–1999:Q1) | |||||||||
| Differenced | 1 | 0.0071 | 0.0109 | 0.0143 | 0.0180 | 0.0213 | 0.0247 | 0.0278 | 0.0307 |
| Trend | 1 | 0.0080 | 0.0124 | 0.0157 | 0.0187 | 0.0212 | 0.0233 | 0.0250 | 0.0262 |
| Naïve(differenced) | 1 | 0.0075 | 0.0119 | 0.0160 | 0.0200 | 0.0235 | 0.0267 | 0.0292 | 0.0312 |
| Naïve (trend) | 4 | 0.0076 | 0.0121 | 0.0155 | 0.0192 | 0.0221 | 0.0244 | 0.0260 | 0.0270 |
| No change (growth) | – | 0.0095 | 0.0167 | 0.0232 | 0.0318 | 0.0390 | 0.0467 | 0.0554 | 0.0625 |
|
Notes: The lag length is p and is chosen to minimise the RMSE for our forecast sample at the eight-quarter horizon. All RMSE statistics are in terms of levels of the activity series. For the NATSTAT and ABS differenced models, only the activity variable is in differences. The naïve model is an AR(p) model in the activity variable, either in differences or in levels with a trend. |
|||||||||
Each model identified in Table 3 is estimated using different lag length specifications, p=1 to p=8. The RMSE results reported are those from the specification with the smallest RMSE at the eight-quarter horizon. The reason for doing this is that to evaluate the contribution of the leading index to the forecast quality, it seems most sensible to use the specification in each case that provides the best forecasting performance. We have chosen to focus on the longer horizon as our gauge of forecasting performance since this is generally of greater interest to policy-makers. Notice that choosing the lag length based upon within sample diagnostic tests does not generally provide the best forecasting model. Invariably, a much shorter lag length outperforms the same model with a longer lag length.[13]
A possible explanation for this result is that unrestricted VAR models are heavily over-parameterised and are likely to be estimated with a great deal of uncertainty. This uncertainty can result in poor forecast performance (see Fair and Shiller (1990)). By restricting the lag length of the model, we may reduce this uncertainty and still obtain reasonably good forecasts at all horizons. This is, in effect, the same argument that motivates the Bayesian VAR analysis (see for example, Robertson and Tallman (1999)).
Prior to assessing the contribution of the indices, it is useful to put the RMSE statistics into context. Consider the WM index and the VAR model in log-levels with a trend. The one-quarter ahead RMSE is 0.0075. This means that the average prediction error, in absolute terms, is 0.75 per cent of the level of GDP.[14] This maps directly into quarterly growth rates: the one-step ahead quarterly growth rate forecasts have an average prediction error of 0.75 per cent. This compares to an average absolute quarterly growth rate over the sample for which we are forecasting of 0.95 per cent. In this context, our prediction error is relatively large. For the four-step and eight-step ahead forecasts, the RMSE statistics are 1.8 per cent and 2.7 per cent in terms of the level of GDP. This maps directly into four-quarter ended and eight-quarter ended growth rates respectively. Again, to put this into perspective, the average of the four-quarter ended and eight-quarter ended absolute growth rates over our forecasting period are 3.4 per cent and 6.3 per cent respectively.[15] While still large, our forecast errors are smaller relative to the average absolute growth in GDP at longer horizons than at shorter horizons.
We now consider the contribution of each index. For the WM index, the VAR model with trend is the one with the best forecasting performance at all forecast horizons, although the gain relative to the differenced model or the VEC model is relatively small. To gauge the contribution of the leading index, we can compare the bivariate VAR model with trend to an AR model in GDP also estimated with a trend.[16] In the case of the latter, we again choose the lag length that provides the lowest RMSE statistic at the eight-quarter horizon. In this instance, we observe that the VAR model provides slightly better quality forecasts; the RMSE for the VAR is 0.0272 compared with 0.0292 for the AR model, an improvement of roughly seven per cent. A similar conclusion arises from comparison of the VAR model in differences (or the VEC model) to an AR model for GDP in differences. These results are evidence that the WM index is useful for forecasting.
For the NATSTAT index, again the trend specification dominates. Now, however, there is no evidence in favour of the leading index. A simple AR model, estimated with a trend, has forecasts superior to the bivariate model that includes the NATSTAT leading index. For the ABS index, the findings are slightly more favourable but only marginally so. The VAR model with trend provides only a three per cent improvement upon the simple AR model.
To summarise, there is evidence that the WM index and, to a lesser extent, the ABS index provide useful information that can improve the quality of forecasts for GDP. This does not appear to be the case for the NATSTAT index. In addition, there is some evidence that forecasts based upon a linear trend in GDP are superior to those based upon the imposition of a unit root, at least within the VAR framework and forecasting sample period we are considering.
For the monthly activity series, employment and unemployment, we consider only the WM index and the NATSTAT index (the ABS index is not available monthly). For the WM index and employment, we consider a VAR model in log-differences and in log-levels with a trend. For the NATSTAT index and employment, we consider the same models except that the index always enters as a logarithm of the published series and is not otherwise transformed. The results for these models are reported in Table 4. We again report the RMSE statistics for the lag specification that provides the best forecasts at longer horizons.
| RMSE for forecast sample: 1990:M1–1999:M4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecast horizon (months) | |||||||||
| p | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| WM (1966:M7–1999:M4) | |||||||||
| Differenced | 14 | 0.0053 | 0.0081 | 0.0118 | 0.0160 | 0.0197 | 0.0235 | 0.0269 | 0.0301 |
| Trend | 1 | 0.0059 | 0.0094 | 0.0127 | 0.0155 | 0.0175 | 0.0186 | 0.0188 | 0.0185 |
| Naïve (differenced) | 6 | 0.0057 | 0.0093 | 0.0138 | 0.0186 | 0.0224 | 0.0259 | 0.0289 | 0.0320 |
| Naïve (trend) | 10 | 0.0053 | 0.0080 | 0.0111 | 0.0144 | 0.0163 | 0.0178 | 0.0186 | 0.0197 |
| NATSTAT (1966:M12–1999:M4) | |||||||||
| Differenced | 2 | 0.0056 | 0.0090 | 0.0134 | 0.0178 | 0.0217 | 0.0251 | 0.0280 | 0.0307 |
| Trend | 16 | 0.0053 | 0.0076 | 0.0109 | 0.0143 | 0.0169 | 0.0192 | 0.0206 | 0.0223 |
| Naïve (differenced) | 6 | 0.0057 | 0.0093 | 0.0138 | 0.0186 | 0.0224 | 0.0259 | 0.0289 | 0.0320 |
| Naïve (trend) | 10 | 0.0053 | 0.0080 | 0.0111 | 0.0144 | 0.0163 | 0.0177 | 0.0185 | 0.0196 |
| No change (growth) | – | 0.0137 | 0.0251 | 0.0374 | 0.0507 | 0.0640 | 0.0767 | 0.0894 | 0.1042 |
|
Notes: The lag length is p and is chosen to minimise the RMSE for our forecast sample at the 24-month horizon. All RMSE statistics are in terms of levels of the activity series. For the NATSTAT differenced model, only the activity variable is in differences. The naïve model is an AR(p) model in the activity variable, either in differences or in levels with a trend. |
|||||||||
As with the GDP models, the specifications that include a linear trend dominate those that do not. For employment and the WM index, the RMSE statistics at the three, twelve and twenty-four month horizons are approximately 0.6, 1.6 and 1.9 per cent (trend specification). These can be compared with the average three, twelve and twenty-four month ended absolute growth rates for employment to gauge the magnitude of the prediction error. For 1990:M1–1999:M4, these growth rates are 0.6, 1.9, and 3.6 per cent. These errors are relatively large although again the relative magnitude is less at longer horizons.
As before, we can compare the RMSE statistics from the VAR model with index to those from a simple AR(p) model for employment to gauge whether or not the index contributes to forecasting performance. For both indices, when we consider the models in differences, there is a gain from including the index, particularly at longer horizons. The forecasts for the differenced models, however, are quite poor and in both cases are dominated by models with trend. For the models with trend, however, there is no evidence of any gain in forecasting performance. Although not uniform across all forecast horizons, generally the simple AR(p) model with trend performs at least as well as the VAR models. From this we conclude that neither index contributes to forecasts of employment.
For the WM index and unemployment, we consider VAR models in differences and in levels. We do not consider a simple linear trend since this is unlikely to provide a reasonable representation of unemployment. For the NATSTAT index and unemployment, we consider a VAR with unemployment in differences. These results are reported in Table 5.
| RMSE for forecast sample: 1990:M1–1999:M4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecast horizon (months) | |||||||||
| p | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
|
Notes: The lag length is p and is chosen to minimise the RMSE for our forecast sample at the 24-month horizon. All RMSE statistics are in terms of levels of the activity series. For the NATSTAT differenced model, only the activity variable is in differences. The naïve model is an AR(p) model in the activity variable, either in differences or in levels. |
|||||||||
| WM (1959:M9–1999:M4) | |||||||||
| Differenced | 8 | 0.0029 | 0.0049 | 0.0075 | 0.0103 | 0.0130 | 0.0151 | 0.0172 | 0.0190 |
| Levels | 12 | 0.0030 | 0.0050 | 0.0075 | 0.0103 | 0.0130 | 0.0154 | 0.0178 | 0.0200 |
| Naïve (differenced) | 5 | 0.0032 | 0.0052 | 0.0079 | 0.0104 | 0.0127 | 0.0149 | 0.0170 | 0.0189 |
| Naïve (levels) | 6 | 0.0032 | 0.0052 | 0.0078 | 0.0102 | 0.0124 | 0.0143 | 0.0161 | 0.0176 |
| NATSTAT (1966:M12–1999:M4) | |||||||||
| Differenced | 5 | 0.0031 | 0.0051 | 0.0079 | 0.0106 | 0.0132 | 0.0156 | 0.0179 | 0.0200 |
| Naïve (differenced) | 5 | 0.0031 | 0.0052 | 0.0078 | 0.0104 | 0.0128 | 0.0151 | 0.0173 | 0.0194 |
| No change (level) | – | 0.0039 | 0.0069 | 0.0099 | 0.0126 | 0.0150 | 0.0168 | 0.0185 | 0.0198 |
For both the WM index and the NATSTAT index, there is little to choose between any of the models. The magnitude of these errors can again be put into some perspective by comparing them to observed absolute changes in unemployment over the forecast sample. For 1990:M1–1999:M4, the average of the absolute value of the three, twelve, and twenty-four month ended changes are 0.3, 0.9, and 1.7 per cent. These are roughly the same magnitude as the RMSE statistics themselves indicating that the forecasts are fairly unreliable. In terms of the contribution, here again we find relatively little evidence in favour of either index. At all horizons, both the single variable model and the VAR models with index perform roughly the same. In fact, a simple no change forecast (in the level of unemployment) also has RMSE statistics of similar magnitude.
Taken together, the results of Tables 3–5 suggest that the WM index provides some additional information for forecasting GDP while the other two indices do not. For employment and unemployment, there does not appear to be any role for using any of the three indices for forecasting. These conclusions are subject, however, to some qualifications. First, we are considering only forecasting performance in terms of the RMSE of the level of the variables being forecasted. Second, our results are for a particular forecasting sample, 1990–1999. This sample is chosen because it is of a reasonable length and it encompasses most phases of the business cycle. While we have some evidence that the broad thrust of these conclusions is robust to a different sample period (discussed in the following section), nonetheless they may be sensitive to alternative samples. Finally, we have chosen to evaluate these indices in terms of simple two variable VAR models. We fully recognise that there are likely to be superior forecasting models. Our results, however, suggest that the leading indices can only play a limited role in these models.
3.3.2 Comparison to Gruen and Shuetrim (1994)
The next issue is to consider how well these results compare with a structural model for GDP. The model we consider is a version of the output equation presented in Gruen and Shuetrim (1994). This model has proved to be reasonably useful for forecasting purposes and is a reasonable basis for comparison.
Full details of the model and the estimation are presented in Appendix D. For purposes of discussion, we need only note that the Gruen and Shuetrim (GS) model is a single equation error correction model, with a long-run equilibrium relationship between domestic GDP and US GDP. The model also includes a measure of real interest rates and the Southern Oscillation Index (SOI). The latter is a weather variable and is designed to capture the influence of agriculture on Australian GDP. Full details of the variables are in Appendix A. For forecasting purposes, we have a number of variables which are exogenous to the model and which require some form of forecast themselves. We proceed as follows. We assume that the real interest rate and the SOI are unchanged from the final quarter of the sample used for the forecast. For US GDP, we consider two possibilities. The first is to use actual US GDP values, referred to as GS (actual US); the second is to use Consensus forecasts of the correct vintage, referred to as GS (Consensus US). We consider the first because we wish to understand how the quality of domestic GDP forecasts depends upon the quality of US GDP forecasts. The second roughly approximates a real time forecasting exercise, at least with respect to US GDP.
For purposes of comparison, we consider only the WM index. This simplifies the exposition and can be justified by its better out of sample performance compared with the other two indices. We also consider two forecasting sample periods, 1990:Q1–1999:Q1 and 1994:Q1–1999:Q1. Ideally, we would like to consider a sample of reasonable length and one that encompasses both upturns and downturns of the business cycle. The 1990:Q1–1999:Q1 sample satisfies this requirement. In addition, we are able to obtain correct vintage Consensus Forecasts for US GDP for this period. An evaluation of out of sample forecasting performance has other requirements, however, that makes this sample less than ideal. The forecasting sample period should not include any part of the sample for which a model has been specified. The Gruen and Shuetrim equation is specified for a sample 1980:Q1–1993:Q4 and properly we should consider forecasting sample periods subsequent to this. For this reason, we consider the 1994:Q1–1999:Q1 sample to allow us to approximate more closely a real time forecasting exercise.[17]
Table 6 presents the results for comparison. For the 1990:Q1–1999:Q1 period, we present the RMSE statistics for two VAR models using the WM index and GDP. Both models include a trend; the first has two lags and the second has eight lags. The choice of the trend specification reflects its superior performance identified previously. Similarly, we consider the model with lag length two as it is the model with the best forecasting performance at long horizons. Knowledge that a trend specification and lag length of two is superior to other specifications, however, is based upon information not available within sample. With respect to the trend specification, it seems reasonable to consider this as a candidate model. With respect to lag length, however, it is likely that a longer lag length would be chosen based upon within sample criteria. For simplicity, we consider a lag length of eight.
| Comparison with Gruen and Shuetrim (1994) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecast sample: 1990:Q1–1999:Q1 | |||||||||
| Model | Forecast horizon (quarters) | ||||||||
| p | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| VAR (trend) | 2 | 0.0075 | 0.0112 | 0.0150 | 0.0183 | 0.0212 | 0.0238 | 0.0258 | 0.0272 |
| VAR (trend) | 8 | 0.0095 | 0.0141 | 0.0175 | 0.0208 | 0.0247 | 0.0273 | 0.0298 | 0.0322 |
| GS (actual US) | – | 0.0068 | 0.0085 | 0.0104 | 0.0122 | 0.0131 | 0.0133 | 0.0136 | 0.0144 |
| GS (Consensus US) | – | 0.0075 | 0.0101 | 0.0133 | 0.0165 | 0.0194 | 0.0214 | 0.0227 | 0.0245 |
| Forecast sample: 1994:Q1–1999:Q1 | |||||||||
| Forecast horizon (quarters) | |||||||||
| Model | p | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| VECM | 2 | 0.0064 | 0.0081 | 0.0091 | 0.0094 | 0.0081 | 0.0081 | 0.0098 | 0.0099 |
| VECM | 8 | 0.0079 | 0.0109 | 0.0127 | 0.0146 | 0.0166 | 0.0189 | 0.0223 | 0.0254 |
| GS (actual US) | – | 0.0068 | 0.0071 | 0.0092 | 0.0101 | 0.0100 | 0.0105 | 0.0106 | 0.0095 |
| GS (Consensus US) | – | 0.0067 | 0.0075 | 0.0103 | 0.0124 | 0.0138 | 0.0165 | 0.0192 | 0.0213 |
|
Notes: The lag length is p. All RMSE statistics are in terms of the level of GDP. The VAR (trend) and the VECM model are bivariate models using GDP and the WM index. For these models estimation starts in 1960:Q1. GS refers to the Gruen and Shuetrim (1994) model, described in Appendix D. GS (actual US) uses actual US GDP for the forecast period. GS (Consensus US) uses Consensus forecasts for US GDP. The other explanatory variables in the GS equation are assumed unchanged for the forecast period. Estimation for the GS models starts in 1980:Q1. See Appendix D for further details. |
|||||||||
At all forecast horizons, the GS model using either actual values or consensus forecasts of US GDP for forecasting outperforms the VAR models. And it does so by a reasonable amount, especially at longer horizons. This suggests that the VAR models using the WM index can be improved upon, although the full extent remains unclear because of the fact that the GS model is specified over part of the forecasting sample period. When we compare the RMSE of forecasts from the GS model using actual values to those using consensus forecasts of US GDP, not surprisingly, we obtain significantly better forecasts using actual future values of US GDP. This is also the case for the later forecast sample starting in 1994. So, in a framework that relies upon US GDP for forecasting, such as the GS model, the quality of the forecasts for Australian GDP will always be limited by the quality of forecasts for US GDP.
The results for the later forecasting sample period are also reported in Table 6. In this case, we consider a VECM model using the WM index because, for this forecasting sample period, it outperforms other models. (The improvement is not too large. For the WM index VAR model with trend, the RMSE statistic at the eight-quarter horizon is 0.0111. A full set of results is available from the authors.) As is evident from Table 6, for the VECM model the choice of lag length is very important. If we choose a lag length of two, we obtain very high quality forecasts (judged over this sample). If we choose a lag length of eight, which is quite likely based upon within sample evaluation, we obtain quite poor forecasts. And the comparison to the performance of GS (Consensus US) depends upon this choice. With a small number of lags, the VECM significantly outperforms the GS (Consensus US); with a larger number of lags, the opposite is true.
The comparison to Gruen and Shuetrim (1994) suggests that there are more accurate means to forecast real GDP than simple time series models of an activity variable and a leading index. Nonetheless, the out of sample results provide some evidence that the WM leading index can provide useful information for forecasting, even within simple forecasting models. Certainly, if one was careful about specification and took on board the evidence in favour of parsimonious models (both from our results and the forecasting literature), then one should be able to obtain forecasts of reasonable quality.[18]
Footnotes
Trevor and Donald (1986) also use quarterly averages of the indices they consider. By the end of a quarter we have the WM index for that quarter's first month. Our results do not exploit this slight informational advantage as we found that there was very little gain in doing so. [7]
In principle, it is possible to exploit the additional information we have concerning employment and unemployment, see Robertson and Tallman (1999). [8]
The conclusions we present are not sensitive to alternative lag lengths. [9]
For example, it is well recognised that Bayesian VAR models outperform unrestricted VAR models in terms of forecast quality. See the discussion in Robertson and Tallman (1999). Alternatively, Clements and Hendry (1999) argue for intercept correction in forecasting models as a means of improving forecast quality. [10]
This is the standard measure used in the forecasting literature to evaluate the quality of forecasts and, as a criterion for model selection, can be justified by a desire to minimize the average prediction error of a model. There are other alternatives. For example, we may wish to use criteria that measure the ability of the model to forecast turning points, as is common in much of the leading indicator literature. See, for example, the discussion in Granger (1989). [11]
Simply, the VEC model imposes a single cointegrating restriction between the leading index and the activity variable. See Hamilton (1994, ch 19) for a more detailed discussion. [12]
Generally speaking, the specification that performs best at the longer horizons performs relatively well at shorter horizons. There are, however, situations where this is not the case. Nonetheless, the conclusions we present are not critically dependent upon this. Note also that in some situations, the choice of lag length can be ambiguous. In such cases, we use performance at shorter horizons as our guide. A full set of results is available from the authors. [13]
Approximately, since we are in logarithms. [14]
Here are the relationships discussed in the text in more detail. For the one-step ahead
log-level forecast, the prediction error is decomposed as: 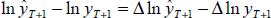 .
For the four-step ahead forecast, the prediction error is decomposed as:
.
For the four-step ahead forecast, the prediction error is decomposed as: 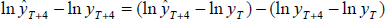 .
The prediction error for the eight-step ahead forecast can be decomposed in a similar
fashion. Since the RMSE statistics are in absolute terms, for comparison we consider the
absolute value of the quarterly growth rates when averaging.
[15]
.
The prediction error for the eight-step ahead forecast can be decomposed in a similar
fashion. Since the RMSE statistics are in absolute terms, for comparison we consider the
absolute value of the quarterly growth rates when averaging.
[15]
We can also compare the RMSE to a simple no change forecast, in this case no change in
the growth of GDP: 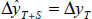 . This is a standard assessment in the
forecasting literature and the RMSE statistics for a no change forecast are reported in
the tables. For GDP and for employment, a no change forecast is particularly poor and
merits little discussion. We will consider the comparison when we consider unemployment.
[16]
. This is a standard assessment in the
forecasting literature and the RMSE statistics for a no change forecast are reported in
the tables. For GDP and for employment, a no change forecast is particularly poor and
merits little discussion. We will consider the comparison when we consider unemployment.
[16]
Comparing the two forecasting samples gives us an idea of the sensitivity of our results to the data used. Our results may also be sensitive to the estimation sample. Throughout this paper we have used all available data to estimate the models. An alternative would be to use the same estimation sample, as well as forecast sample, when comparing forecasts from various models. To see if this affects our conclusions, we examine the forecasting ability of the VAR models using the same sample period as used for the GS model, estimating from 1980 and forecasting from 1990, and the results are much the same as those reported in Table 6. These results are available from the authors on request. We thank Mardi Dungey for raising this issue. [17]
One could also consider the techniques designed to improve forecasts discussed in Clements and Hendry (1999). Further, one could consider forecast pooling procedures from these simple VAR models. See Granger and Newbold (1986) for a discussion of this and Stock and Watson (1998) for a practical application. [18]