RDP 1999-03: Householders' Inflation Expectations 2. The Distribution of Householders' Inflation Expectations
January 1999
- Download the Paper 390KB
2.1 The Data
2.1.1 The Melbourne Institute survey of householders
This paper uses unit record data from the Melbourne Institute of Applied Economic and Social Research Surveys of Consumers, hereafter referred to as ‘the survey’. While the survey started on a quarterly basis in March 1973, it shifted to a monthly basis in December 1986. It is a stratified random sample of 1,200 respondents,[1] and is conducted in the first half of the month. Respondents are asked a range of questions, including what they expect inflation, unemployment, wages growth and national financial conditions to be over the coming year. Since January 1995, respondents have also been asked detailed questions about their personal characteristics, including gender, age, education, income, location, voting preference, type of home ownership and, periodically, whether their wage is determined by an award, enterprise agreement or other method. Data at this disaggregated level allow a more detailed examination of the behaviour and determinants of inflation expectations. Appendix A sets out certain sections of the questionnaire used by interviewers.
Given that a different group of respondents is interviewed each month, unit record analysis is restricted to cross-section techniques, since there is no time dimension in responses. Median inflation expectations, however, are amenable to time-series analysis because this statistic is available through time.
The Melbourne Institute makes some adjustments to the raw data in estimating the median value of expected inflation. The first is to convert qualitative responses into quantitative ones. People are asked what they expect inflation to be in the following way: ‘By this time next year, do you think the prices of the things you buy will go up or down? If up, by how much? If down, by how much?’.[2] About 15 to 20 per cent of respondents decline to nominate an actual figure. These qualitative responses are converted to a quantitative form by allocating them according to the distribution of quantitative responses in the same direction in that month, or if there were none, according to the average distribution of the closest months in which there were quantitative responses. While this allocation of qualitative responses requires the assumption that qualitative responses are distributed in the same way as quantitative responses, the adjustment has only a marginal impact on the calculated median inflation expectation.
The second adjustment is to align the survey responses with the relevant census data for gender, age and location in an attempt to correct for possible sampling bias. This reduces sampling variability in the estimate of the median. In this paper, the median measure is adjusted in both of these ways. When we use the unit record data, however, the responses are not subject to either of these adjustments. Statistical analysis of the individual responses is only based on quantitative answers, and these responses are not re-weighted by the census data since the Melbourne Institute's weights are based on all responses, not just the quantitative responses.
2.1.2 Problems with survey and unit record data
While surveys can be a rich source of economic information, there are a number of commonly identified problems with using survey data. The first is sampling error (Berk 1997), although some correction is made for this in the analysis of median expected inflation by weighting responses according to census data to obtain a more accurate representation of the population. A further problem is that survey responses can be sensitive to the order and construction of questions. There is, for example, no systematic relation between what householders expect to happen to prices and their wages over the coming year. This result is discussed in Section 4.1.2.
Survey data on expectations may also be unreliable if respondents lack an incentive to report the truth. Moreover, even if they do report what they believe, they may not act on this. Englander and Stone (1989), however, provide evidence for the United States that survey responses are sufficiently acted upon to make their collection useful.
But, more fundamentally, there can also be respondents who provide extreme and what are, on the face of it at least, unreasonable answers to questions in a survey. For example, respondents can indicate numbers for expected inflation which are well out of the bounds of experience, such as saying that inflation will be 50 per cent or 100 per cent over the coming year. One way to deal with this problem is simply to accept that it is what people genuinely think and perform the analysis accordingly. Another way is to limit the influence of extreme observations. The most common method of doing this is to use the median or middle observation, rather than the mean. The median is affected by the number of responses either side of it, but not by their actual values. An imbalance in the number of negative and positive extreme responses, however, implies that extreme responses affect the median inflation expectation.
Another way of dealing with extreme responses is to use trimmed statistics which are calculated by arbitrarily, and not necessarily symmetrically, imposing zero weights on proportions of observations at each end of the distribution. This is, for example, a standard method of estimating underlying inflation (Roger 1997; Kearns 1998). We deal with extreme observations by truncating the distribution to those inflation expectations lying between 0 and 10 per cent. This is arbitrary but it roughly spans the range of inflation experience over the past 15 years, during which underlying inflation has ranged from 1.4 per cent to 9.9 per cent and headline inflation has ranged from −0.3 per cent to 11.1 per cent. This truncation preserves some features of the distribution, such as positive skewness and fat tails, but in a considerably moderated form.
2.2 General Features of Householders’ Inflation Expectations
McDonnell (1994) provides a descriptive discussion of the Melbourne Institute survey from 1973 to 1994. Figure 1 shows householders' measured inflation expectations along with headline and underlying inflation from 1976 (which is when the Melbourne Institute started publishing the median). While expectations were fairly inflexible in the second half of the 1970s and in the 1980s, they did respond to the introduction of Medicare in 1984 (McDonnell 1994). Average expected inflation fell in line with the reduction in inflation in the early 1990s, but more slowly than underlying inflation, de Brouwer and Ellis (1998) used Granger-causality tests to show that there is feedback between expected and actual inflation. They also report that this measure of expected inflation moves one-for-one with inflation, but has been 2 per cent higher than inflation on average from 1980 to 1997. An explanation for this positive bias in inflation expectations compared with measured inflation is that people are not making the quality adjustments to their estimates of price changes that are made when calculating published inflation measures, although this alone is unlikely to explain the degree of bias observed in inflation expectations.
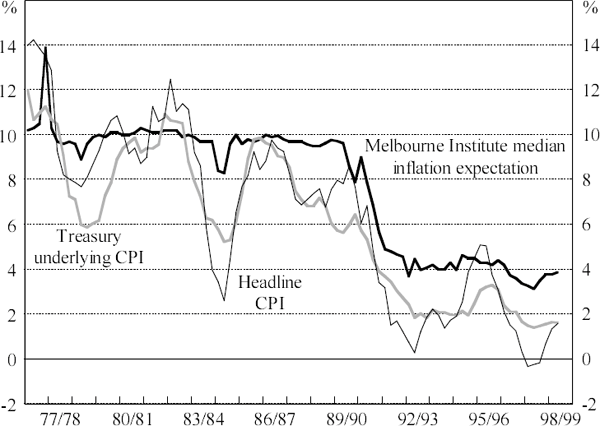
McDonnell also reports that the proportion of quantitative responses has increased substantially over time. The proportion of respondents who say that prices will rise, but do not specify by how much, has fallen from about 35 per cent in the mid 1970s to about 20 per cent in the mid 1990s. This is now closer to 15 per cent. McDonnell attributes this to improvements in communications, information and education. Alternatively, inflation uncertainty may have been considerably higher in the 1970s because of the substantial price shocks in that decade.
Another feature of the Melbourne Institute inflation expectations series is that responses cluster around key round numbers like 0, 2, 3, 5 and 10, the usual explanation for which is that people nominate round (often decimal) numbers when they are uncertain (Harris and Harding 1998a). The relative preponderance of the numbers 2 and 3 in the past few years is consistent with price movements in recent years and with the Reserve Bank's inflation target of 2 to 3 per cent, on average, over the medium term.
Figure 2 shows the relative frequency distribution of responses for four periods from 1995 to 1998. About 10 per cent of respondents expect no inflation, and around 30 per cent of respondents expect inflation to be 2 or 3 per cent. Approximately a quarter of respondents expect inflation to be 5 per cent, and 10 per cent expect inflation to be 10 per cent. About 10 per cent of respondents expect inflation in excess of 10 per cent, again with round-number decimal clustering at 15, 20, 25 and 50 per cent, and a very small percentage of respondents expect deflation. Over the past four years, consistent with actual inflation outcomes, the distribution of expectations has shifted downwards, with about 15 per cent of respondents expecting no change in prices in January 1998.
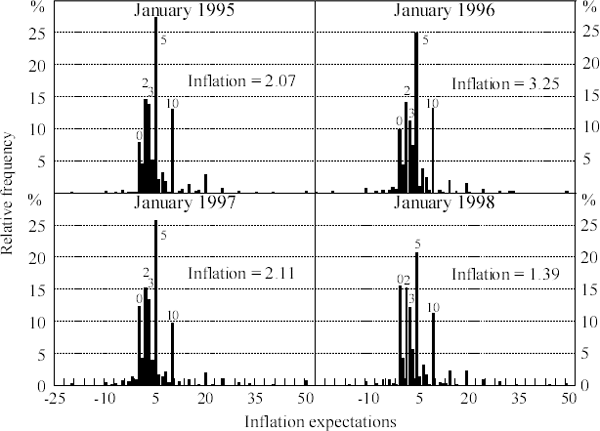
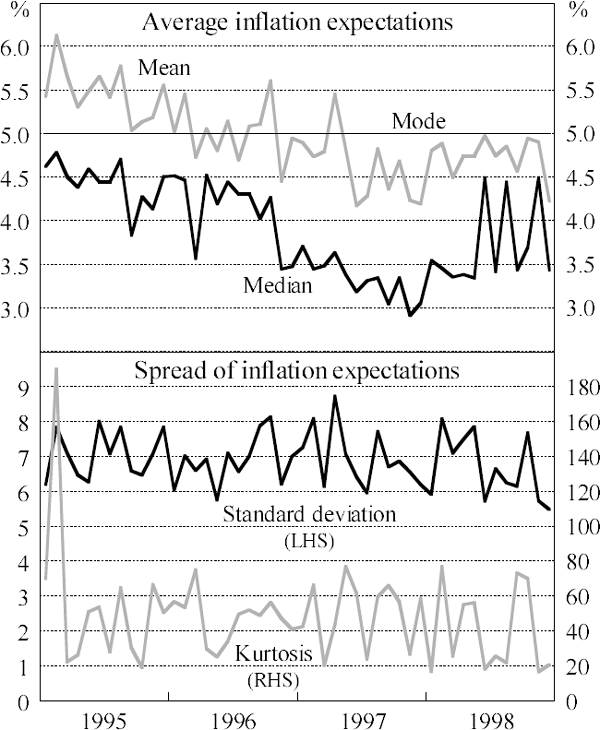
It is clear from Figure 2 that householders' inflation expectations are not normally distributed. The distributions are all skewed to the right and fat tailed, reflecting the relatively high number of people who expect very high inflation over the coming year. Table 1 provides some descriptive statistics for the period January 1995 to December 1998. The statistics are provided for the full sample and for the subgroup of respondents who expect inflation to be between 0 and 10 per cent, which is about 90 per cent of all respondents. The median is lower than the mean of the distribution, although this is less pronounced when the distribution is truncated to exclude extreme observations. In 1990 the full sample mode shifted down from 10 per cent, which it had been since 1973, to 5 per cent, at which it still remains. Figure 3 shows how these statistics have evolved over time for the full sample. While both the mean and median of inflation expectations have fallen over time, there has been no substantial change in the mode, standard deviation or kurtosis. This indicates that the distribution of inflation expectations has shifted to the left in response to lower inflation, but the shape of the distribution remains essentially the same.
| All respondents |
Respondents who expect 0–10 per cent inflation |
|
|---|---|---|
| Median | 3.90 | 3.70 |
| Mean | 4.97 | 4.03 |
| Mode | 5.00 | 5.00 |
| Standard deviation | 6.91 | 2.91 |
| Skewness coefficient | 4.45 | 0.67 |
| Kurtosis coefficient | 48.79 | 2.80 |
|
Note: Statistics are the monthly average from January 1995 to December 1998. |
||
Footnotes
Only about one-quarter of the people contacted agree to be interviewed, so the actual number of people contacted each month is closer to 5,000. [1]
Respondents who think prices will go down have only been asked to nominate a specific figure since June 1992. Publication of these quantitative responses in the Melbourne Institute's report on inflation expectations commenced in 1993, but has since ceased. [2]