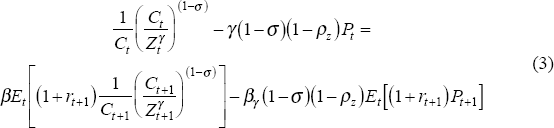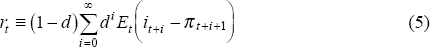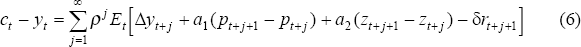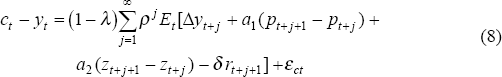RDP 9812: An Optimising Model for Monetary Policy Analysis: Can Habit Formation Help? 3. A Simple Habit Formation Model
September 1998
- Download the Paper 395KB
Following Carroll, Overland and Weil (1995), consumers' t-period utility may be expressed as:
where Zt is the habit-formation reference consumption level, defined as:
Note that utility is no longer time-separable, because the consumption choice today influences the future habit reference level in next period's and all future periods' utility. One advantage of this simple habit formation specification is that it conveniently parameterises two features of habit formation:
- The parameter γ indexes the importance of habit formation in the utility function. If γ = 0, then the standard model applies. If γ = 1, then only consumption relative to previous consumption matters. γ > 1 is not admissible, because it implies that steady-state utility is falling in consumption.
- The parameter ρz indexes the persistence or ‘memory’ in the habit formation reference level. If ρz = 0, then only last period's consumption is important. For 0 < ρz ≤ 1, the larger is ρz, the further back in time is the reference level determined (or, more accurately, the longer is the ‘mean lag’ of the habit reference level).
Employing a standard budget constraint with time-varying interest rate, one can express the (nonlinear) first-order conditions for the consumer's problem as:
where Zt is defined above and Pt is defined as:
The ex ante real interest rate is defined as the discounted weighted average of model-consistent forecasts of short-term real interest rates, it − πt+1, or
where 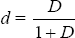 , and
D is the duration of the (implied) long-term real bond, which is set to 10 years for
this paper. The parameter ρ is the discount rate for future income (as
distinguished from the real interest rate; see Campbell and Mankiw (1991)), and thus indexes the
extent to which consumers look forward. (See Appendix A for a full
derivation of the first-order conditions and the linear approximations used below.)
, and
D is the duration of the (implied) long-term real bond, which is set to 10 years for
this paper. The parameter ρ is the discount rate for future income (as
distinguished from the real interest rate; see Campbell and Mankiw (1991)), and thus indexes the
extent to which consumers look forward. (See Appendix A for a full
derivation of the first-order conditions and the linear approximations used below.)
3.1 A Linearised Consumption Function
In order to derive an explicit consumption function, I linearise the first-order conditions and substitute into the linearised budget constraint, obtaining the approximate log-linear consumption function (see Appendix A for details):
with Pt defined as:
where lower-case letters denote logarithms, and the parameters a1, a2, and δ are nonlinear functions of the underlying parameters γ, σ, ρz, β, and I impose these nonlinear constraints on the parameters.[4]
Campbell and Mankiw (1989, 1990, 1991) provide compelling evidence for the existence of rule-of-thumb consumers, i.e. consumers whose current consumption equals current income. This constitutes a strong violation of the permanent income theory, because a significant fraction of this period's income is predictable as of last period. A permanent income consumer would consume beginning in last period the annuity value of the component of current income that was predictable last period. I allow for the possibility of rule-of-thumb consumers in the log-linear consumption function by modifying it as:
where λ represents the fraction of total income accruing to rule-of-thumb consumers (who follow the rule ct = yt), and εct is the structural innovation in the consumption equation, usually interpreted as the innovation to lifetime resources.
Thus specified, the model nests a number of interesting alternatives, including: the standard PIH model (λ = 0, γ = 0), the PIH with some rule-of-thumbers (γ = 0), a forward-looking habit formation model (γ ≠ 0), as well as other combinations. In addition, the parameter ρ, which is the discount factor applied to future income and the future marginal effects of current consumption decisions through habit formation, indexes the degree of forward-lookingness in the model.
3.2 Estimating and Testing the Consumption Function
To estimate the underlying parameters, I employ a numerical maximum likelihood method which is documented in Fuhrer and Moore (1995a). The advantages of this system approach are that; (1) it allows estimation to proceed naturally from an unrestricted linear vector autoregression that nests all of the linear models considered to successively more-restricted linear models, with each succeeding restriction nested within the preceding less-restricted model and within the VAR; and (2) the finite sample properties of the estimator may be more desirable than method-of-moments estimators, as documented in Fuhrer, Moore and Schuh (1995), and West and Wilcox (1993). A drawback to the approach is that, to the extent that any equation in the system is mis-specified, estimates of all the parameters in the system will (in principle) be affected. However, I pursue an estimation strategy below that is designed to minimise the exposure to this risk.
The ultimate goal of this paper will be to embed the estimated consumption function in a monetary policy model with sticky prices and sticky inflation, in order to determine to what extent the modifications to consumption entertained here alleviate the problems identified in earlier work. Thus, I begin with an unconstrained vector autoregression that includes the minimum set of variables necessary to nest the final monetary policy model. These are log per capita nondurables and services consumption, log per capita disposable personal income, the federal funds rate, the price level, and log per capita GDP other than nondurables and services consumption. Their definitions are provided in Table 1.
| Variable | Definition |
|---|---|
| Consumption | Chain-weighted expenditures on nondurables and services, per capita, detrended, trend segmented in 1974 |
| Income | Chain-weighted personal disposable income per capita, detrended as above |
| Short-term interest rate | Quarterly average of the effective federal funds rate |
| Prices | Consumer price index, excluding food and energy |
| Non-consumption GDP | Chain-weighted per capita GDP, excluding nondurables and services consumption, detrended as above |
In the first stage of estimation, I estimate only the parameters of the log-linear consumption function. The processes for income, the funds rate, prices and other GDP are unconstrained equations from the VAR. The definitions of zt, pt, and ex ante real rates rt are as above.
Footnote
In particular, the coefficients are defined as:
a1 = ((γ * (1 − σ) * (1 −
ρ)) / σ)
a2 = ((1 − σ) *
γ) / σ
δ = β
[(−γ(1 − σ) (1 −
ρz) − 1) / σ]
b1 =
(ρ − σ) / (1 − σ)
b2 =
(γ * (1 − σ) − 1) * (1 − σ)