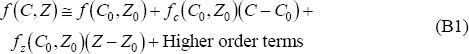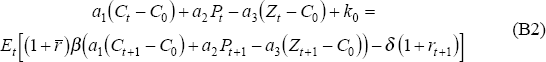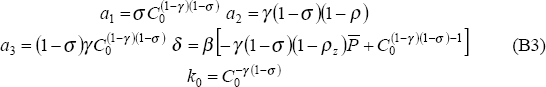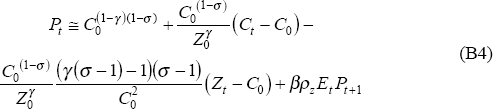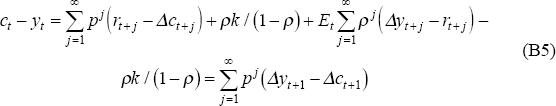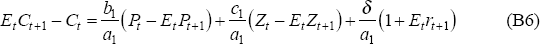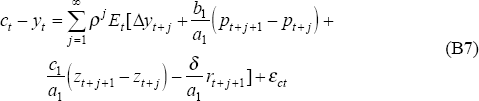RDP 9812: An Optimising Model for Monetary Policy Analysis: Can Habit Formation Help? Appendix B: Deriving an Approximate Linear Consumption Function

We approximate the first-order condition with its linear approximation about the steady-state values for C and Z:

In the steady state, Z = C, simplifying the linearised first-order condition, and we obtain:

where the coefficients a₁ and δ are defined as:

We approximate the summation defined in P_t as:

Utilising the approximation in Campbell and Mankiw (1991), we can write the log-linearised budget constraint in consumption and income as:

where lower-case letters denotes logs.

If we use the approximation 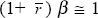in the Euler equation, then the expected change in consumption is:

Using the approximation that the changes in the level of C will be proportional to log changes in C (for a non-trending series – consumption is defined as per capita, less a segmented linear trend), and substituting this expression into the budget constraint, yields the approximate log-linear consumption function:

The parameters a₁, a₂, δ in Equation (6) correspond to b₁/a₁, C₁/a₁, and δ/a₁; the steady-state values for C₀ (and hence Z₀) are set arbitrarily to unity, and the steady-state value for P is determined accordingly. In the estimation step, I estimate δ as a parameter, not imposing all of the restrictions implied by the Euler equation. The final consumption function used in the empirical work is this equation with the addition of a fraction of income λ accruing to rule-of-thumb consumers.