RDP 9810: The Distribution and Measurement of Inflation 2. Behaviour of Price Changes
September 1998
- Download the Paper 326KB
In this section, the distribution of price changes is examined. An understanding of the manner in which prices change can deliver an important insight into the inflation process and the behaviour of measures of inflation. Further, it can assist in determining the best method for measuring core inflation. The distribution of quarterly price changes is examined, rather than changes over a longer horizon, as monitoring inflation over a shorter horizon provides more timely information on turning points in the trend of aggregate inflation.[1]
2.1 The Data
Quarterly CPI expenditure class data – the finest level at which the Australian CPI is available – from September 1980 until March 1998 are used in this study. At this level of disaggregation there are approximately 100 components, although with the introduction of new CPI series, weights are updated and components are occasionally added to, or removed from, the CPI.[2] In this paper, two components, mortgage interest charges and consumer credit charges, are excluded from the analysis from December 1986. Interest rates represent the cost of intertemporal consumption smoothing, and so are not a current price of a good or service. It is, therefore, preferable to exclude them from a measure of goods and services price inflation (RBA 1997). Indeed, following the most recent review of the CPI, the Australian Bureau of Statistics (ABS) will remove interest charges from the 13th series of the CPI to be introduced from September 1998 (ABS 1997b). For the remainder of this paper, ‘CPI’ and ‘total CPI’ will refer to the CPI excluding interest charges.
2.2 Defining the Distribution Moments
With many quarters of data, the moments of the distribution provide a useful summary of the distribution of component quarterly price changes. As shown in Appendix A, the aggregate quarterly inflation rate, πt, can be expressed as a weighted sum of the n component quarterly inflation rates, πit, where the time-varying weights, wit, are an amalgam of the series weights, the index levels, and splicing factors:
These time-varying weights are used in calculating the moments, 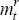 , of
the distribution of CPI component price changes. The first moment, where r = 1, the
mean rate of inflation, is defined by Equation (1). The higher-order, rth
central moment is defined as:
, of
the distribution of CPI component price changes. The first moment, where r = 1, the
mean rate of inflation, is defined by Equation (1). The higher-order, rth
central moment is defined as:
The second central moment, r = 2, the variance, and its square root, the standard deviation, σ, are measures of the dispersion of the distribution. The coefficients of skewness and kurtosis are scaled versions of the third and fourth moments:
These coefficients provide a summary of the shape of the distribution. For a symmetric distribution, the coefficient of skewness will be zero.[3] A positive coefficient of skewness indicates the distribution is skewed to the right, that is, the right-hand tail is longer than the left-hand tail. Conversely, a negative coefficient indicates that the distribution is skewed to the left. The kurtosis coefficient indicates the extent to which the distribution has fat tails (leptokurtosis, Kt > 3) or thin tails (platykurtosis, Kt < 3) relative to a normal distribution, which has a kurtosis coefficient of 3 (mesokurtosis). For the remainder of this paper, the term moments will be used somewhat loosely to refer to the mean, standard deviation and coefficients of skewness and kurtosis.
2.3 The Moments of Inflation
Figure 1 plots the moments of the distribution of CPI component price changes in each quarter. The top panel shows the mean price change in each quarter. The decline in the inflation rate is clearly seen with the mean price change smaller over the 1990s than over the 1980s. The periodic volatility of the mean is also apparent with several episodes where the mean inflation rate is significantly different in adjacent quarters.
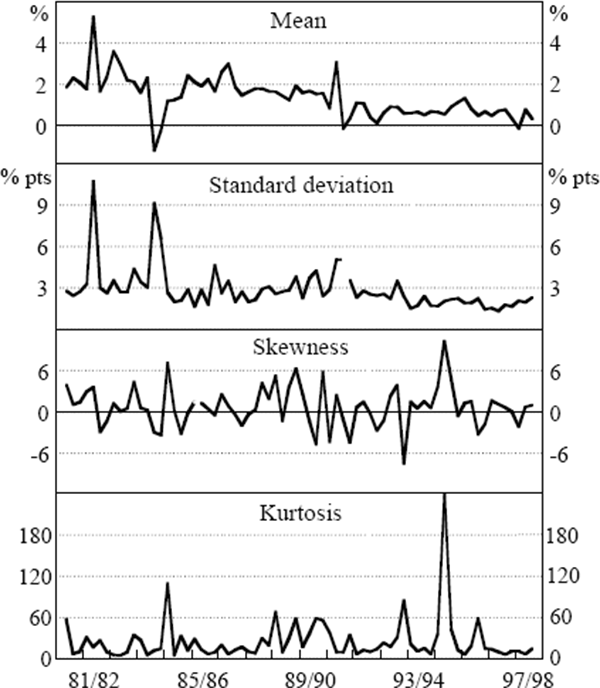
Several quarters of extreme mean price changes are worth noting. The large spike in inflation in December 1981 and the sharp fall in March 1984 were the result of movements in the cost of Hospital and Medical Services. Inflation picked up in late 1986 with the large depreciation in the exchange rate and the reversal of the oil price fall. Again in December 1990, at the time of the Gulf war, petrol prices caused a sharp rise in inflation, which was reversed in the subsequent quarter.
The large standard deviation demonstrates the significant dispersion of quarterly price changes. As shown in Appendix B, while some components are frequently in the tails, many components are occasionally in the tails.
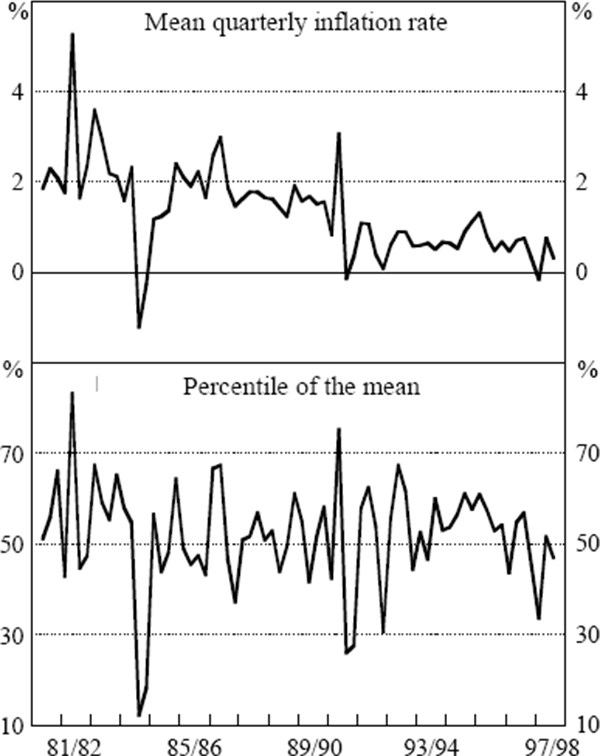
The plot of the coefficient of skewness in the third panel illustrates that in most quarters the distribution of price changes is skewed. The distribution is more often positively skewed than negatively skewed.[4] On average, the coefficient of skewness is 0.7, indicating that, typically, the right-hand tail of the distribution is longer than the left-hand tail. The coefficient of skewness is not the only measure of the distribution's asymmetry. An alternative simple diagnostic is to compare the mean and median of the distribution. If the distribution is symmetric, then the mean and median will be equal. However, Figure 2 demonstrates that the mean inflation rate usually has a percentile ranking greater than 50, indicating that the mean inflation rate is greater than the median inflation rate (so observations in the right-hand side of the distribution are, on average, further from the median than those in the left-hand side).[5] The percentile ranking of the mean also demonstrates that when the mean inflation rate moves sharply between quarters, it is typically some distance from the central portion of the distribution.
The kurtosis coefficient, as shown in Figure 1, is often very large. Indeed, it is greater than 3 in every quarter, indicating the distribution of quarterly price changes is always leptokurtotic (that is, more fat-tailed than a normal distribution). This indicates that in a typical quarter, a large proportion of the CPI basket experiences price changes significantly different from the mean inflation rate. Using the skewness and kurtosis coefficients, the normality of the distribution can be tested statistically. Not surprisingly, the null hypothesis, that the quarterly CPI component price changes have a normal distribution, can be comprehensively rejected in all but one quarter out of 70.[6]
The high import penetration of the Australian economy possibly contributes to the significant dispersion of price changes. A large appreciation or depreciation of the exchange rate will result in significant changes in the prices of imported goods, often placing largely imported CPI components in one of the tails of the distribution. This will skew the distribution, increasing its measured dispersion and the proportion of components in the tails. Over the sample period, the distribution of quarterly exchange rate changes is negatively skewed, suggesting asymmetric exchange rate shocks could be responsible for the positive skew of the distribution of price changes.[7] However, episodes of exchange rate depreciations, in particular the mid 1980s, do not coincide with increased positive skew of CPI component price changes.
An alternative explanation lies in the behaviour of the prices of non-market components, such as Government Dwelling Rents or Education. The prices of these components change infrequently, because of different pricing policy to the market sector, and possibly, as Roger (1995) suggests, because the non-market sector contains fewer price setters.
Table 1 demonstrates that the coefficient of skewness falls when the components whose prices are set, or heavily influenced by, government policy, are excluded.[8]
| Mean |
Standard deviation |
Skewness |
Kurtosis |
|
|---|---|---|---|---|
| September 1980 to March 1998 | ||||
| Original: | ||||
| All components | 1.35 | 2.87 | 0.69 | 24.97 |
| Excluding policy components(a) | 1.23 | 2.45 | 0.49 | 31.36 |
| Seasonally adjusted:(b) | ||||
| All components | 1.35 | 2.47 | 0.32 | 22.27 |
| Excluding policy components(a) | 1.23 | 2.06 | 0.41 | 29.32 |
| September 1990 to March 1998 | ||||
| Original: | ||||
| All components | 0.70 | 2.34 | 0.35 | 26.65 |
| Excluding policy components(a) | 0.52 | 2.06 | 0.20 | 37.66 |
Notes: (a) The CPI excluding policy components is the total CPI less
those components excluded from the Treasury underlying CPI basket because their
prices are heavily affected by changes in government policy, see footnote 8. |
||||
Non-market prices therefore clearly contribute to the skewness of price changes. Table 1 also presents evidence that there is a seasonal element to non-market prices. Seasonal adjustment reduces the coefficient of skewness more in the total basket than in the market basket, implying that skewness in non-market components contributes disproportionately to the skewness of price changes.[9]
Non-market components cannot, however, account for all of the skewness of price changes, since even the market basket exhibits substantial skewness. Seasonal adjustment of this basket has very little effect on skewness, suggesting that the remaining skewness does not derive from seasonal price changes.[10]
Given that the distribution's skew cannot solely be attributed to infrequent but systematic price adjustment, there is obviously a more fundamental cause. Two models that deliver a skewed distribution of price changes are proposed by Ball and Mankiw (1995) and Balke and Wynne (1996). In Ball and Mankiw's model, menu costs generate a positive relationship between the rate of inflation and the skewness of the distribution of price changes. De Abreu Lourenco and Gruen (1995) extend this model to show that the inflationary impetus of the dispersion of shocks depends on the level of inflation expectations. Balke and Wynne generate a skewed distribution of price changes that is positively related to the mean inflation rate, using a different framework. They use a dynamic equilibrium model with flexible prices, and show that if there is an asymmetric input-output relationship between sectors, the mean and skew of the distribution will be positively related. It is beyond the scope of this paper to investigate the fundamental cause of the skewness in the distribution of Australian consumer prices. Rather, its existence, and the extent to which it is caused by seasonality or is a sectoral phenomenon, is noted for the impact it has on the construction of a statistical measure of core inflation.
2.4 Correlations of the Moments
The correlations of the moments in Table 2 demonstrate that the dispersion of price changes is positively related to the mean rate of inflation. The finding that price changes are more dispersed at higher rates of inflation is consistent with a wide body of literature, which has been surveyed thoroughly by Golob (1993). There is little accord within this literature on the cause or nature of this relationship. Fischer (1981) lists a range of models that support a relationship between the rate of inflation and relative price variability. As Golob (1993) notes, the empirical evidence has supported models premised on sticky prices, menu costs, limited information and supply shocks. The differing models also have a range of implications for the causality between inflation and the dispersion of price changes and the economic costs of relative price variability. The mean rate of inflation is also found to be positively correlated with the skew of the distribution of price changes, a result that is consistent with the models by Ball and Mankiw, and Balke and Wynne discussed above.
| Mean | Standard deviation | Skew | Kurtosis | |
|---|---|---|---|---|
| Mean | 0.30 | 0.25 | −0.09 | |
| Standard deviation | 0.24 | −0.12 | −0.04 | |
| Skew | 0.27 | −0.07 | 0.38 | |
| Kurtosis | −0.12 | −0.05 | 0.41 | |
Notes: (a) The correlations in the lower triangle are for the moments of the full CPI basket from September 1980 to March 1998 while those in the upper triangle are from September 1990 to March 1998. |
||||
If a subset of components experienced extreme price changes, both the standard deviation and kurtosis coefficient would rise, so these moments would be positively correlated. No positive correlation, however, is found. Indeed, the standard deviation and kurtosis of the distribution are slightly negatively correlated. A significant negative correlation would suggest that increases in the standard deviation are associated with increased dispersion of the central core of the distribution rather than of outlying observations in the tails. In addition, the skew and kurtosis are positively related, implying that the fat-tails of the distribution are often not symmetric.
The nature of CPI component price changes will determine the behaviour of the CPI and any measure of core inflation which is based on the CPI components. Having examined the distribution of price changes, summarised by the moments and their correlations, Section 3 describes various methods for measuring core inflation and investigates the range of trimmed mean measures of core inflation.
Footnotes
There are also pragmatic reasons for examining quarterly changes. Since the CPI is spliced using quarterly changes when the weighting regime changes, it is not possible to express the aggregate inflation rate as a weighted sum of the component inflation rates for horizons longer than one quarter. The derivation of the quarterly inflation rate as a weighted sum of the component inflation rates is shown in Appendix A. [1]
Initially, there are 97 components, from March 1982 until September 1986 this increases to 102, and thereafter there are 107 components. [2]
Note, however, that skewness and asymmetry are not synonymous terms. Symmetry implies that the left and right sides of the distribution are mirror images, while the coefficient of skewness compares the density of the tails in distance relative with the mean. It is possible that a distribution may be asymmetric and yet have a zero coefficient of skewness. However, a distribution with a non-zero coefficient of skewness must be asymmetric. [3]
In 45 quarters the distribution is positively skewed, while it is negatively skewed in only 25. [4]
On average, the mean is at the 52nd percentile of the distribution. [5]
The normality of a distribution can be tested using the test statistic 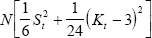 , which
has a chi-squared distribution with two degrees of freedom under the null hypothesis,
where N is the sample size. In December 1982 the null hypothesis of normality
can not be rejected at the 17 per cent level of significance. In all other quarters, the
null hypothesis can be rejected at a significance level of, at most, 0.2 per cent.
[6]
, which
has a chi-squared distribution with two degrees of freedom under the null hypothesis,
where N is the sample size. In December 1982 the null hypothesis of normality
can not be rejected at the 17 per cent level of significance. In all other quarters, the
null hypothesis can be rejected at a significance level of, at most, 0.2 per cent.
[6]
Recall that an exchange rate fall leads to a rise in the price of imports. The coefficient of skewness of quarterly percentage changes of the import-weighted exchange rate index from December 1980 to March 1998 is −0.9. For the trade-weighted exchange rate index the coefficient is −0.7. [7]
The classification of components whose prices are set or largely determined by Government policy is that of Department of Treasury (1995). The components excluded are: Government Owned Dwelling Rents; Local Government Rates and Charges; Household Fuel and Light; Postal and Telephone Services; Automotive Fuel; Urban Transport Fares; Tobacco and Alcohol; Health Services; Pharmaceuticals; and, Education and Childcare. [8]
All seasonal adjustment was conducted using EZ-X11. [9]
Laflèche (1997) notes that some components in the Canadian CPI are priced at set intervals but not each period and so by definition their price changes will be ‘seasonal’. However, with the exception of seasonal clothing, which is a small portion of the total basket, all components of the Australian CPI are priced each quarter. Indeed, work conducted by the Australian Bureau of Statistics suggests that the seasonal pattern in the CPI is weak (Zarb 1991). [10]



