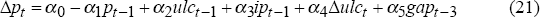RDP 9809: Estimating Output Gaps 3. An Assessment of Estimates of the Output Gap
August 1998
- Download the Paper 387KB
Figure 8 shows estimates of the output gap for each of the five methods examined in Section 2. There are two striking features of these gap estimates. The first is that, at each point in time, there is a range of gap estimates and these sometimes give contradictory indications about whether there is excess capacity in the economy. For example, the linear trend model, some specifications of the univariate and multivariate HP filter models and the unobservable components model indicate that output was above potential at the end of 1997, while other specifications of the HP model and the production function approach indicate the opposite. Indeed, the multivariate HP filter conditioned on the particular NAIRU equation used indicates a large negative gap. The second feature is that all the output gap profiles are similar. Indeed, the correlation coefficients between the various gap measures range between 0.86 and 0.98. This section explores some implications of these two features.
A common characterisation of forward-looking monetary policy is that policymakers set the short-term nominal interest so that its real interest rate component is above its ‘neutral’ value when inflation is expected to be above target and output is expected to be above potential over the forecast horizon.[6] The methods canvassed in the previous section give different and conflicting answers about the output gap at particular points in time, suggesting that it is difficult to uncover the absolute size of the output gap at a point in time. But the result that the profiles of the gap are broadly similar indicates that it is sensible to assess the relative size of the output gap at a particular point in time by comparing the current estimate of the gap to its recent history and to past peaks and troughs.
Some methods are also better than others in gauging the current size of the output gap. An assumption embodied in the univariate techniques is that the output gap is close to zero on average, but this is not the case with multivariate procedures and the production function approach. If the inflation rate has been reduced over the period under consideration, then the average output gap should not be zero. In Australia's case, for example, underlying inflation was reduced from an average 8 per cent from 1980 to 1990, to an average 2½ per cent since then, suggesting that univariate techniques will tend to understate the size of the output gap. Multivariate techniques do not force the output gap to average zero as long as the conditioning processes allow for a persistent wedge in those relationships due to a negative output gap (for example, the gap causing a wedge between the unemployment rate and the NAIRU or between actual and expected inflation). Similarly, the production function does not force the gap to average zero and so may provide a more accurate estimate of the size of the gap at particular points in time (although, as emphasised in Section 2.5, there is still uncertainty associated with this estimate).
The short-comings of the various gap models indicate that judgment is needed in assessing model predictions: models cannot be used mechanistically but form one part of a broad set of information. Mistakes can, of course, be made, but the effects of misjudgments about the output gap are reduced when policy has clear targets. For example, as explained in de Brouwer and O'Regan (1997) in the context of inflation targeting, if policy-makers err in their judgment about the output gap, and set policy too tight or loose, then inflation forecasts will contain systematic errors and inflation will deviate from the target rate and invoke a policy response.
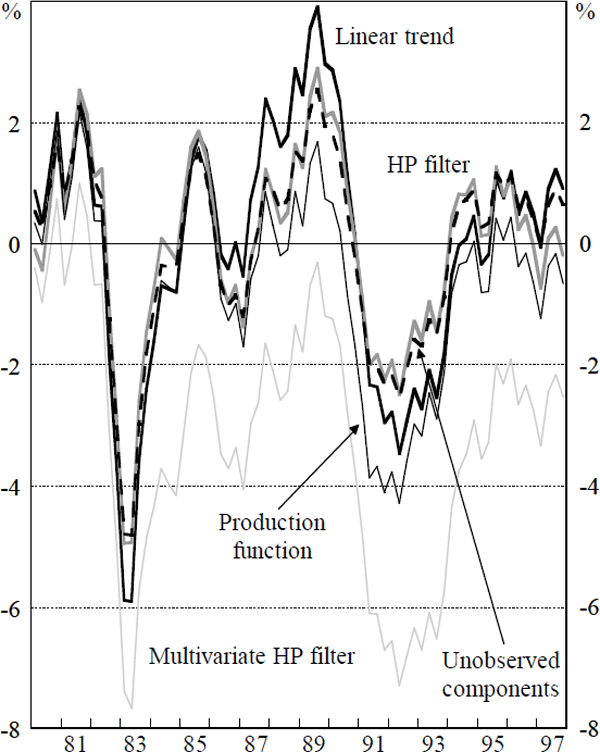
Moreover, the result that the profile of the output gap is broadly consistent across estimation methods indicates that the difference between the measures is essentially a scale effect, which has an important implication for model building. Economic theory and modelling suggest that the output gap can help predict consumer price and wage inflation, implying that the various gap measures can be ranked by how well they help explain price and wage inflation. A simple mark-up model of inflation, written in error-correction format and based on de Brouwer and Ericsson (1995), is used as a benchmark model to assess the performance of the different output gap estimates. The equation is:
where p is underlying consumer prices, ulc is unit labour costs, ip is import prices (adjusted for tariffs), gap is the output gap and α1 = α2 + α3. The third lag of the gap is used since this fits the equation best in all cases. The results are presented in Table 3.
| No gap |
4-quarter-ended growth in output |
Linear gap |
HP gap λ = 1,600 |
MV HP gap |
Unobserved components gap |
Production function gap |
|
|---|---|---|---|---|---|---|---|
| α0 | 0.0065** (0.0006) |
−0.0078 (0.0047) |
−0.007** (0.0005) |
0.0069** (0.0005) |
0.0101* (0.001) |
0.0071* (0.0005) |
0.0083** (0.0006) |
| −α1 | −0.08** (0.01) |
−0.15** (0.02) |
−0.09** (0.01) |
−0.09** (0.01) |
−0.08** (0.01) |
−0.09** (0.01) |
−0.09** (0.01) |
| α2 | 0.05** (0.01) |
0.10** (0.02) |
0.05** (0.01) |
0.05** (0.01) |
0.04** (0.01) |
0.05** (0.01) |
0.05** (0.01) |
| α3 | 0.03** (0.00) |
0.05** (0.01) |
0.04** (0.00) |
0.04** (0.00) |
0.04** (0.00) |
0.04** (0.00) |
0.04** (0.00) |
| α4 | 0.19** (0.03) |
0.21** (0.03) |
0.12** (0.03) |
0.12** (0.02) |
0.10** (0.03) |
0.11** (0.03) |
0.11** (0.03) |
| α5 | – |
0.024** (0.008) |
0.083** (0.014) |
0.112** (0.019) |
0.092** (0.016) |
0.118** (0.019) |
0.104** (0.017) |
| R-bar-sq | 0.870 | 0.884 | 0.906 | 0.909 | 0.908 | 0.911 | 0.912 |
| Q(18) | 0.08 | 0.11 | 0.56 | 0.55 | 0.39 | 0.47 | 0.28 |
| α1 = α2 + α3 | 0.27 | 0.23 | 0.49 | 0.43 | 0.53 | 0.81 | 0.94 |
|
Notes: * and ** indicate significant at the 5% and 1% level. The Q(18) statistic is the marginal significance of the Box-Pierce test that all 18 autocorrelation coefficients of the error are zero. The linear homogeneity restriction is imposed and the marginal significance that the restriction holds is reported in the final row. |
|||||||
The explanatory power of the equation is good even without an output gap since inflation is a very persistent process. But including any of the gap measures improves the fit of the equation, generally by about four per cent in this case, and eliminates serial correlation in the residuals.[7] Moreover, all the output gap measures explain inflation better than just including the current four-quarter-ended output growth.[8] The gap measure that explains output the best is that derived using the production function method outlined in Section 2.5, but this is marginal.
Regardless of the particular measure of the output gap, the movement in the gap over time substantially helps to predict inflation, with the scale effect reflected in the constant and the slope coefficient on the output gap. This is important. In the first place, in empirical models of inflation like Equation (21), the inflationary impulse from the output gap depends on where the output gap is relative to its average value, rather than where it is relative to zero. The various estimates of the gap reported in Table 3 have different averages, and this is reflected in the different constant terms in the estimated equations. Second, in empirical models of inflation like Equation (21), the effect of different cyclical amplitudes in estimates of the output gap on the inflation forecast are ‘washed out’ by different slope coefficients. Estimates of the output gap which produce greater amplitude in the cycle, for example, will tend to have smaller regression coefficients on the output gap in an inflation equation. The ‘fit’ of the equation is similar, even if the estimated parameters vary.
Given that the state of demand is an important source of innovations to price and wage inflation, the inflation prediction error is expected to be considerably higher when the gap is excluded. Table 4 shows how the various gap measures can improve out-of-sample prediction of inflation, reporting the RMSE and absolute mean prediction error for March 1996 to December 1997 when the inflation equations are estimated to the December quarter of 1995. The predictions are based on the actual values of all the independent variables, including the output gap measures.[9] On this basis, the multivariate HP filter and production function measures perform best in predicting inflation, almost halving the inflation prediction error, at least after the fact.
| No gap | 4-quarter-ended growth in output |
Linear gap | HP gap | MV HP gap |
Unobserved components gap |
Production function gap |
|
|---|---|---|---|---|---|---|---|
| RMSE | 0.0030 | 0.0022 | 0.0021 | 0.0026 | 0.0015 | 0.0021 | 0.0016 |
| Mean absolute error | 0.0028 | 0.0020 | 0.0019 | 0.0023 | 0.0014 | 0.0019 | 0.0015 |
|
Note: RMSE is the root mean square error. |
|||||||
Footnotes
See Lowe (ed. 1997) and de Brouwer and Ellis (1998) for a discussion of the literature and related issues. [6]
The output gap also influences unit labour cost growth, so the improvement in fit is even greater when current growth in unit labour costs is excluded from the equation. When this is done, the relative ranking of gap measures does not change. [7]
This holds for both total GDP(A) and non-farm GDP(A). [8]
Each of the gap estimates is based on information over the full sample period and so this test overstates the out-of-sample predictive capacity of the output gap. We do not pursue this here. [9]