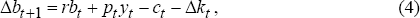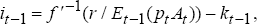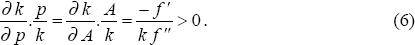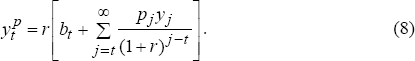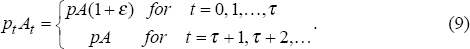RDP 9705: The Response of the Current Account to Terms of Trade Shocks: A Panel-data Study 2. Theoretical Framework

This section describes a simple model of the current account that incorporates the consumption-smoothing and investment effects and highlights the role of the degree of persistence of shocks. The model is of a small open economy facing a given world interest rate. The economy consists of a single infinitely lived representative agent. The agent is assumed to supply one unit of labour inelastically. The agent's problem is to choose the path of investment and consumption so as to maximise lifetime utility, which is given by

where c_t is consumption at time t, δ is the agent's rate of time preference and u(○) is a time-separable utility function with the usual properties, that is, u′ > 0 and u″ < 0. Uncertainty is unnecessary for the basic results and so it is not incorporated into the model.^[3]

There are only two goods in this model, an import good and an export good. The agent consumes only the import good, and the export good is the only good produced domestically. The price of imports is normalised to one, and the price of exports is p_t. Hence, the terms of trade are also equal to p_t. Exports, y_t, are produced according to the following production function,

where k is the level of the capital stock; also, f′> 0 and f″<0. The unit price of capital is fixed and equal to one (by the appropriate choice of units).

The law of motion of the capital stock is

The depreciation rate on capital is set to zero for simplicity.

The agent can borrow or lend on the world capital market at the fixed interest rate r_t = r (denominated in units of imports). The agent's dynamic budget constraint is therefore,

where b_t is the stock of net foreign assets at the beginning of time period t and Δ is the first difference operator. Equation (4) is also the definition of the current account balance which is the change in net foreign assets, Δb_t.^[4]

The optimal level of the capital stock is given by equating the marginal value product of capital to the world interest rate,

Equation (5) shows the optimal level of the capital stock at time t. Implicitly, Equation (5) shows that investment at time t-1 depends on the expectation at t-1 of the terms of trade and productivity at t. That is,

where f′⁻¹(○) is the inverse function of f′(○) and E_t−1(○) is the expectations operator taken at time t−1.

In this very simple model, shocks to the terms of trade have exactly the same effect as productivity shocks. Specifically, the elasticity of the capital stock with respect to the terms of trade is equal to the elasticity of the capital stock with respect to productivity,

A more realistic model would have more than one sector producing goods. In the case of a positive terms of trade shock, the export sectors would expand and the import-competing sectors would contract (non-traded sectors could go either way). In such a model, an increase in the terms of trade would have less of an impact than an equal percentage increase in productivity (across all sectors). However, so long as a positive terms of trade shock leads to an aggregate increase in investment, the results that follow will still hold qualitatively.

In this model, the response of investment is dependent on the duration of the shocks. There is insufficient time to observe and then respond to a purely transitory unanticipated shock. However, for more persistent shocks, investment will respond according to Equation (5). The investment effect by itself leads to a negative correlation between the shock and the current account in the period that the shock is observed.

In reality, the response of investment may be delayed and more drawn out than is implied by this simple model.^[5] This could be due to a number of factors that may exist in the real world, including: delayed learning about the true nature of a shock^[6]; quadratic costs of adjusting the capital stock; and time to install and remove capital equipment (Glick and Rogoff 1995; Obstfeld and Rogoff 1995).

The other choice variable in the agent's maximisation problem, besides investment, is the level of consumption in each period. Consumption behaviour is determined by the Euler equation of this problem:

I assume that δ = r for expositional purposes. Given the assumption of strict concavity of the within-period utility function, this implies a flat consumption path.^[7] Consumption will be equal to the level of permanent income, namely

The consumption-smoothing effect is simply that consumption equals permanent income and, therefore, any differences between permanent and current income are reflected in the current account balance.^[8]

The effect of a shock is best illustrated by a simple example. If p_t = p and A_t = A are constant, then permanent income will equal actual income and the current account will be equal to zero. Starting from this initial steady state at time t = 0, consider a shock to either productivity and/or the terms of trade as follows:

Consider a positive shock, ε > 0 (although the argument is symmetric for negative shocks).^[9] There are three cases to consider depending on the persistence of the shock.

Case 1: The shock is permanent, τ = ∞.

Investment increases today, but the capital stock does not reach its new level until the following period. Hence, current income rises today but by less than permanent income. The consumption-smoothing effect leads to a current account deficit today. The investment effect also causes a current account deficit in the same period that the shock is realised. (A small current account surplus in all future periods ensures that the intertemporal budget constraint is satisfied.)

Case 2: The shock is purely temporary, τ = 0.

There is no investment effect because there is not enough time to react to the shock. Current income rises by more than permanent income and so the consumption-smoothing effect implies a current account surplus at the time of the shock.

Case 3: The shock is temporary but persistent, 0 < τ < ∞.

Now permanent income rises by less than current income.^[10] The consumption-smoothing effect leads to a current account surplus in all periods from t = 0 to τ. The magnitude of the consumption-smoothing effect is decreasing with higher persistence, τ, because permanent income is closer to current income, the greater the persistence of the shock. The investment effect leads to a current account deficit in the period that the shock occurs. The net effect of consumption-smoothing and investment depends on the degree of persistence of the shock. For less persistent shocks, the consumption-smoothing effect will dominate and there will be a positive correlation between the shock and the current account (in the period of the shock). For some degree of persistence, the two effects will cancel each other out. At higher degrees of persistence, the investment effect will dominate and there will be a contemporaneous negative correlation between the shock and the current account.

The key to this paper was to identify two groups of countries based on the degree of persistence of their terms of trade shocks – those with more temporary shocks for which the consumption-smoothing effect should dominate and those with very persistent shocks for which the investment effect should dominate. This is taken up in Section 4 of the paper after a preliminary look at the data in Section 3.

Footnotes

Uncertainty is discussed later in the paper when it becomes relevant to the estimation methodology. [3]

Also, there is the transversality condition, 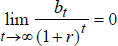, which prevents the agent from building up debt to levels so high that it can only be financed by rolling over the debt by further borrowing. [4]

Also, consumption may not adjust instantaneously to shocks. I ignore this issue by presuming that consumption responds more rapidly than investment. [5]

This is particularly important if investment involves fixed costs. [6]

With δ ≠ r the consumption path has a trend. The current account will also exhibit a trend except for the special case where the paths of A_t and p_t imply the same trend for both consumption and income. These possibilities are dealt with in the empirical section of this paper by detrending all of the series. [7]

Actual income is equal to the sum of interest income on net foreign assets and export income, rb_t + p_ty_t. [8]

It is possible that a persistent large negative terms of trade shock could lead to significant investment in an industry which had so far been relatively minor – for example, the first oil shock could have led to significant investment (and hence, current account deficits) to exploit previously untouched oil resources. However, this did not appear to be relevant for any of the countries with very persistent terms of trade shocks (Section 4.3). [9]

Although this need not be the case for a very persistent shock. In this case, at time t = 0, it could be that the one period delay in the capital stock adjustment means that current income is less than permanent income, in which case the story is much like in the case where τ = ∞. [10]