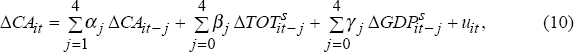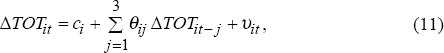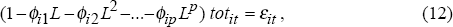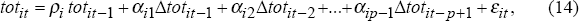RDP 9705: The Response of the Current Account to Terms of Trade Shocks: A Panel-data Study 4. Panel-data Regressions
October 1997
- Download the Paper 163KB
4.1 Methodology
To begin with, I used a panel-data regression to estimate the dynamic relationship between the current account and the terms of trade across the full set of countries. Then, two groups of countries were identified – one group that tended to have highly transitory terms of trade shocks, and the other group that tended to have highly persistent terms of trade shocks. Finally, the regression analysis was repeated using these two country groupings to test the persistence hypothesis.
Panel data was more appropriate than individual-country regressions given the limited number of annual observations and large number of countries in the sample. Also, panel regressions allowed countries to be grouped together according to the degrees of terms of trade persistence. The panel-data regression was of the following basic form:
where: ΔCAit is a transformation of the annual current account balance (as a per cent of nominal GDP, for country i at time t) obtained by demeaning the first difference of the original series; ΔTOTs is the shock or innovation (see below) to the annual growth rate of the terms of trade; and ΔGDPs is the shock to the annual growth rate of real GDP. Exact details of the original series and their sources are provided in Appendix B.[14]
There are some important issues related to the choice of this specification that need to be addressed, including the inclusion of real GDP, the nature of the transformations of the variables, the identification of shocks, the lag structure and the question of exogeneity.[15]
The theory discussed in Section 2 implies that changes in productivity are likely to be an important determinant of the current account. However, for many countries in this study, data on productivity are unavailable or at best very unreliable. Real GDP growth was used as a proxy for productivity growth. I checked that this would not affect the results significantly by using the set of OECD countries[16] for which somewhat reliable estimates of the Solow residuals exist. Specifically, I ran the regressions first with the Solow residuals and then with real GDP growth in place of the Solow residuals. The results were very similar and suggested that this substitution would not bias the results for the full set of countries. I do not report the results for the OECD-country regressions (they are available upon request).
As well as reflecting productivity shocks, real GDP growth also captures cycles in demand. However, I expect that the current account response should be similar for both demand and supply shocks. That is, following a positive demand shock, the current account should fall because the increase in investment will be likely to dominate a rise in savings. It is a stylised fact of business cycles that both investment and consumption are procyclical, and that investment is more variable than output which in turn is more variable than consumption. Hence, both investment and savings will typically rise with output. However, the rise in investment should dominate because the ratio of investment variability to output variability is typically much higher than the ratio of output variability to consumption variability.[17]
The data were transformed so as to ensure that all variables were integrated of order zero, which was necessary for valid statistical inference. Tests of stationarity (discussed in detail later in this section) revealed that a large number of countries showed evidence of non-stationary terms of trade in levels, while others showed evidence of stationarity. The level of real GDP is likely to be non-stationary (even about a deterministic trend) for most countries.[18] Finally, the current account balance shows evidence of trend behaviour within the sample period for some countries.[19] Differencing the current account along with the other variables avoids the problem of spurious regressions due to either stochastic or deterministic trends.
4.1.1 Identifying shocks
The objective of this section is to measure the response of the current account to unexpected changes in the terms of trade. Terms of trade changes may contain a predictable component. In this case the terms of trade changes will be an imperfect proxy for terms of trade shocks.[20],[21] Shocks to the terms of trade were constructed for each country as the estimated residual from the following regression:
where, ΔTOTit is the growth rate of the terms of trade in country
i at time t, and ci is a constant term
for country i. The terms of trade shock is 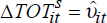 . This specification
used three lags of the growth rate of the terms of trade to be consistent with
the results of the Augmented Dickey-Fuller tests conducted later on in this
section. Shocks to the growth rate of real GDP were constructed in a similar
fashion for
consistency.[22]
. This specification
used three lags of the growth rate of the terms of trade to be consistent with
the results of the Augmented Dickey-Fuller tests conducted later on in this
section. Shocks to the growth rate of real GDP were constructed in a similar
fashion for
consistency.[22]
Equation (10) is a fixed effects model because the data have already been demeaned country by country. Hence, there was no need for a constant term in Equation (10).[23]
The lag structure of Equation (10) was chosen for a number of reasons that are not apparent from the simple theory of Section 2. In particular, this structure allowed for uncertainty and adjustment costs. If investment involves quadratic adjustment costs, as in Glick and Rogoff (1995), the adjustment of the capital stock will be gradual. If investment involves fixed costs, then the adjustment could be delayed. Delayed adjustment of both consumption and investment will in part depend on uncertainty – it may take time to observe shocks and determine their likely size and persistence.[24]
Another source of dynamics comes from contracts which lock in the real level of imports and exports for some time. This possibility, as well as the time it takes to observe and then react to a shock, suggests an automatic positive correlation between the current account and the contemporaneous terms of trade. To the extent that this lack of response is not optimal, the current account will adjust in periods following the terms of trade shock.
When estimating Equation (10), it was assumed that the terms of trade and productivity growth (proxied by real GDP growth) were both exogenous with respect to the current account. For the terms of trade, this assumption was certainly valid for most of the ‘small’ countries in the sample, that is, those countries that have little influence on world prices. The possible endogeneity for a few large countries was ignored, other than to be careful that country groupings were not dominated by large countries. However, the influence of the Organisation of Petroleum Exporting Countries on oil prices was considered important and is accounted for below.
The causality running from the current account to the productivity shocks is tenuous and likely to be indirect.[25] For developing countries in particular, the level of imports of new capital equipment will embody new technology and therefore affect the productivity level. However, capital equipment is only a part of total imports of goods and services which in turn is only a component of the current account.
Before discussing the crucial topic of the terms of trade persistence, I present the results for the full set of countries. This provides a useful base line comparison for later country group results.
4.2 Results for the Full Set of Countries
The panel-data regressions for the full set of countries were based on a set of 96 countries. Data limitations meant that many of the 128 countries used in Section 3 were excluded from the regression analysis. Countries that had all the necessary series over the years 1970 to 1992 (as marked in Table A1) were included in the regression analysis. A few countries had missing current account data for one year of the sample, usually 1970 (Appendix A). To enable these countries to remain in the sample, these missing country years were dealt with by running an unbalanced panel-data regression.[26]
The estimation procedure was Feasible Generalised Least Squares, which was used to correct for heteroskedasticity across countries.[27] The estimates of both the full and the parsimonious model are reported in Table 3 below. The preferred model here and in the rest of the paper is the parsimonious model that is obtained by eliminating lags of variables with insignificant coefficients.
| Full model | Parsimonious model | ||||
|---|---|---|---|---|---|
| Variable | Lag | Coefficient (t-statistic) | |||
| ΔCA | 1 | −0.265 | (−10.14) | −0.259 | (−9.94) |
| 2 | −0.258 | (−11.18) | −0.270 | (−12.34) | |
| 3 | −0.137 | (−5.99) | −0.153 | (−6.96) | |
| 4 | −0.126 | (−5.60) | −0.131 | (−5.90) | |
| ΔTOTs | 0 | 0.077 | (11.79) | 0.078 | (11.93) |
| 1 | −0.024 | (−4.23) | −0.024 | (−4.10) | |
| 2 | −0.010 | (−1.86) | – | ||
| 3 | −0.006 | (−1.22) | – | ||
| 4 | −0.019 | (−2.93) | −0.018 | (−3.65) | |
| ΔGDPs | 0 | −0.135 | (−6.86) | −0.137 | (−6.97) |
| 1 | −0.074 | (−4.82) | −0.076 | (−4.96) | |
| 2 | −0.033 | (−2.18) | −0.040 | (−2.51) | |
| 3 | 0.020 | (1.32) | – | ||
| 4 | −0.031 | (−2.20) | −0.036 | (−2.52) | |
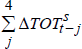 |
0.016 |
(1.31) |
0.036 |
(3.71) |
|
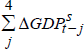 |
−0.253 |
(−6.31) |
−0.288 |
(−8.22) |
|
| No. Obs 1,824 | No. Obs 1,824 | ||||
| R2 = 0.28 | R2 = 0.27 | ||||
| Notes: Standard errors obtained by using the ROBUSTERRORS command in RATS (damp set to one and lags set to 4). This provides Newey-West estimates of the covariance matrix corrected for heteroskedasticity and for serial correlation of a moving average of order 4. | |||||
The results from the parsimonious model show that across the 96 countries, on average, a large positive shock to the terms of trade has a small but significant positive effect on the current account over a five-year period following the shock. The year by year effects indicate that the current account rises in the same year as a positive shock to the terms of trade shock and then falls in following years. Productivity shocks (via the proxy of real GDP growth) have the expected negative effect on the current account in all years following the shock.
4.3 Stationarity, Persistence and Trends in the Terms of Trade
The stationarity and persistence of the terms of trade are closely related and are crucial to both the methodology and the interpretation of the results. The ADF test was used to determine whether each terms of trade series is stationary or non-stationary, as well as to provide an estimate of the persistence of terms of trade shocks. The underlying model was assumed to be an autoregressive process for the logarithm[28] of the terms of trade with lag length, p, as follows:
where L is the lag operator and totit is the logarithm of the terms of trade for country i at time t. A natural measure of persistence for country i is
From the Beveridge-Nelson decomposition, it follows that this model can be rewritten in the form of the ADF test,
where 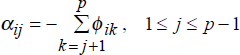 .
.
The null hypothesis is that the terms of trade is integrated of order one, I(1),
in other words, that ρi = 1. The standard form of the test also allows for
a constant and a time trend in Equation (14). The lag length, p, was
chosen to give a parsimonious model while ensuring that the estimated residuals,
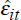 ,
showed no sign of serial correlation. The tests were conducted on each country's
terms of trade over the full length of data available for that country.
,
showed no sign of serial correlation. The tests were conducted on each country's
terms of trade over the full length of data available for that country.
The objective was to choose two groups of countries according to the persistence of their terms of trade. One obvious criteria was stationary versus non-stationary terms of trade. However, the results of the ADF tests were not clear for all countries. In particular, results often depended on borderline decisions regarding the appropriateness of a deterministic trend, or whether to use 5 or 10 per cent critical values. In part, the problem was that these tests suffer from weak power which is particularly true for small sample sizes.
Ideally, countries would have been split into different groups according to ex ante information regarding the behaviour of their terms of trade, not ex post information such as I have used. However, this was not possible because of the already limited sample size. Instead, I adopted an approach that identified those countries with terms of trade that were at the extreme ends of the spectrum of terms of trade persistence. In this way, each grouping contains countries that can be considered most likely to have had either the most or the least persistent terms of trade shocks ex ante.[29]
4.3.1 Least persistent terms of trade country group
The critical criteria for inclusion in this grouping was a stationary terms of trade. I chose a group of 10 countries based on stationarity around a mean (using a 10 per cent significance level). Countries with trend-stationary terms of trade were excluded because I felt that it would be hard for agents to differentiate between a trend and a preponderance of persistent shocks in one direction.[30]
The 10 countries included in the least persistent group were: Finland, Iceland, Israel, Jamaica, Jordan, the Republic of Korea, Mali, New Zealand, Panama and the United Kingdom. The average estimate of persistence for this group was 0.58.
4.3.2 Most persistent terms of trade country group
The criterion for inclusion in the most persistent group was a non-stationary terms of trade with a point estimate of persistence above 0.85 under two different tests. The first was an ADF test including both a trend and a constant; the second was an ADF test with a constant but no trend. Both tests were done with lags, p, set equal to 3 and at the 5 per cent level of significance.[31] The point estimates of persistence from both of these tests are provided for all 128 countries in Table A1. Some countries have terms of trade that display a high degree of persistence as measured by the ADF test, including both a trend and a constant but not with a constant alone (and vice versa). Hence, it was thought that countries meeting both of these tests would be most likely to have had ex ante very persistent terms of trade.
The influence of the two oil price shocks is strongly evident in the terms of trade of many countries meeting these criteria. A further refinement was to exclude members of OPEC from this set because these countries influenced their terms of trade by restricting sales and production of oil and, presumably, investment in their oil industries.[32] Therefore, to the extent that the cartel was successful, OPEC members should have the consumption-smoothing effect dominating the investment effect, whereas theory suggests the opposite for countries with highly persistent terms of trade shocks.
The set of 11 countries satisfying the conditions for very persistent terms of trade were: Bolivia, Botswana, Canada, Italy, Kenya, South Africa, Spain, the Syrian Arab Republic, Tanzania, Trinidad and Tobago and the United States. It turns out that for this group the null hypothesis of a random walk in the terms of trade cannot be rejected.
4.4 Results Based on Persistence of Terms of Trade Shocks
The theory outlined in Section 2 implies that more persistent terms of trade shocks will be negatively correlated with the current account while more temporary shocks will be positively correlated. Before presenting the evidence from the panel-data regressions, it is worth reviewing the results from counting correlation episodes in Section 3 in the light of the two groups of countries above. Recall that a correlation episode describes the response of the current account to large movements in the terms of trade over periods of one and two years. Countries within the higher persistence group should have had relatively more episodes of negative correlations between the current account and large terms of trade changes than those of the low persistence group. The average number of positive, negative and zero correlation episodes per country within each group is shown in Table 4.
| Average number of correlation episodes per country | |||
|---|---|---|---|
| Positive | Zero | Negative | |
| 11 countries with highest terms of trade persistence | 3.9 | 7.4 | 3.6 |
| 10 countries with lowest terms of trade persistence | 5.0 | 8.9 | 2.3 |
These results are broadly consistent with the theory that persistence is an important determinant of the dynamics of the current account with respect to terms of trade shocks. Countries with the most persistent terms of trade shocks have had on average more negative correlations (3.6 compared to 2.3) and less positive correlations (3.9 compared to 5.0) than countries with the least persistent terms of trade shocks.
This finding was confirmed by the results of panel-data regressions on the high and low persistent country groupings in Table 5.
| 11 countries with highest TOT persistence | 11 countries with lowest TOT persistence | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Full model(a) | Parsimonious model | Full model(a) | Parsimonious model(a) | ||||||
| Variable | Lag | Coefficient (t-statistics) | |||||||
| ΔCA | 1 | −0.198 | (−2.40) | −0.161 | (−2.50) | −0.322 | (−3.80) | −0.307 | (−4.05) |
| 2 | −0.114 | (−1.77) | – | −0.424 | (−6.05) | −0.409 | (−6.13) | ||
| 3 | −0.202 | (−3.52) | −0.184 | (−2.90) | −0.186 | (−2.95) | −0.180 | (−3.35) | |
| 4 | −0.110 | (−1.84) | – | −0.177 | (−2.70) | −0.165 | (−2.95) | ||
| ΔTOTs | 0 | 0.072 | (2.63) | 0.070 | (3.85) | 0.128 | (2.67) | 0.124 | (2.78) |
| 1 | −0.055 | (−2.05) | −0.056 | (−3.03) | 0.024 | (0.58) | – | ||
| 2 | −0.033 | (−1.58) | −0.041 | (−2.19) | 0.005 | (0.16) | – | ||
| 3 | −0.005 | (−0.31) | – | −0.025 | (−0.91) | – | |||
| 4 | −0.051 | (−2.55) | −0.049 | (−2.64) | 0.019 | (0.73) | – | ||
| ΔGDPs | 0 | −0.197 | (−3.84) | −0.202 | (−4.62) | −0.158 | (−2.15) | −0.146 | (−1.98) |
| 1 | −0.002 | (−0.04) | – | −0.190 | (−2.72) | −0.185 | (−2.60) | ||
| 2 | −0.046 | (−1.00) | – | −0.107 | (−1.91) | −0.123 | (−2.01) | ||
| 3 | 0.020 | (0.51) | – | −0.162 | (−2.07) | −0.159 | (−2.13) | ||
| 4 | 0.012 | (0.30) | – | −0.043 | (−0.62) | – | – | ||
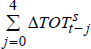 |
−0.072 |
(−1.77) |
−0.077 |
(−2.13) |
0.150 |
(1.86) |
0.124 |
(2.78) |
|
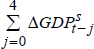 |
−0.213 |
(−1.87) |
−0.202 |
(−4.62) |
−0.662 |
(−3.46) |
−0.612 |
(−4.07) |
|
| No. Obs 209 | No. Obs 209 | No. Obs 190 | No. Obs 190 | ||||||
| R2 = 0.34 | R2 = 0.31 | R2 = 0.30 | R2 = 0.30 | ||||||
| Notes: (a) Indicates standard errors corrected for heteroskedasticity and for serial correlation. | |||||||||
For countries with highly persistent terms of trade, the sum of coefficients on the terms of trade shocks was significantly negative (at the 5 per cent level). For countries that have the least persistent terms of trade, the coefficient on the contemporaneous terms of trade shock was positive and was the only significant lag in the regression. The coefficient on real growth (as a proxy for productivity shocks) was significantly negative, which was expected given the high degree of persistence of these shocks. As predicted by a model with more than two sectors, the effect of real growth was much larger in absolute value than the effect of the terms of trade.
The impulse response functions in Figure 3 show the cumulative effect of a 1 per cent shock to the terms of trade on the current account for each of the three parsimonious models. The upper impulse response is based on the sample of 10 countries with the least persistent terms of trade, the middle impulse response is based on the full set of 96 countries, and the lower impulse response function is based on the sample of 11 countries with the most persistent terms of trade. In all cases, the current account rises initially, but this is reversed in subsequent years. The current account quickly moves towards a deficit in the case of countries for which the shock is persistent. This is consistent with a lagged investment effect dominating any consumption-smoothing effect. For countries that experience predominantly temporary terms of trade shocks the consumption-smoothing effect appears to dominate and the current account moves towards a surplus.
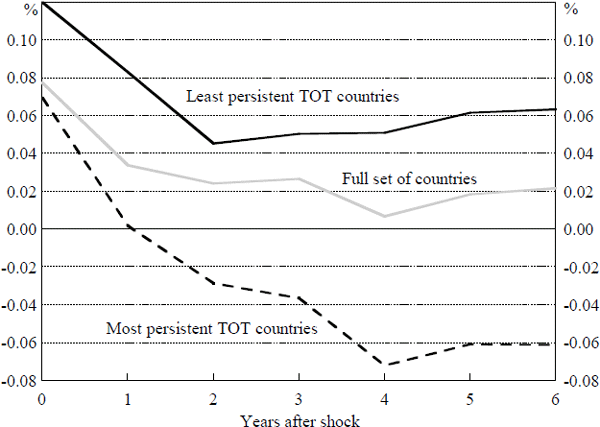
Bootstrap techniques were used to provide 95 per cent confidence intervals around each of the impulse response functions. The confidence intervals (shown in Figure A1 in Appendix A) clearly show that after four years the response of the current account to a terms of trade shock was positive for the 10 countries with the least persistent terms of trade and negative for countries with the most persistent terms of trade. Furthermore, the confidence interval for the full set of 96 countries lies around zero and strictly between estimates for the two extreme persistence groupings after four years.[33]
The standard deviation of the terms of trade shocks across countries was 13.5 and 9 per cent for the most and least persistent terms of trade country groups respectively. The current account response to positive shocks of this size after four years was a fall in the current account balance of almost one percentage point for the most persistent terms of trade countries and a rise in the current account of about half a percentage point for the least persistent group.
Footnotes
Because the changes in the terms of trade are often very large, the log difference is not a good approximation of the growth rate of this series. Therefore, growth rates of the terms of trade and real GDP were both calculated as year-to-year percentage changes. [14]
One extension considered, but not presented here, was to weight each country's terms of trade by a measure of openness (exports plus imports as a per cent of GDP). This would control for the fact that the current account of a very closed country should respond less to a terms of trade shock than a very open country. However, this weighting scheme did not substantially alter the conclusions and only made the interpretation of the elasticities difficult. Also, the two country groupings developed below have similar distributions of openness. [15]
Luxembourg was excluded from the results. This left 23 OECD countries in the sample. [16]
For a summary of stylised real business cycle facts for a number of countries, see Danthine and Donaldson (1993). [17]
Glick and Rogoff (1995) have shown that the Solow residuals of the G-7 countries follow a random walk in levels (based on manufacturing data). Therefore, shocks to productivity are permanent or, at the very least, very persistent. [18]
As mentioned before, this trend behaviour could be due to differences between a country's discount rate and the world interest rate and/or expectations of trends in productivity or the terms of trade. [19]
Except in the case where the terms of trade follows a random walk, which appears to be the case for many countries with very persistent terms of trade shocks. [20]
The use of the actual changes in the terms of trade and real GDP (as imperfect proxies for the shocks) in the estimation of Equation (10) biases coefficient estimates towards zero but it did not substantially alter the main findings (these results are not reported). [21]
The sample size was not sufficient to allow the construction of ex ante shocks by using recursive regressions (that is, the first regression in the recursion would require a sample that ends just prior to the start of the sample period used in the panel-data regressions). [22]
However, all standard errors reported in the paper have the appropriate degrees of freedom correction that accounts for the fact that country means are estimated before panel-data regressions were conducted. [23]
For example, in the early stages of the Gulf War of 1990/91, the oil price rose dramatically then fell back towards pre-war levels before the end of the year. [24]
A very indirect link would be through the potential for a large shock to the current account to induce changes in the real exchange rate that lead to changes in sectoral composition and, hence, aggregate productivity changes. [Thanks to Richard Eckaus for pointing out this link.] [25]
Starting the sample period for all countries in 1971 would eliminate the 1974 oil shock when four lags of the current account are included on the right-hand side of Equation (10). [26]
Estimates of variance of the residuals used in FGLS were based on the fully specified model, not on the more parsimonious models reported below. However, any residual heteroskedasticity was corrected by using the Newey-West estimates of the final covariance matrix. [27]
The logarithm is not a good approximation for the growth rate as discussed in a previous footnote. However, in this case it is necessary to use the logarithm so as to follow the ADF procedure which requires the variable in levels and first differences. [28]
The terms of trade may consist of both temporary and permanent components; however, the objective was to identify countries for which one of these components dominated the other. [29]
A criteria based on stationarity around a mean, at a 5 per cent significance level,
left too few countries in the sample. Other possibilities that were investigated
included stationarity (including trend stationarity) at a 5 per cent significance
level with a point estimate of persistence, 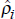 ,
below 0.55. Results for this group of 15 countries were consistent with those
reported below. These 15 countries were: Australia, Bangladesh, Costa Rica,
Finland, Jamaica, Jordan, Malawi, Mali, Morocco, Papua New Guinea, Portugal,
Sudan, Thailand and Uruguay.
[30]
,
below 0.55. Results for this group of 15 countries were consistent with those
reported below. These 15 countries were: Australia, Bangladesh, Costa Rica,
Finland, Jamaica, Jordan, Malawi, Mali, Morocco, Papua New Guinea, Portugal,
Sudan, Thailand and Uruguay.
[30]
Three lags were sufficient for most countries to remove any serial correlation in the residuals of Equation (14). Relaxing the criteria to be either p equals 3, 2 or 1 did not alter the results substantially from those presented below. [31]
That is, the terms of trade is not exogenous for the case of OPEC countries. [32]
In the long run, the path of the current account should satisfy the intertemporal budget constraint and the transversality condition. That is, if the shock causes the current account to increase for a while, eventually the current account should decrease below its original position (and vice versa if the current account decreases following the shock). However, the estimation technique did not include enough lags to account for longer-run behaviour. Adding more lags of the current account to the model provided tentative evidence that in all three cases the current account moves closer towards balance five and six years after the shock. [33]