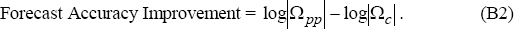RDP 9704: Financial Aggregates as Conditioning Information for Australian Output and Inflation Appendix B: Technical Description of the Conditional Forecasting Exercise

In each exercise, we use a four-variable VAR to calculate an estimated forecast error covariance matrix of one- through eight-quarter-ahead forecasts of the indicated policy variable.^[19] We denote this forecast error covariance matrix as Ω_pp, where p refers to policy variable.^[20] The forecast error covariance matrix summarises the degree of variation in either real output growth or inflation not explained within the model using information up to period t. The diagonal elements of the error covariance matrix are the variance terms of the one- through eight-step-ahead forecast error of the policy variable, whereas the off-diagonal elements are the covariances between the forecast errors across the one- through eight-period forecast horizons. The log determinant of this covariance matrix is used as a measure of unconditional forecast accuracy for either real output growth or inflation, given by log |Ω_pp|.^[21] For example, if the forecasts become more accurate, then the forecast errors become smaller as does the log determinant of the forecast error covariance matrix. The predominant contributors to the measure of forecast accuracy are typically the own error variance terms, that is, the diagonal terms. The log determinant of the error covariance matrix would get successively smaller as more values of the other three variables in the VAR became available as certain information.^[22]

This prediction exercise focuses on the covariance between forecast errors of financial aggregates and of real output growth and inflation. We use the same full-sample estimation of the VAR model to derive an estimate of the covariance matrix of the same forecast, conditioned on certain knowledge of the next eight quarters of the given financial aggregate. In order to examine the contribution of information on financial aggregates, we must create a measure of conditional forecast accuracy. For the succeeding eight quarters of a given financial aggregate a, we define Ω_aa similarly to the unconditional forecast error covariance matrix of the policy variables, but allow it to represent the (unconditional) forecast error covariance of the financial aggregate for the eight-period forecast horizon. Separately, we define Ω_ap and let it represent the forecast error covariance matrix between the financial aggregate and the policy variable of interest (either output growth or inflation). In this covariance matrix, the diagonal terms represent the covariance between the forecast errors of the financial aggregate and those of either real output growth or inflation at the same forecast horizon. For example, the first diagonal term represents the covariance of the financial aggregate with a policy variable at the one-period forecast horizon, and so on until the last diagonal term reflecting the correlation at the eight-period forecast horizon. The off-diagonal terms represent the covariance between forecast errors of the financial aggregate and the policy variable across different forecast horizons.

Unconditional forecast errors for the policy variable in this setting implicitly contain covariation in errors from forecasting the other variables in the system with the errors in forecasting the policy variable. Comparable to a variance decomposition, we can measure the contribution of each variable in the system to the forecast error in the policy variable. Eliminating forecast errors in the financial aggregate series (that is, providing perfect knowledge of future values of the variable) is like removing the covariation of forecast errors in the financial aggregate with those in the policy variable (either real output growth or inflation) and the related contribution to the unconditional forecast error of real output growth or inflation. That is the intuitive motivation behind Equation (B1) below.

By manipulating the estimated forecast error covariance matrixes, we essentially compare how the contribution of certain knowledge of the aggregates reduces the measure of forecast accuracy. Defining Ω_c as the conditional error covariance matrix,

we subtract the component of the forecast error covariance in the variable of interest that is removed when the financial aggregate for the next eight periods is known with certainty. Here, we eliminate the component of forecast error covariance of the policy variable that knowledge of the financial aggregates will remove. That is, knowing the measure of the financial aggregate removes the forecast error variance of these measures over the eight-period forecast horizon from the system, and thus removes the contribution of that forecast error variance to the forecast error variance for the policy variables. Thus, the log determinant of Ω_c, given by log|Ω_c|, becomes our measure of conditional forecast accuracy. The focus of our attention then become the difference between the measures of conditional and unconditional forecast accuracy, denoted as,

Footnotes

The following description relies heavily on pages 148–49 of Roberds and Whiteman (1992). [19]

This matrix measures forecast error covariances calculated within the sample using a model with parameters estimated employing the entire sample data period. Thus, the forecast errors are in-sample forecast errors; this artificial test of in-sample forecast improvement is distinct from the out-of-sample tests in Tallman and Chandra (1996). [20]

Log determinant measures are used in standard likelihood ratio tests in VAR analyses. For our purposes, the log determinant measure is somewhat analogous to a mean squared error measure in a single-equation forecasting statistic, but it is more general because of the covariance terms among the eight-period horizon forecasts. [21]

This formulation of forecast error variance is comparable to the variance decomposition in VAR analysis, whereby the forecast errors in a variable are associated with innovations in each variable in the system. Unlike the variance decomposition, this technique need not orthogonalise innovations. [22]