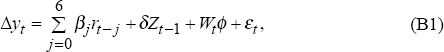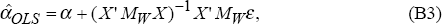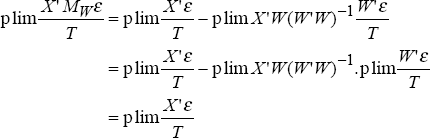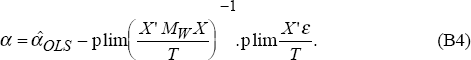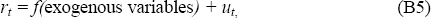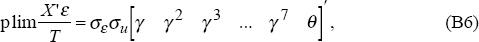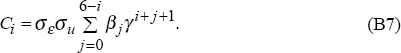RDP 9702: The Implementation of Monetary Policy in Australia Appendix B: Estimating the Bias from Ordinary Least Squares

It is convenient to rewrite the model for non-farm GDP growth, Equation (1) in the text, as

where Z_t−1 = y_t−1 − χ^*w_t−1 (χ^* is the cointegrating vector between y and w) and W_t is the matrix of exogenous variables, W_t = [1 Δw_t Δw_t−1 Δf_t−2 Δf_t−4]. Equation (B1) may be further simplified to

where X_t = [r_t r_t−1 r_t−2 r_t−3 r_t−4 r_t−5 r_t−6 Z_t−1] is the matrix of regressors presumed to be correlated with the disturbance term, ε_t.

OLS on Equation (B2) yields the following estimate for α,

where M_W = I − W(W′W)⁻¹W′.

Now,

as plim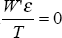 since W is exogenous. In the limit, as the sample size increases, the true value of the vector α is then

We presume that the short-term real interest rate, r_t, can be expressed as

where ‘exogenous’ implies uncorrelated with the error term in Equation (B2) and u_t is determined by the policy-maker on the basis of information about current and future output not available to the econometrician estimating the output equation (B2).

As explained in the text, the correlation coefficient between real interest rates and the error term in Equation (B2) is assumed to be a geometrically declining function of the lag of the real interest rate, with no correlation after the sixth lag. The covariance between Z_t−1 and ε_t (which is identical to the covariance between y_t−1 and ε_t) is denoted σ_ε σ_u θ and is derived below. In symbols we have

where σ_ε and σ_u are estimates of the standard deviations of the errors in Equations (B1) and (B5). For the underlying model, σ_ε = 0.56, while for σ_u, we use the value derived from estimating Equation (3) in the text (which is a simple version of Equation (B5)). This gives the estimate σ_u=1.32.

Now define the variables C_i, i = 0,...,6 by

Denote the covariance between ε_t and y_t−i as PL_i, and between ε_t and Δy_t−i as PC_i. The model, Equation (B2), implies the recursive structure,

We require θ = PL₁/σ_εσ_u, which is a function of the true vector α. For given γ in the range zero to 0.75, we proceed as follows. First, we use the sample value of 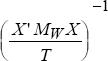as our estimate of plim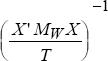. (This requires an estimate of the cointegrating vector, χ^*, between y and w; we use the OLS estimate for this.) Next, we use the OLS estimate, 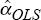to generate an estimate 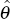via Equation (B8). We now have an estimate for plim 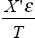via Equation (B6). 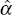This enables us to generate an estimate, , of the ‘true’ vector α via Equation (B4). We now iterate: 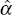implies a new estimate for θ, 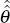, which, in turn, implies a new estimate for α, 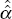. This process is continued until it converges, yielding . 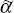The estimated response to a permanent 1 per cent increase in the real interest rate on year-ended growth shown in Figure 4 and on the average lag of monetary policy shown in Figure 5 are generated using 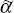.