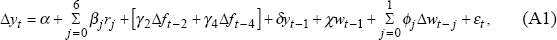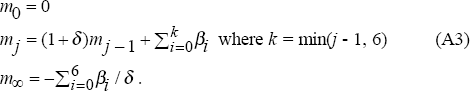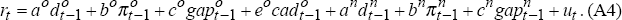RDP 9702: The Implementation of Monetary Policy in Australia Appendix A: Monte Carlo Procedure
April 1997
- Download the Paper 247KB
This appendix outlines the Monte Carlo procedure used to generate confidence intervals for the OLS, IV and recursive regressions.
A.1 Ordinary Least Squares Regressions
The non-farm output equation, rewritten here for convenience, is
which may be simplified to
where Nt is the vector of explanatory variables excluding yt−1.
A sustained one per cent rise in the real interest rate leads to an effect on the level of output after j quarters (mj) of:
Estimating Equation (A2) by OLS over the 63 quarters 1980:Q3 to 1996:Q1 leads to
parameter estimates 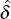 and
and 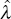 ,
and an estimate of the standard deviation of the errors, σε
= 0.56, for both the underlying and headline models. The Monte Carlo distribution
is then generated by running 1,000 trials with each trial, i, proceeding
as follows:
,
and an estimate of the standard deviation of the errors, σε
= 0.56, for both the underlying and headline models. The Monte Carlo distribution
is then generated by running 1,000 trials with each trial, i, proceeding
as follows:
-
draw a sequence of observations
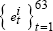 from a normal distribution
with mean 0 and variance
from a normal distribution
with mean 0 and variance 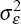 ;
;
-
generate sequences of synthetic data
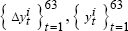 using
using 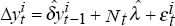 and
and 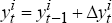 , where
, where 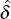 and
and 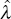 are from the OLS
estimation using the original data;
are from the OLS
estimation using the original data;
-
use the synthetic data to estimate the equation
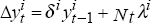 , by OLS and hence
generate parameter estimates
, by OLS and hence
generate parameter estimates 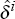 and
and 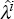 ; and
; and
-
with these parameter estimates, use Equation (A3) to calculate, for this ith
iteration, the effect of a one per cent rise in the real interest rate on
the level of output (
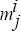 , j = 1,...,12, ∞) and the
year-ended growth rate of output
, j = 1,...,12, ∞) and the
year-ended growth rate of output 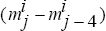 after j
quarters.
after j
quarters.
The figures in the text show the 5th, 50th and 95th percentile values for
the effect on the level of output, 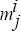 , and on the year-ended
growth rates,
, and on the year-ended
growth rates, 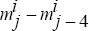 .
.
A.2 Instrumental Variable Regressions
The policy reaction function, rewritten for convenience, is
Estimating the underlying CPI version of Equation (A4) by OLS over the 63 quarters
1980:Q3 to 1996:Q1 leads to fitted values  ,
and an estimate of the standard deviation of the errors, σu
= 1.32. Diagnostic tests on the sample errors reveal strong signs of first-order
autocorrelation, with an estimated autocorrelation coefficient,
,
and an estimate of the standard deviation of the errors, σu
= 1.32. Diagnostic tests on the sample errors reveal strong signs of first-order
autocorrelation, with an estimated autocorrelation coefficient, 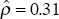 .
.
Estimating Equation (A2) by IV, using 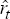 as an instrument for rt over the period 1980:Q3 to 1996:Q1 leads
to parameter estimates
as an instrument for rt over the period 1980:Q3 to 1996:Q1 leads
to parameter estimates 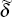 and
and 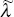 , and an estimate
of the variance-covariance matrix of the errors from Equations (A2) and (A4),
, and an estimate
of the variance-covariance matrix of the errors from Equations (A2) and (A4),
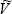 .
The Monte Carlo distribution is then generated by running 1,000 trials with
each trial, i, proceeding as follows:
.
The Monte Carlo distribution is then generated by running 1,000 trials with
each trial, i, proceeding as follows:
-
draw two sequences of observations
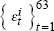 and
and 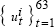 from a bivariate
normal distribution with mean 0 and covariance matrix
from a bivariate
normal distribution with mean 0 and covariance matrix 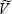 , such that
, such that 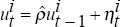 ,
where
,
where 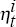 are independent and identically distributed;
are independent and identically distributed;
-
generate sequences of synthetic data
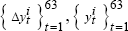 using
using 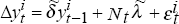 and
and 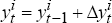 , where
, where 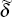 and
and 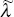 are from the IV
estimation using the original data;
are from the IV
estimation using the original data;
-
generate a sequence of synthetic data
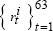 according to
according to 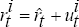 .
Re-estimate Equation (A4) by OLS using
.
Re-estimate Equation (A4) by OLS using 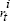 instead of rt
and obtain a new set of fitted values,
instead of rt
and obtain a new set of fitted values, 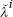 ;
;
-
estimate the equation
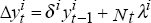 by IV, using
by IV, using 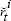 as an instrument
for rt, and hence generate parameter estimates
as an instrument
for rt, and hence generate parameter estimates 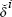 and
and 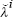 ;
and
;
and
-
with the parameter estimates
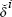 and
and 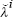 , use Equation (A3)
to calculate, for this ith iteration, the effect of
a one per cent rise in the real interest rate on the year-ended growth rate
of output,
, use Equation (A3)
to calculate, for this ith iteration, the effect of
a one per cent rise in the real interest rate on the year-ended growth rate
of output, 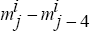 , after j quarters.
, after j quarters.
The figures in the text show the 5th, 50th and 95th percentile values for the year-ended growth rates.
A.3 Recursive Regressions
For the recursive regressions, a new Monte Carlo distribution is estimated from 1,000 trials after each new quarter of data is added.