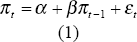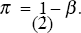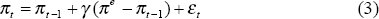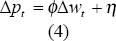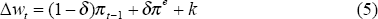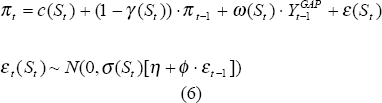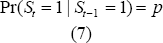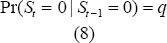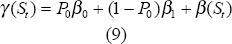RDP 9611: A Markov-Switching Model of Inflation in Australia 3. Model Specification

The starting point for the model used in this paper is a simple autoregressive model of inflation as used in earlier studies:^[4]

where π_t is the inflation rate. Apart from the simplicity of the specification the framework is also appealing as it can capture inflation expectations effects. The long-run mean value of inflation in equation (1) is simply:

This might also be thought of as a central inflation expectation. Then, if we set γ = 1 − β, a simple rearrangement of equation (1) into a partial adjustment framework highlights the importance of inflation expectations:

where π^e is the expectation of the average inflation rate as defined in Equation (2). If people expect inflation to return quickly to its expected value then γ will be high (putting price setting frictions to one side). If, however, people do not have firmly anchored expectations γ will tend to be low. The extreme of this situation is when expectations have no long-run anchor, and hence γ = 0 and inflation behaves as a random walk.

One justification for this interpretation is that it captures the effects of wage demands on costs. If wage increases lead to price increases through a simple markup model such that:

and wage demands are based upon expected inflation as given in equation (5):

we can see how inflation expectations should affect inflation. In equations (4) and (5) η and k are constants that capture the influence of other variables on prices and wages; for example, k should capture productivity effects. If people have a firmly fixed inflation expectation then δ should be close to 1. If, however, they do not have a firmly fixed expectation, then wage claims are likely to have a stronger autoregressive element with δ close to 0. Reducing equations (4) and (5) yields Δp_t = (ϕδπ^e + ϕk + η) + ϕ(1 − δ)π_t−1 which is exactly the same form as Equation (1). Within this setup δ, which reflects expectations, has a direct analogue in Equation (1) as the autoregressive coefficient.

The foregoing captures the central conceptual reason for regime changes within this paper – that inflation expectations change, possibly reflecting changes in policy objectives or in the nature of shocks hitting the system. As expectations change, the autoregressive parameter in the above model will change. This paper identifies periods with differing autoregressive parameters as coming from differing regimes. Following on from this discussion we specify the general model used in this paper in Equation (6) based on the general form of Equation (1):

where π_t is the quarterly underlying inflation rate, S_t is the state variable (either 0 or 1), 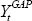is the output gap and ε_t is an ARCH process with a state-dependent scaling term, σ(S_t). The state variable is assumed to evolve following a standard Markov process as described in equations (7) and (8):

3.1 Why This Form?

The form chosen is a slight modification of standard univariate models of inflation used in previous applications of the Markov-switching methodology. An output gap is included to improve the model by including a significant exogenous explanator, and the ARCH process is included to capture information on the nature of inflation uncertainty.

The inclusion of both a scaling term for the error and an ARCH process allows for the separate identification of the reasons that errors would vary over time. A significant scaling term would suggest that high inflation periods were associated with higher volatility and, thus, that variability about the mean of the current regime was proportional to the level of that mean. A significant ARCH term would seem more indicative of regime uncertainty. That is, people would be unable to identify if a particular shock was an example of random fluctuation or a change in regime.

3.2 Learning

When regime switches are considered, one question that can be asked is whether people recognise the changes when they occur and modify their behaviour accordingly. That is, how quickly do people learn about regime changes? To add to the structure of the model and allow for a more flexible fitting of the data, a specific learning process is introduced. This is implemented by imposing:

where P₀ is the estimate of the probability of being in state zero at time t and β_i is the value of β in state 0 or 1. In this context β can be interpreted as the underlying nature of the regime and the probability weighted terms as the expectational effect. Thus, as the transition from one state to another occurs, more and more people learn about the true regime and adjust their price setting accordingly. Thus, if a regime change occurs (and β(S_t) changes), yet no one recognises it, the autoregressive parameter will move less than when a change occurs that everyone recognises. Thus, the probability estimate generated by the model is also used as an estimate of the proportion of people who recognise the regime change. This allows the autoregressive parameter on the inflation process to adjust smoothly between the two states, rather than in a discrete fashion. This should also allow the model to accommodate some intermediate inflation state (where the probability of being in either state is around 50 per cent). This is most useful for forecasting if we believe that periods of intermediate inflation and regime uncertainty are possible.

One technical identification problem is introduced by the learning regime. The model could find it hard to distinguish between an inflation process with a low autoregressive parameter that has a low probability of occurrence and a regime with a higher autoregressive parameter that has a high probability. Nonetheless, this is only a problem at an instant in time. Given a longer history of observations and the fact that maximum likelihood techniques are used, the model identifies the most likely regimes which will, consequently, have a high estimated probability of occurrence.

Footnote

For example, Evans and Wachtel (1993) and Laxton, Ricketts and Rose (1994). [4]