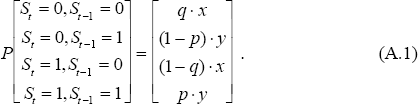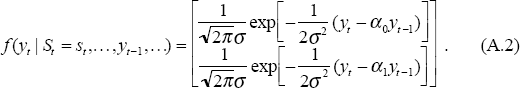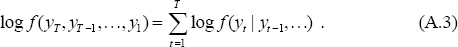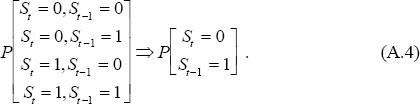RDP 9611: A Markov-Switching Model of Inflation in Australia Appendix A: The Hamilton Filter and Maximum Likelihood Estimation

The estimation method used in this paper makes use of the algorithm described by Hamilton (1989).^[13] The section below provides a brief description of the procedure. For technical details, please refer to the paper by Hamilton.

The Hamilton filter is an iterative procedure which provides estimates of the probability that a given state is prevailing at each point in time given its previous history. These estimates are dependent upon the parameter values given to the filter. A by-product of this process is the likelihood function for the given parameter estimates. Running the filter through the entire data, provides a log likelihood value for the particular set of estimates used. This filter is then repeated to optimise the log likelihood to obtain the MLE estimates of the parameters. With the maximum likelihood parameters, the probability of state 0 at each point in time is calculated and these are the probabilities that are reported in the paper.

The Hamilton Filter

The Hamilton filter starts with a vector of estimates of the probability that a particular sequence of states has led to period t−1. That is, it starts with a 2^r × 1 vector P[S_t−1 = s_t−1, S_t−2 = s_t−2,…,S_t−r = s_t−r | y_t−1, y_t−2,…], where r is the length of the path. The length that it is necessary to keep track of is dependent upon the specification of the model dynamics. For example, in Hamilton's paper it is necessary to keep track of the past four states as he specifies a fourth order moving average process. In this paper it is only necessary to keep track of the past two states as a first order ARCH process is being used. From this vector, the probability that S_t = s_t is calculated by making use of the Markov-switching probability estimates. Thus, if P[S_t−1 = 0 S_t−1 = 1] = [x y] then:

The next step is to calculate the likelihood that y_t occurs given the previous path of states and variables. That is, evaluate the value of the normal distribution at the point given by the residual. Consider, for example, the simple autoregressive model:

Here the top element of the matrix is the likelihood in state 0 and the bottom element is the likelihood in state 1 (the difference is in the alpha parameter). This is then multiplied by the probability estimate (A.1) to give the joint conditional density distribution of y_t and (S_t, S_t−1,…). The overall likelihood of y_t, f(y_t | y_t−1,…), is just the sum over all possible state paths of the joint conditional density function. That is, the probability-weighted likelihood for all possible paths. This is saved and used in calculating the likelihood of a particular set of estimates. This is:

To generate the estimate of the probability that various paths lead to period t, P[S_t = s_t,S_t−1 = s_t−1,…,S_t−r = s_t−r | y_t,y_t−1,…], divide the conditional likelihood for each path by the total likelihood for all the paths. To obtain the input for the next iteration of the filter, collapse the probability matrix by summing over the possible states at time t−r. Thus, for example:

This can then be used to run through the filter to get estimates for t+1 and so on. At each point in time the estimate of the probability that the current state is 0, given information available up to that time, is obtained by summing the probability vector in the same way as is illustrated in (A.4).

Footnote

The procedure was coded in GAUSS based on a program obtained from Thomas Goodwin, Claremont Graduate School. [13]