RDP 9512: Consumption, Investment and International Linkages 4. Results
December 1995
- Download the Paper 172KB
4.1 Consumption
The consumption equation (7) is estimated using quarterly data. Domestic consumption and output are expressed in per capita terms, although foreign output is not – intuitively it is clear that any information contained in an innovation to foreign output is adequately gleaned from the aggregate quantity. As discussed in detail in Appendix B of McKibbin and Richards (1988), a true measure of consumption[12] – one that includes the flow of services provided by the accumulated stock of durables – is required. The technique used to generate this flow measure follows McKibbin and Richards (1988) and is outlined in Appendix B.
The instruments used for domestic disposable income growth in the estimation procedure include lagged domestic real cash rates, consumption growth and the level and growth of domestic income. Foreign output, in levels and differences, is also considered. A cointegrating relationship between domestic and foreign activity levels is allowed for in one of the specifications. The inclusion of an error correction term, involving domestic consumption and income, was also considered. However, the presence of a cointegrating relationship was not established using the Engle and Granger two step method and further, its inclusion generally proved insignificant.
The model is estimated for the sample period 1973:Q2–1994:Q4 and also for the sub-periods 1973:Q2–1982:Q4 and 1983:Q1–1994:Q4, in order to identify any changes in the degree of liquidity constraints. OECD, US and Japanese output measures are considered.
The results from estimating equation (7) are given in Tables 2 and 3. Table 2 comprises three distinct parts: each part uses different foreign activity measures in the consumption model. Columns 1, 3, and 5 of Table 2 contain the R2 highlighting the ability of the specified instrument set to explain real household disposable income.[13] The results show that the instrument set including a foreign activity measure provides the superior explanation of household income.[14] Consequently, the standard errors for the point estimates also tend to be smaller for these models. Of these, the preferred model is a variant of the GS equation, excluding the Southern Oscillation Index and incorporating differing lag structures for interest rates, domestic output and foreign output. For OECD and US activity measures, the GS equation explains about 55 per cent of the variation in real household disposable income per capita over the period 1983:Q1–1994:Q4, supporting the results presented in GS for real GDP. The use of Japanese output as the foreign output measure in the preferred instrument set reduced the R2 to 0.47. Additionally, the preferred GS equation provides a substantially better set of instruments than those proposed by McKibbin and Richards (1988).
| 1973:Q2–1982:Q4 | 1983:Q1–1994:Q4 | 1973:Q2–1994:Q4 | ||||
|---|---|---|---|---|---|---|
| R2 | 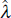 |
R2 | 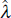 |
R2 | 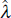 |
|
| Instruments | (1) | (2) | (3) | (4) | (5) | (6) |
| OECD | ||||||
| ΔYd | 0.25 |
0.45** (0.21) |
0.18 |
0.11 (0.14) |
0.14 |
0.22 (0.14) |
| ΔYd,ΔC | 0.32 |
0.67** (0.20) |
0.19 |
0.03 (0.14) |
0.16 |
0.22* (0.13) |
| ΔYd,r | 0.31 |
0.44** (0.18) |
0.34 |
0.21** (0.10) |
0.17 |
0.23* (0.12) |
| ΔYd,ΔYf,Yd,Yf,r | 0.56 |
0.37** (0.12) |
0.51 |
0.20** (0.08) |
0.37 |
0.23** (0.08) |
| US | ||||||
| ΔYd | 0.25 |
0.47** (0.21) |
0.15 |
0.05 (0.16) |
0.14 |
0.21 (0.14) |
| ΔYd,ΔC | 0.33 |
0.67** (0.19) |
0.17 |
−0.03 (0.16) |
0.16 |
0.21 (0.13) |
| ΔYd,r | 0.31 |
0.49** (0.18) |
0.33 |
0.21** (0.10) |
0.17 |
0.23* (0.12) |
| ΔYd,ΔYf,Yd,Yf,r | 0.53 |
0.43** (0.12) |
0.54 |
0.20** (0.08) |
0.36 |
0.25** (0.08) |
| Japan | ||||||
| ΔYd | 0.23 |
0.39** (0.19) |
0.14 |
0.09 (0.15) |
0.14 |
0.21 (0.13) |
| ΔYd,ΔC | 0.31 |
0.58** (0.18) |
0.18 |
0.02 (0.14) |
0.15 |
0.22* (0.12) |
| ΔYd,r | 0.28 |
0.45** (0.17) |
0.35 |
0.25** (0.10) |
0.16 |
0.22* (0.12) |
| ΔYd,ΔYf,Yd,Yf,r | 0.54 |
0.34** (0.11) |
0.47 |
0.23** (0.08) |
0.36 |
0.23** (0.08) |
Notes: (a) Subscripts d and f denote domestic real disposable income
and foreign GDP respectively. |
||||||
| Instruments | 1973:Q2–1982:Q4 | 1983:Q1–1994:Q4 | 1973:Q2–1994:Q4 |
|---|---|---|---|
| OECD | |||
| ΔYd | 0.31 | 0.25 | 0.45 |
| ΔYd,ΔC | 0.12 | 0.23 | 0.44 |
| ΔYd,r | 0.30 | 0.31 | 0.42 |
| ΔYd,ΔYf,Yd,Yf,r | 0.34 | 0.30 | 0.40 |
| US | |||
| ΔYd | 0.15 | 0.85 | 0.59 |
| ΔYd,ΔC | 0.05 | 0.89 | 0.58 |
| ΔYd,r | 0.11 | 0.77 | 0.54 |
| ΔYd,ΔYf,Yd,Yf,r | 0.11 | 0.77 | 0.48 |
| Japan | |||
| ΔYd | 0.84 | 0.04 | 0.42 |
| ΔYd,ΔC | 0.80 | 0.05 | 0.41 |
| ΔYd,r | 0.95 | 0.06 | 0.40 |
| ΔYd,ΔYf,Yd,Yf,r | 0.73 | 0.06 | 0.39 |
It is worth noting an empirical curiosity that arises when using the GS equation to estimate real household disposable income. The striking result of GS is the strength of the contemporaneous relationship between Australian and foreign output growth. However, for the OECD and US models, there is a negative coefficient on the contemporaneous foreign growth term when disposable income growth is regressed on the GS explanators. This is somewhat surprising given that disposable income and gross domestic product are highly correlated. Irrespective, our principal concern is the identification of suitable instruments – the GS equation is clearly adequate for this purpose.
The remaining columns detail the point estimates of λ with standard errors in brackets. All twelve regressions reported in Table 2 show a decline in the point estimate over the two sub-samples. Formal tests of a decline in λ show weak evidence of declining sensitivity of consumption to current income (see Appendix D).
The decline in the point estimates potentially captures the effect of financial deregulation in reducing liquidity constraints encountered by some portion of the economy. The estimates can be interpreted as suggesting that the proportion of current income (liquidity constrained) consumers has decreased from 40–45 per cent in the 1970s to 20–25 per cent in the 1980–90s. Blundell-Wignall, Browne and Tarditi (1995) present results for the pre and post financial deregulation periods (the 1960–70s and the 1980–90s) for a number of OECD countries. They find a similar decline in the sensitivity of consumption to current income for the majority of countries studied. However, they did not find such a result for Australia. We established that the difference in findings is due to the extended sample period in the deregulated environment available for the analysis presented here.
Table 3 provides results for the role of foreign activity as an indicator of permanent income. In particular, the significance levels (p-value) of γ, the foreign variable coefficient in the estimated model indicate whether there is a direct influence of foreign activity levels on consumption decisions.
The results show that innovations in OECD output are not statistically significant determinants of current consumption. When US output is used, one instrument set yields a significant coefficient value on US output growth at the 5 per cent level over the 1973:Q1–1982:Q4 sub-period with two other instrument sets providing significant results at the 11 per cent level. The latter period yields no significant results. For the earlier period a coefficient value of 0.2 was estimated for the growth of US output when the preferred instrument set was used.
A rationalisation for the changing US influence is that the 1970s was to some degree a period of greater economic uncertainty, placing increased importance on new information in forming consumption decisions. Hence, knowledge of the contemporaneous change in foreign output is an influential determinant of consumption due to its perceived implications for domestic income levels. In the 1980s though, it could perhaps be argued that a more stable economic environment implied recent developments in foreign output provided little information about changes in domestic permanent income.
However, given the documented strength of the relationship between the contemporaneous growth rates of Australia and the US or OECD, particularly in the latter period, the specification may suffer from multicollinearity. This tends to bias results against establishing significant point estimates for the coefficient on foreign output growth, and hence, may explain the failure of the model to identify a significant foreign influence.
Lastly, the results for Japan show that innovations in Japanese activity provide substantial information about Australian permanent income. For the sub-period 1983:Q1–1994:Q4 all models give a significant coefficient on the contemporaneous growth coefficient at the 6 per cent level, while in the former period all coefficients are insignificant. Over the latter period the coefficient on Japanese activity growth is 0.3. A possible rationale for the differing sub-period results is that over the sample period, the average consumer has become increasingly aware of the importance of Japan as an Australian export market. Thus improved Japanese economic performance, leading to increased domestic export revenues, may be perceived as an increment to permanent income.
The preceding results are based on the assumption that the market rate of interest is constant (and equal to the rate of time preference). If this assumption is relaxed, then the appropriate specification also includes the real interest rate. However, the inclusion of contemporaneous real cash rates proved insignificant. The real five and ten year treasury bond yields were also considered but again proved to be insignificant.
4.2 Investment
The investment equations are estimated over the period 1980:Q1–1994:Q3 using quarterly data. Two measures of the capital stock were used. Firstly, the ABS measures of the annual capital stock were interpolated to give a quarterly series. Secondly, the theory behind the investment equation described in Section 3 implies that not all of gross investment results in increases in the capital stock as some is used up in transforming goods into capital. Consequently, a measure of the capital stock was calculated using equations (8) and (10). This requires an estimate of the parameter T. Whereas McKibbin and Siegloff (1987) use three different values of T (10, 20 and 30), the value of T used here is 15. Separate cost-adjusted series were calculated for non-dwelling construction and equipment investment due to the availability of depreciation estimates for each component. Note that varying T also changes the value of Q.
The model is estimated in log levels. The cash flow to capital stock ratio and the investment to capital stock ratio were tested for non-stationarity. The cash flow to capital stock series clearly rejects the presence of a unit root though the ADF tests were not as decisive for the investment to capital stock series. However, observing the data indicates the series has appeared to fluctuate around two means over the period 1960:Q3 to 1994:Q3 – a shift to a lower investment stock ratio occurring around the time of the first oil shock. This observation, coupled with the knowledge that the ratio is necessarily bounded, suggests that estimation in levels is appropriate.
To obtain a suitable investment equation several variations of equation (14) are considered. Results for all models are presented in Table 4.
| Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| Cash flow | 0.19 (0.13) |
0.18 (0.13) |
0.21** (0.05) |
0.22** (0.05) |
0.19** (0.07) |
0.04 (0.07) |
0.18** (0.07) |
0.08 {0.00} |
0.13 {0.00} |
| Q | −0.05 (0.07) |
||||||||
| Q(−1) | −0.01 (0.07) |
0.02 (0.03) |
0.05 (0.05) |
0.02 (0.03) |
0.01 (0.06) |
||||
| I/K(−1) | 0.90** (0.05) |
0.91** (0.06) |
0.88** (0.06) |
0.64** (0.10) |
0.89** (0.06) |
0.87** (0.07) |
|||
| Sales | −0.03 (0.10) |
||||||||
| Confidence | 0.00005* {0.09} |
||||||||
| Capacity utilisation | 0.0018** (0.0006) |
||||||||
| Credit | −0.01 (0.02) |
||||||||
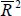 |
0.01 | 0.00 | 0.84 | 0.84 | 0.85 | 0.86 | 0.84 | 0.84 | 0.31 |
Notes: (a) Numbers in parentheses () are standard errors. Numbers in
brackets {} are F-statistics derived from joint significance tests. |
|||||||||
Estimated models for the basic framework, allowing for differences in the time at which information captured by Q is available, are given in columns (1) and (2). As discussed above the specification with the lagged value of Q is preferable given that investment flows in a given quarter will generally be based on information available at the commencement of that period. However, results indicate that both models possess negligible explanatory power and that the time at which information becomes available is not important. A large number of studies have noted difficulty in establishing the empirical significance of Q. Various rationalisations for its low explanatory power have been cited with most related to the disparity between the market assessment of firms and the firms own internal assessments.
Column (3) allows for the ‘time to build’ aspect of investment. Contemporaneous cash flows and the lagged dependent variable enter significantly with Q remaining an insignificant explanator.
Given the empirical inadequacy of Q, three other variables are considered that may provide suitable proxies for the information Q theoretically embodies: retail trade (sales), business confidence and a capacity utilisation measure. Of these, business confidence most closely resembles Q, and probably provides a better measure of the firm's own internal assessment of its investment prospects. However, sales and capacity utilisation provide an indication of the state of the cycle, firm performance and the productivity of future investment and hence seem sensible candidates.
Columns (4), (5) and (6) present results for the specification when Q is replaced by these alternative measures. Retail trade, lagged one period, enters negatively and insignificantly. The business confidence measure was allowed to enter with two lags. The second lag of the confidence measures was included because a comparison of its time series relative to that for business fixed investment suggests that business confidence leads investment expenditure by more than a quarter. The results show that the average contribution of business sentiment is positive and significant (at the 10 per cent level).[15] Contemporaneous cash flows and the lagged dependent variable also remain significant.
The last variable to be introduced in lieu of Q is capacity utilisation. While it enters as a significant explanator it seems that capacity utilisation and cash flows are highly collinear. The coefficient on cash flows becomes insignificant when capacity utilisation measure is introduced. The existence of a strong relationship is reasonable as both provide similar information. Both are adequate indicators of the economic cycle and both have informational content with regard to future returns to investment, although the cash flow variable should better capture the financial aspect.
While the Q-related variables do not appear to be good explanators of investment, the significance of the cash flow term lends support to the cash flow theories of investment. The results suggest that cash flow constraints do matter for firms. Instrumental variables estimation of the effect of cash flow yield similar results. Another variable that captures the health of a firm's balance sheets is the level of indebtedness, measured here by business credit. Model (7) shows that the point estimate is of the expected negative sign but is insignificant.
The remaining two models include lags of the cash flow variable with model (9) excluding the lagged dependent variable. Contrasting the results for model (8) against model (3) indicates that adding two lags of cash flow adds little predictive power and fails to alter the contribution of cash flows to investment expenditure. Model (9) shows that in the absence of the lagged dependent variable the addition of cash flow lags improves the model substantially over the basic model given by (2). However, in the light of the results in (8), it is clear that the lagged dependent variable captures all information provided by lagged cash flows.
As mentioned in the introduction to this section an alternative investment series implied by the neo-classical model was also used in the estimation procedure. Appendix E shows that the use of the cost-of-investment-adjusted series makes no substantial difference to the general results.
In view of the preceding discussion, models (3) and (5) provide suitable specifications of the investment equation with which to analyse the influence of foreign variables. The foreign influences considered are OECD and US contemporaneous output growth, US business fixed investment growth, the Dow Jones share price index, and US ten year bond rates.
Table 5 contains the estimates (using model 3) of γ, the coefficient on the foreign variable in equation (15) and the associated standard errors. None of the variables enter significantly and only one variable carries the expected sign. The analysis suggests that there does not appear to be a direct link between foreign economic outcomes and the level of domestic business fixed capital investment.
| Foreign variable |
US GDP growth |
OECD GDP growth |
US investment growth (lagged) |
US share price (lagged) |
Lagged real US bond rates |
Japan share price (lagged) |
|---|---|---|---|---|---|---|
| Coeff | −0.65 | 0.12 | −0.37 | −0.0013 | −0.0003 | 0.0006 |
| (s.e) | (0.84) | (1.41) | (0.33) | (0.0010) | (0.0026) | (0.0009) |
Finally, of all the variables considered in the investment equation, business confidence is the most likely to be influenced directly by foreign economic conditions. Consequently we estimate a business confidence equation and as previously, test for the inclusion of foreign variables. The domestic real cash rate and the contemporaneous and lagged domestic output growth rate are included as explanators. This is to control for the effects of domestic monetary policy on financial conditions and the relative profitability of investment and the stage of the economic cycle. Using this specification as a base regression, foreign variables are then included.
Table 6 contains the results of this estimation over the period 1980:Q1–1994:Q3, and highlights some interesting results. While the contemporaneous growth in US and OECD activity enter insignificantly, growth in US business fixed investment and the levels of various financial indicators are significant explanators. The real Fed Funds rate and the growth in US business fixed expenditure are significant at the 5 per cent level and real quarterly growth in the Dow Jones Index significant at the 10 per cent level. The real quarterly growth in the Nikkei index is also significant though enters with a negative sign. This result is surprising given that the business confidence and the Nikkei real quarterly growth series have a simple correlation coefficient of 0.04 and that theoretical priors suggest the relationship should be positive.
| Foreign variable |
US GDP growth |
OECD GDP growth |
US investment growth |
US share price |
Real US bond rate |
Real US Fed funds rate |
Japan share price |
|---|---|---|---|---|---|---|---|
| Coeff | 190.15 | −45.28 | 339.04** | 0.69* | −1.17 | −2.68** | −0.57* |
| (s.e) | (368.53) | (647.59) | (145.50) | (0.39) | (1.12) | (1.07) | (0.32) |
Notes: Values marked ** (*) are significant at the 5% (10%) respectively. |
|||||||
Hence, we have identified one channel of influence of foreign developments. However, column 5 in Table 6 shows that the effect of changes in business confidence on investment is small in magnitude.[16] Further, business confidence enters the specification with several lags rather than contemporaneously.
Footnotes
The national accounts measure of consumption was also used in the estimation procedure. Appendix C details results. [12]
The size of the R2 of the regression of the endogenous variable on the instruments is not necessarily the ideal measure of the usefulness of the instrument set. Good explanatory power of the instruments may be associated with higher endogeneity, thus reducing their value. See Hall, Rudebusch and Wilcox (1994). [13]
Several variants of the GS type instrument set were used in the estimation procedure that are not reported. All provided superior explanatory power to models not including foreign activity. [14]
A model including only the second lag of business confidence was also estimated giving a coefficient estimate of 0.00035. However, the coefficient is only significant at the 15 per cent level. [15]
The immediate effect of a ten percentage point change in business confidence is a 0.1 percentage point change in the ratio of investment flows to stock. Allowing for the strong auto-regressive nature of the specification a 0.83 percentage point change in the ratio of investment flows to stock results in the long run. [16]