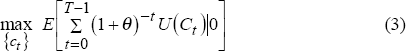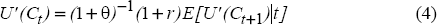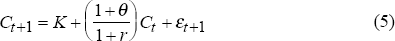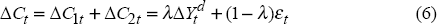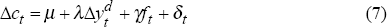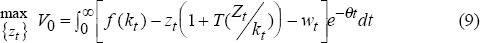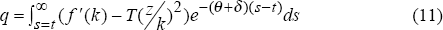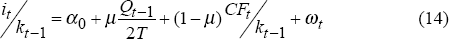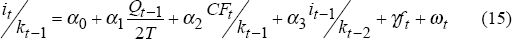RDP 9512: Consumption, Investment and International Linkages 3. The Models

3.1 Consumption

Our consumption model is based on that in Campbell and Mankiw (1989), which in turn is derived from Hall (1978). The consumer chooses the path of consumption to maximise expected lifetime utility:

where θ is the rate of time preference and E[.|t] denotes expectation conditional on information at time t.

The consumer is subject to the budget constraint A_t+1 = (A_t + L_t − C_t)(1 + r) where A is financial wealth and L is labour income.

The solution to this maximisation problem yields the following first order condition:

Intuitively this first order condition means that the consumer is indifferent between a small increase in consumption today rather than saving the increase and consuming it tomorrow.

If we assume that the utility function is quadratic, then the first order condition implies:

where K is a constant that reflects parameters in the utility function and the ratio of the discount rate to the interest rate. The expectation of ε_t+1 at time t is zero. No other variable known to the consumer at time t should help predict consumption at time t+1, given C_t.

Campbell and Mankiw assume that the permanent income hypothesis does not apply to all consumers, because of the presence of liquidity constraints or myopia. Rather, there are two groups of consumers. The first group (a fraction λ of the population) are current income consumers, perhaps because of liquidity constraint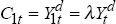s: where Y^d is disposable income. Thus .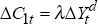

The second group are permanent income consumers: ΔC_2t = (1 − λ)ε_t where ε_t represents innovations to permanent income.^[8] Consequently aggregate consumption can be written:

ε_t represents any innovation to permanent income in time t. To introduce foreign influences into the consumption framework we assume that ε_t comprises two components. The first, δ_t, represents innovations in permanent income as in the traditional framework while the second, γf_t, captures that part of innovations to permanent income attributable to information provided by foreign variables. We assume that the foreign variables are orthogonal to the error term δ_t. Thus we will estimate the model (in per capita terms), allowing for a constant μ in the estimation procedure:

This equation allows us to test two different hypotheses. Firstly, if λ is significantly different from zero, then the permanent income hypothesis cannot be accepted.^[9] More particularly, one can interpret λ as the proportion of liquidity constrained consumers, and one can examine whether this has declined over time as one might expect given financial deregulation.

Secondly, the hypothesis that movements in foreign variables at time t represent news about permanent income can be tested. If the coefficient estimate, γ, on the foreign variable f, proves significant, then the model provides evidence of the existence of an international linkage through a consumption channel. Thus the model allows us to test whether foreign variables have a direct effect on consumption controlling for the indirect effect operating through income Y. The mechanism providing the connection may be an expectational channel – the knowledge that the US economy is performing strongly, coupled with the apparently tight links between both economies in the previous decade, may induce an increase in consumption because of the perceived increment in permanent income.

Obstfeld (1994) estimates an equation similar to (7) although he excludes domestic income growth, in order to examine the degree of world capital market integration. He uses growth in world consumption as the foreign variable under the assumption that with integrated capital markets, idiosyncratic national risks can be diversified so that the correlation of international consumption should be high. Obstfeld finds that in general the correlation between domestic and foreign consumption is low, but has increased in the period 1972–88 from 1951–72. Bayoumi and MacDonald (1994) combine Obstfeld's specification with that of Campbell and Mankiw but their results suffer from a high degree of multicollinearity. Importantly, the interpretation of variations of the foreign income growth coefficient becomes difficult with the inclusion of foreign consumption growth as part of the dependent variable. In this paper we are attempting to isolate the influence of foreign variables on domestic permanent income. The Bayoumi and MacDonald (1994) specification not only captures this channel but also the offsetting channel of changing foreign liquidity constraints.

Finally, it is necessary to estimate the equation using instrumental variables. This is because innovations to current income are likely to be correlated with innovations to permanent income. Thus Δy_t is not orthogonal to δ_t, violating the assumptions of ordinary least squares. Therefore we use as instruments for Δy_t, variables which are correlated with Δy_t but not with δ_t.

3.2 Investment

The investment model combines a standard neoclassical model of investment with adjustment costs (based on Hayashi (1982)) with the recent literature emphasising the importance of cash flow in financing investment (see Fazzari, Hubbard and Petersen (1988)). This latter literature relies on theories of asymmetric information to argue that it may be more costly for a firm to raise funds for investment from external sources compared to internal finance.^[10] Consequently, similarly to liquidity-constrained consumers, for some firms, current investment spending is ‘excessively sensitive’ to current cash flow.

The sensitivity of investment to cash flow is counter to the proposition of Modigliani and Miller (1958) which implies a separation between the real and financial decisions of the firm. However, Modigliani and Miller noted in their seminal article that their results assumed that firms had complete access to capital markets (see p. 296).

To derive the investment equation, assume that the cost of increasing the capital stock k by an amount z is given by:

i is the level of gross investment (all variables are in per capita terms) and it takes T() units to transform goods into capital. For simplicity we assume that T is constant so that the cost of adjustment is quadratic.

The firm maximises the present discounted value of future cash flow which is the value of output less wage and investment costs:

subject to the capital accumulation equation:

where w is the wage, δ is the depreciation rate, θ is the discount rate and f(k) is the production function (in per capita terms).

The solution to this problem yields the following two equations:^[11]

where q is the shadow price of investment and equals the present discounted value of the marginal product of capital less the cost of installing the capital; and:

That is, capital formation is positive when q>1. Writing this in terms of gross investment i (which is what we actually observe) gives:

As in the permanent income model of consumption we assume that a fraction μ of firms follow this neoclassical model of investment while a fraction (1−μ) either are unable to borrow externally or need to pay a premium on external borrowing and must fund their investment from current cash flow CF. The equations we estimate are then based on the following specification:

In estimating this equation, Q performs two separate roles. Firstly, it is the determinant of investment for firms which have complete access to capital markets. Secondly, for those firms which are constrained in the capital market, it controls for the fact that the cash flow variable may partly reflect information about future investment opportunities, in the same way that current income may be correlated with permanent income in the consumption equation.

The Q variable that we use is average Q rather than marginal Q which may reduce its ability to capture future investment prospects. Another problem with the Q variable is the fact that the very assumption of capital market imperfections implies that the firm's internal assessment of Q differs from the measurable market assessment. Hubbard and Kashyap (1992) also argue that Q may be an imprecise measure because of imperfect competition and non-constant returns to scale. Consequently, we try sales as a proxy for the future investment component of cash flow.

We use the lagged value of Q to reflect the investment opportunities at the beginning of the period. As with current income in the consumption equation, cash flow may be correlated with the error term. Consequently, we use lagged values of cash flow as instruments. An alternative approach is to use the end of period value of Q which should incorporate all news and productivity shocks that occurred during the period.

To capture the ‘time-to-build’ aspect of investment, we adopt two approaches. Firstly, we include the lagged dependent variable on the right-hand side. Secondly, we include lagged values of the cash flow variable.

As in the consumption equation, we introduce foreign variables to the right-hand side of this equation to determine if there is a contemporaneous linkage between the world and the Australian economy through investment. There are a number of potential channels for foreign variables to influence domestic investment. As in the consumption model it is reasonable to posit an expectational channel. This could operate through both real and financial factors. Alternatively, changes in foreign business fixed investment may actually reflect fluctuations in foreign direct investment in the domestic economy. This may directly be captured as higher domestic investment and also serve to boost domestic business sentiment. Lastly, with increasing financial integration developments in foreign assets may have important implications for domestic costs of finance.

Thus versions of the following equation are estimated with the significance of γ determining the influence of the foreign variables:

Footnotes

Note that we have assumed that the discount rate is equal to the interest rate in deriving this expression from equation (5). We relax this assumption in the empirical work. [8]

Campbell and Mankiw (1989) interpret the size of λ as the extent to which the permanent income hypothesis is approximately true. [9]

An earlier tradition explains the reliance on internal funds by the presence of transactions costs. [10]

The solution is presented in more detail in Appendix A. [11]