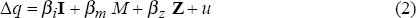RDP 9507: Macroeconomic Policies and Growth 4. Inflation and Growth
October 1995
- Download the Paper 184KB
‘Economic analysis of the costs of inflation – the mirror image of the benefits of price stability – is inevitably disappointing to the many ... who know that inflation is a deep societal problem. The question is whether what the many know is merely difficult to prove, or rather is substantially exaggerated’ (Fischer 1984, p. 33).
Given the crucial role of monetary policy in determining the inflation rate in the longer run, it is important when discussing macro-policies and growth, to understand the relationship between inflation and growth. This section examines this relationship.
Of the myriad ways in which inflation reduces economic efficiency (summarised, for example, by Fischer and Modigliani (1978) and Briault (1995)) there are three of particular relevance for economic growth. First, even anticipated inflation distorts the intertemporal allocation of resources as higher nominal interest rates interact with the tax system to affect saving and investment. Second, unanticipated inflation generates greater uncertainty about future inflation, discouraging long -term contracting and raising risk premia on interest rates, which in turn inhibits investment. Third, because higher inflation is associated with larger relative price variability, price signals become more difficult to interpret and the sectoral allocation of resources is adversely affected.
While theoretical calculations have been made of some of the costs of inflation, much discussion is based on simple intuition rather than explicit theoretical formulations. Despite increasingly sophisticated attempts (see, for example, Black, Macklem and Poloz (1994)) it is still very difficult to provide theoretical analysis of many of the economic consequences of inflation. Again quoting Fischer (1984, pp. 45–46), speaking with some exasperation at this lack of progress:
‘Surely inflation is associated with ... more weighty matters than money triangles and the efficiency of the price system.’
With theory providing little guidance on how the effects of inflation should be included in models of economic growth, most empirical studies simply add average inflation, and/or its standard deviation, to otherwise standard cross -country growth regressions. In discussing the evidence that emerges from these studies, we begin with the influential contributions of Levine and Renelt (1992) and Levine and Zervos (1993), henceforth LR and LZ.
In motivating their study, LR review the huge literature using cross -country regressions to search for empirical links between long -run growth and a variety of economic policy, political and institutional factors suggested by theory. They list 40 cross-sectional studies published between 1980 and 1990, each regressing the growth rate over a given period against a variety of variables. In all, over 50 variables have been found to be significant explanators of growth in at least one regression. As it is hard to believe that all these variables are important for growth, LR and LZ propose a strict test of the robustness of these regressions, based on Leamer's (1983) extreme bounds analysis.
LR and LZ consider regressions of the form:
where Δq is per capita GDP growth, I is a set of variables always included in the regression, M is the variable of interest and Z is a subset from a pool of variables identified in past studies as potentially important explanators of growth. Their analysis involves first running a ‘base’ regression including the I-variables on their own. Then the variable of interest, M, and all possible combinations of up to three Z-variables are added to the regression. If the coefficient estimate βm remains of the same sign and significant at a 0.05 level in all these regressions, then the variable M is described by LR and LZ as a ‘robust’ explanatory variable for economic growth. Alternatively, if the coefficient βm changes sign or becomes insignificant in any regression, M is a ‘fragile’ explanator for economic growth. As this description makes clear, this is a very strict test of the robustness of the variable, M, as an explanatory variable for economic growth.
LR and LZ differ in their choice of I-variables for their base regressions. Both studies include initial secondary school enrolment as a proxy for initial human capital. They both also include initial real GDP per capita to allow for ‘convergence’: the fact highlighted by Dowrick (1995) that, other things equal, poor countries grow faster than rich ones. The LR base regression also includes population growth and the average investment share of GDP while the LZ base regression includes the average number of revolutions and coups over the sample period.[21]
For the purpose of examining the empirical relationship between inflation and growth, both base regressions are of interest. Inflation may plausibly affect economic growth by both altering the level of investment as well as affecting the efficiency of resource allocation. Adding inflation to the LR base regression, therefore, tests whether inflation affects economic growth after controlling for the level of investment. Alternatively, adding inflation to the LZ base regression tests whether inflation affects growth including its effect on the level of investment as one of its channels of influence.
Both LR and LZ conclude that inflation is a fragile explanatory variable for economic growth. They both find that average inflation (or its standard deviation) makes a statistically insignificant contribution to their base regressions. It should be noted, however, that these conclusions are based on regressions for about one hundred countries with average annual inflation rates over their estimation period, 1960–89, ranging from less than 3 per cent (for Ethiopia!) to 474 per cent for Bolivia.
In this paper, we are interested in the relationship between inflation and growth for countries like Australia with similar (advanced) industrial structures, and with comparable rates of inflation. We therefore apply the LR-LZ approach to examine the empirical link between inflation and growth for OECD economies with comparable inflation rates. We repeat the LR-LZ approach as closely as possible, thereby limiting the problem of data-mining: that is, of choosing among a large number of theoretically plausible specifications, the one that provides the strongest support for the story one is trying to tell.
It is often argued that fully -anticipated inflation imposes less economic costs than uncertainty about future inflation, and hence that the variability of inflation may be a better summary measure of the effects of inflation on growth than the average inflation rate. However, as Figure 3 shows for the OECD, there is a close correlation between average inflation and the variability of inflation (as measured by the standard deviation of inflation).[22] As a consequence of this correlation, it is a daunting empirical task to identify the effect on growth of the level and variability of inflation separately. In the empirical exercise to follow, we limit our analysis to examining the relationship between growth and average inflation, recognising that some of the effect on growth of higher average inflation may be a consequence of the fact that high inflation is also more variable inflation.
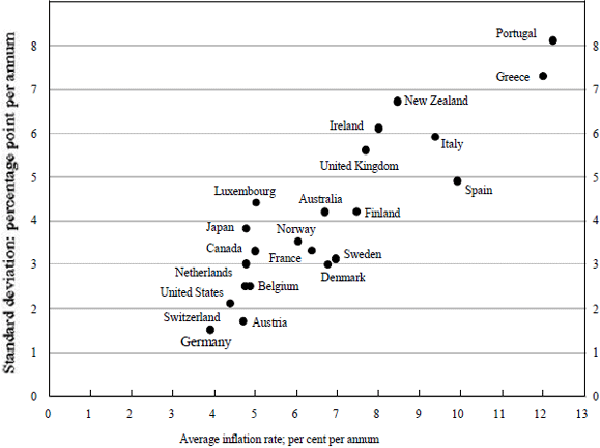
Figure 4 shows a scatter plot of the relationship between economic growth and average inflation for the 24 OECD countries over the period 1960–89. As previously mentioned, Iceland and Turkey are clear outliers, each with average annual inflation of 28 per cent, while the other 22 OECD countries had average annual inflation rates between 4 and 12 per cent (with Australian inflation averaging 7 per cent).
There is some evidence that the association between average inflation and growth weakens as inflation rises.[23] To minimise the influence of this effect on our regressions, we therefore exclude Iceland and Turkey from the analysis. (However, the Appendix reports regressions using the whole OECD sample.)
We now apply the LR-LZ approach to the 22 ‘low-inflation’ OECD countries rather than the hundred countries used by them. The dependent variable is always average annual per capita GDP growth, though the explanatory variables for the LR and LZ base regressions are different, as discussed above. After estimating the base regression, we add the variable of interest, the average inflation rate (measured using the GDP deflator), and then up to three Z-variables to the regression. The base regressions and Z-variables are reported in the Appendix while Table 6 summarises the coefficient estimates on inflation for all 30 regressions.[24]
| Coefficient on inflation in growth regressions | ||||||||
|---|---|---|---|---|---|---|---|---|
| Regression type |
Significant coefficients 5% |
Significant coefficients 10% |
Insiginificant coefficients |
Total |
||||
| No. |
Average | No. | Average | No. | Average | No. | Average | |
| value | value | value | value | |||||
| LR | −0.16 | 6 | −0.15 | 5 | −0.10 | 4 | −0.14 | 15 |
| LZ | −0.17 | 10 | −0.14 | 3 | −0.10 | 2 | −0.15 | 15 |
The estimated coefficient on inflation is negative for all thirty regressions (that is, higher inflation is associated with lower growth).[25] In about half the regressions, this negative estimate is statistically significant at a 5 per cent level, while in the other half, it is statistically insignificant. Using the definition introduced by LR and LZ, average inflation is, therefore, a fragile explanator of economic growth.
A possible shortcoming of this cross-country analysis arises from the effect of supply shocks. Adverse supply shocks reduce output and raise inflation leading to a negative correlation between inflation and growth even when higher inflation has not caused lower growth. The cross-country regressions reported in Table 6 may perhaps be picking up the fact that some industrial countries suffered worse aggregate supply shocks than others, and hence had both lower output growth and higher inflation over the estimation period. Since the obvious adverse supply shocks, OPEC I and II, affected inflation and growth after 1973, we split the sample in 1973 and examine the growth experiences 1960–73 and 1974–89 separately.[26]
Table 7 summarises coefficient estimates on inflation for the two sub -samples. As the table makes clear, coefficient estimates derived for the sub-samples are less statistically significant than for the whole sample. It is also clear that the coefficient estimates on inflation are usually smaller in magnitude when estimated over 1960–73 than over 1974–89 or over the whole sample, 1960–89. This supports the earlier suggestion that some of the negative correlation between inflation and growth over the whole sample arises from the differential impact of adverse supply shocks.[27]
| Coefficient on inflation in growth regressions | ||||||
|---|---|---|---|---|---|---|
| Regression type | Significant coefficients (10%) | Insignificant coefficients | Total | |||
| Average value | No. | Average value | No. | Average value | No. | |
| LR 60:73 | −0.04 | 11 | −0.08 | 4 | −0.05 | 15 |
| LZ 60:73 | −0.06 | 8 | — | — | −0.06 | 8(a) |
| LR 74:89 | — | — | −0.09 | 15 | −0.09 | 15 |
| LZ 74:89 | −0.10 | 7 | −0.11 | 1 | −0.10 | 8(a) |
|
Note: (a) One of the conditioning variables in the LZ regressions is not available for the sub-periods (see the Appendix). |
||||||
The overwhelming impression from the regressions reported in Tables 6 and 7 is that, after controlling for a range of other potentially relevant explanators, higher average inflation is correlated with lower average economic growth. Of the 76 regressions reported in the two tables, all but one give negative point estimates for the effect of inflation on growth. Furthermore, this conclusion should be of relevance for industrial countries like Australia since it is derived for OECD countries with average inflation rates less than 20 per cent per annum.
Not surprisingly, given the importance of the issue, the literature contains a large number of empirical studies estimating the effect of inflation on growth. Table 8 summarises the recent evidence, based primarily on cross-country studies for OECD economies in the 1960s, 1970s and 1980s. The table reports only the most relevant of the many regression specifications presented in each study. While the regressions reported are not all independent of each other, there is at least some variation in sample periods and in the explanatory variables used. Given the problems of adverse supply shocks discussed above, the table also reports some results for samples which end before OPEC I.
| Authors |
Period |
Model |
Sample |
Coefficient on average inflation | t-statistic (abs. value) |
|---|---|---|---|---|---|
| Grier and Tullock (1989)(a) | 1951–80 |
Panel |
24 OECD countries | 0.01 |
0.2 |
| Grimes (1991) | 1961–87 |
Panel |
21 OECD countries | −0.11 |
9.2 |
| Kyriakopoulos (1991) | 1960–88 |
Cross country | 24 OECD countries | −0.02 |
0.9 |
| Cozier and Selody (1992)(b) | 1960–85 |
Cross country | 22 OECD countries | −0.13 |
1.8 |
| Levine and Renelt (1992) | 1960–89 |
Cross country | Non-oil countries | −0.004 |
1.7 |
| Levine and Zervos (1993) | 1960–89 |
Cross country | Non-oil countries | −0.002 |
0.6 |
| Motley (1993) | 1960–88 |
Cross country | 22 OECD countries | −0.13 |
2.4 |
| Clark (1993) | 1960–85 |
Cross country | 22 OECD countries | −0.13 |
2.2 |
| 1960–88 | Panel | −0.08 | 1.9 | ||
| 1950–70 |
Cross country | |
−0.13 |
1.1 |
|
| Fischer (1993)(c) | 1961–88 | Panel | Non-oil | −0.13 | 2.0 |
| 1961–72 | Panel | countries | −0.20 | 3.4 | |
| Englander and Gurney (1994)(d) | 1960s–90 |
Panel |
19 OECD countries |
−0.06 |
1.6 |
| Barro (1995)(e) | 1960–90 |
Cross country | About 80 countries | −0.024 −0.016 |
4.9 0.5 |
|
Notes: (a) The reported regression also includes the standard deviation of
inflation, SDPI, with a statistically significant negative coefficient.
As PI and SDPI are highly correlated, the coefficient on PI
is very imprecisely estimated. |
|||||
As Table 8 makes clear, there is professional disagreement about the statistical significance of the relationship between inflation and growth. Some studies (for example Kyriakopoulos (1991), LR, LZ, Clark (1993) and Englander and Gurney (1994) conclude that the relationship between inflation and growth is either statistically insignificant at conventional levels of significance or fragile. Others (such as Grimes (1991), Cozier and Selody (1992), Fischer (1993) and Motley (1993)) argue that there is indeed a significant relationship, with higher inflation correlated with lower growth.
Despite this disagreement about statistical significance, it is striking that the vast majority of growth regressions in the literature report negative coefficient estimates on inflation. This is of course true of those studies that find a significant negative relationship between inflation and growth. It is also true, however, of the vast majority of studies that conclude that the relationship is statistically insignificant (see Table 8). For example, LZ report eight different specifications for their cross-country inflation-growth regressions. While the coefficient on inflation in these regressions is sometimes statistically significant and sometimes not – indeed, that is LZ's point – the coefficient is always negative.
While the results are not as robust as one would like, the most obvious interpretation of the evidence in Tables 6 to 8 is that the negative correlation between inflation and growth arises from a causal relationship. That is, other things equal, lower inflation leads to higher economic growth. (A possible alternative interpretation is that countries with low inflation also tend to have a range of growth-enhancing policies, due to a consensus about the benefits of economic growth. While the analysis attempts to control for the effect of other policies, one might argue that the measures it uses – budget surplus, ratio of trade to GDP, etc. – are too imprecise to capture the benefits of a general community commitment to growth.)
Nonetheless, accepting the interpretation that inflation has a causal impact on growth, it is worth quantifying the estimated gains from lower inflation implied by the point estimates in the tables. To do so, we assume a plausible value for per capita output growth (2 per cent per annum) and for the real interest rate used to discount future income (5 per cent per annum). Figure 5 then shows the cumulative gain in per capita output, discounted to the present, from reducing the inflation rate by one percentage point.
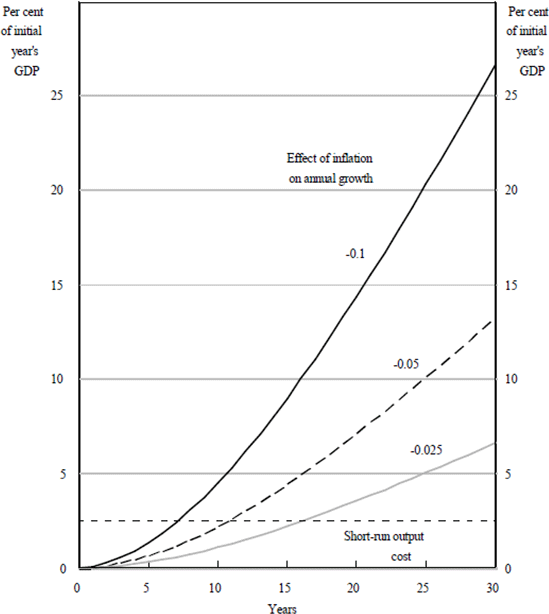
Results are presented for three alternative estimates of the effect of average inflation on annual growth (−0.025, −0.5 and −0.1), and the figure also shows Stevens' (1992) estimate of the short-run output cost of reducing inflation by one percentage point, 2.5 per cent of one year's GDP.
As Figure 5 shows, disinflation is an investment activity: the costs are borne at the time, while the gains accrue gradually and only outweigh the costs after an extended period. If the annual growth dividend from a one percentage point fall in inflation is as small as 0.025 – an estimate smaller in magnitude than most of the estimates in Tables 6 to 8 – it takes about 16 years for the discounted cumulated gains from faster growth to exceed the short-run output costs of achieving lower inflation (see Figure 5). However, even from such a small growth dividend, the cumulated gains from faster growth eventually exceed the short-run costs by a substantial margin. Of course, if the growth dividend from lower inflation is larger, the ‘breakeven’ point occurs earlier and the eventual gains from lower inflation dwarf the initial costs. Thus, while the estimates in Tables 6 to 8 are sometimes statistically insignificant, they are of considerable economic significance. Measured over an extended period, they imply substantial cumulated output gains from lower inflation.
To conclude, it is worth stressing that the available empirical evidence for industrial countries since World War II, is mute on the issue of whether there are gains from achieving zero or very low single-digit inflation. There are simply no data on economies operating with very low inflation for extended periods. The lowest annual inflation rate in the OECD over the 30 years, 1960–89, was achieved by Germany with a 4 per cent average. Over the shorter period, 1960–73, the lowest average annual inflation rate was in the United States, again with 4 per cent, while over the period, 1974–89, Japan had the lowest inflation with an annual average of 3 per cent. The effect on output growth of achieving average inflation below these rates is simply unknown.
Footnotes
Barro (1991) shows that the average number of revolutions and coups helps explain economic growth in a broad cross-section of countries. [21]
The figure is from Edey (1994). Iceland and Turkey have much higher and more variable inflation than the rest of the OECD and are not shown. As discussed in Briault (1995), a large standard deviation does not necessarily imply more uncertainty if the process generating inflation variability is known. However, alternative measures of uncertainty, constructed from surveys or econometric models, also show a close correlation with the average rate of inflation. [22]
See Fischer (1993) and Levine and Zervos (1993). Wright (1994) finds that while average inflation (PI) makes an insignificant negative contribution to growth in the LZ base regression, log(PI) makes a significant negative contribution – which also supports the point. By contrast, Barro (1995) argues that the relationship between growth and inflation is linear. [23]
The data are from the database used by King and Levine (1993) and were kindly supplied to us by Steve Dowrick. We use four Z-variables for both LR and LZ sets of regressions. Each set therefore includes one regression adding the average inflation rate to the base regression, four regressions adding one Z-variable to this regression, six adding two Z-variables, and four adding three Z-variables, for a total of 15 regressions. Estimation is by OLS with heteroscedasticity-consistent standard errors. A coefficient estimate of −0.1, for example, implies that a fall in average inflation of 1 percentage point is associated with a rise in per capita GDP growth of 0.1 percentage points per annum. [24]
This result seems in contrast with Figure 4 which suggests a slightly positive relationship between inflation and economic growth. This positive relationship occurs primarily because countries with low initial GDP tend to grow faster but also to have higher inflation. Controlling for initial GDP, the regressions suggest the relationship between inflation and growth is, in fact, negative. [25]
For consistency, in each sub-sample, we excluded from analysis all countries with an annual average inflation rate greater than 20 per cent. For the first sub-sample, 1960–73, all 24 OECD countries were included (Turkey and Iceland had average annual inflation rates of 11 and 16 per cent, respectively) while for the second, Iceland and Turkey were excluded. [26]
Another potential shortcoming of the analysis (suggested to us by John Quiggin) arises from possible mis-allocation of nominal GDP growth into real GDP growth and inflation (measured using the GDP deflator). For given nominal GDP growth, under-estimation of real GDP growth implies over-estimation of inflation and vice versa. If the extent and direction of mis-measurement is the same in each country, the analysis is not invalidated. If mis-measurement varies between countries, however, a spurious negative correlation is generated between measured growth and inflation. We therefore repeated the analysis using consumer price inflation which reduces this measurement problem. The coefficient estimates on CPI inflation are almost all negative and similar in magnitude to those reported in Tables 6 and 7. They are, however, much less statistically significant. [27]