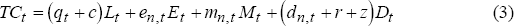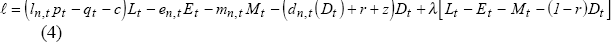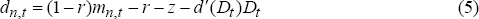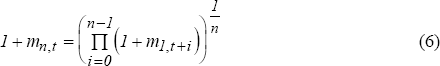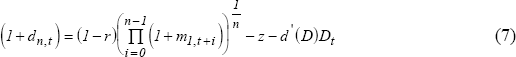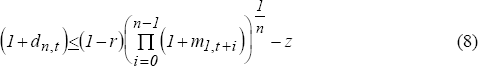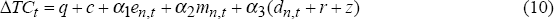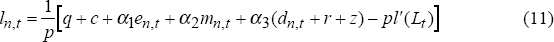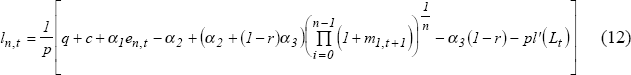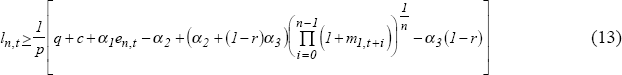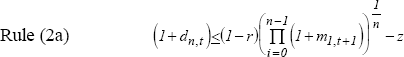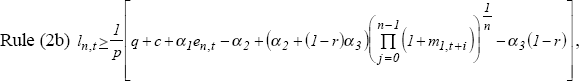RDP 9506: The Liberalisation and Integration of Domestic Financial Markets in Western Pacific Economies 4. Deposit and Loan Pricing Rules Under Fiat and Market Regimes

In order to identify how the relationship between the money market interest rate and institutional interest rates may have changed over time, it is necessary to have a benchmark model of the determination of institutional interest rates. This section outlines simple pricing rules for deposit rates and loan rates under both a fiat regime and a market regime, and so provides a perspective on the conditions under which changes in money market rates lead to changes in institutional rates. There is an extensive literature on banks and the pricing of their assets and liabilities – see, for example, Klein (1971), Monti (1972), Baltensperger (1980), Takeda (1985), Cottarelli and Kourelis (1994) and Borio and Fritz (1995). The model outlined in this paper, however, is constructed in a way which reflects to the main characteristics of banking in the region and focuses on both deposit and loan markets.

4.1 Fiat Deposits and Loan Rate Rules

When the deposit market is determined by the authorities, the deposit interest rate, d, is given by fiat:

When the loan market is determined by the authorities, the loan rate, l, is given by fiat:

The particular rule used by the authorities to set rates is not specified, since it will vary by country and by time, and it may or may not conform to the market rule outlined below.

4.2 Market Deposit and Loan Rate Rules

In this subsection, a model of institutional rate determination is constructed, the retail interest rate rules are stated, predictions of the rules for regression analysis outlined, and, finally, the model and rules are critically assessed. The deposit and loan rates are assumed to be determined by a profit maximising bank with a simplified balance sheet comprising reserves (R) and loans (L) on the asset side, and money market borrowings (M), deposits (D) and equity (E) on the liabilities side. It is assumed initially that these instruments are of the same maturity, n. Reserves are proportional to deposits, R = rD, where r is the reserves ratio, and it is assumed that reserves do not pay interest. Accordingly, the balance sheet constraint for the bank is:

Expected total profit is expected total revenue (TR) less expected total cost (TC) which are respectively,

where l_n,t, e_n,t, m_n,t and d_n,t are the rates of return at time t on the n-period instruments L, E, M and D respectively, p is the probability of payment of loan interest, q is the probability of default on the loan principal, c is the administrative cost of loans, and z is the administrative cost of deposits. It is assumed that the administrative costs on loans and deposits are constant and those on equity and money market borrowings are zero (equivalently, deposits are costlier to administer than equity and money market borrowings). Following Lowe (1995), the probabilities of interest payment and loan default are included since banks face asset risk in the sense that they must pay out deposits and deposit interest at par but are not guaranteed receiving loan principal and loan interest payments at par.

Banks may enjoy monopsony power in the determination of deposit interest rates, implying d=d(D) and d'(D)>0 since banks must increase the deposit rate to attract depositors, or monopoly power in the determination of loan rates, implying l=l(L) and l'(L)<0 since banks must reduce the loan rate to attract borrowers. Following the literature (Baltensperger 1980), it is assumed that banks are price-takers in the money market.

The deposit rate is determined through profit-maximising liabilities management by the bank. The Lagrangean may be written as:

Banks hold a proportion of their loans as equity for prudential purposes, and this is assumed to be a requirement imposed on them. Accordingly, banks maximise the Lagrangean with respect to M and D. The first order conditions imply:

Since banks only have price-fixing power in the deposit market, they take the money market rate as given. From equation (5), the deposit rate rises as the money market rate rises but falls as the reserve ratio, administrative costs and monopsony power of banks increase.

This specification assumes that money market instruments and deposits are of the same maturity but in practice this need not be so. The term structure is assumed to be defined in discrete time by the unbiased expectations hypothesis (Hicks 1946) and so the interest rate on the n–period money market instrument at time t, m_n,t, is:

where m₁ is the interest rate on a 1-period money market instrument. Adding 1 to both sides of equation (5) and substituting equation (6) for m_n, equation (5) may be rewritten as:

Given that d'(D)>0, this may be rewritten as:

If banks do not enjoy monopsony power in the deposit market then equation (8) holds as an equality.

This derivation assumes that depositors do not enjoy the same access to the money market as they do to the retail deposit market, for if they did and deposit rates were less than money market rates, they would place all their funds in the money market. The rejection of this arbitrage mechanism (and the consequent equalisation of money market and retail deposit rates) is made on the ground that most deposits fall below the minimum amount required for transacting in the wholesale market, thereby excluding depositors from the wholesale market and restricting them to the retail market. To the extent that arbitrage occurs (perhaps through non-bank financial intermediaries), the deposit rate will tend to equal the money market rate and the cost of reserves will be passed into the loan rate directly.

Now consider the loan rate. The loan rate is determined by profit maximisation, that is marginal revenue equal to marginal cost. Taking the total differential of equations (2) and (3), letting ΔL and L equal one, and setting the change in E, M and D equal to their share in L, α₁=E/L (which is determined exogenously to banks), α₂=M/L and α₃=(1−r)D/L, then:

Equating these and solving for the loan rate, yields:

Substituting equation (6) for the money market rate and equation (7) for the deposit rate (and assuming that the deposit market is competitive), the loan rate is given as:

where l_n,t is increasing in the probability of loan default, loan administration costs, the cost of equity, the cost of money market funds, the reserve ratio and market power, and is decreasing in the probability of payment of loan interest. This may be rewritten as:

which holds as an equality when banks do not have monopoly power in the loan market.

The deposit and loan rate rules may now be stated. Under the assumption of perfect foresight, the profit maximising bank sets the deposit rate in relation to its other, exogenously determined funding costs, specifically the cost of money market funds, according to the deposit pricing rule,

which is equation (8). The rule predicts that the deposit rate is less than or (at most) equal to the money market rate, and that the deposit rate is increasing in the money market rates expected to prevail over the deposit period and decreasing in both reserve requirements and net deposit administration costs. If the market for deposits is perfectly competitive, then Rule (2a) holds as an equality; otherwise banks can suppress deposit rates below the implied term structure equivalent rate.

When loans are priced in the market, the profit maximising bank sets the loan rate in relation to its funding and administration costs, the riskiness of its assets, and its market power according to the pricing rule:

which is equation (13). The rule predicts that the loan rate is greater than or (at least) equal to the money market rate, and that the loan rate increases when the cost of equity or money market borrowing increases, when the probability of loan default increases or the probability of interest payment falls, and when deposit reserve ratios increase. If markets are perfectly competitive, then Rule (2b) holds as an equality; otherwise banks can use market power to extract a higher loan rate than implied by funding and administration costs.

The rules indicate that institutional rates are functions of several variables, most of which are not observable or available, at least not on a monthly or even quarterly basis and usually not for a reasonable length of time.^[4] Accordingly, like Cottarelli and Kourelis (1994) and Borio and Fritz (1995), the analysis is restricted to regressing the institutional rate on the money market rate with the other factors appearing in the constant or error term.^[5] The rules are useful, however, in that they yield a number of predictions about the constant and slope coefficients.

Consider the constant term. When the deposit rate is the dependent variable, the constant term is expected to be weakly negative since, by Rule (2a), it is the negative of deposit administration costs. When the loan rate is the dependent variable, the model predicts that the constant will be weakly positive since it comprises loan administration costs, probabilities of default on loan principal and interest, and the cost of equity (or, more strictly speaking, the incremental cost of equity relative to borrowing in the money market). As these factors change, so will the constant term. Given that some banking systems in the region have at times experienced serious problems with non-performing or bad loans, one would anticipate that the constant term in the loan rate equation will vary over time.

The slope coefficient, on the other hand, is principally affected by regulation (that is, whether there is a regime shift from Rule (1) to Rule (2)), by the degree of competition in the banking sector, and by the nature of shocks to the term structure. As regulation, competition and the permanency of term structure shocks change, so will the slope coefficient. Given that banking systems in the region have been increasingly deregulated and competition has improved over time, one would anticipate that the slope coefficient will increase over time. The inclusion of the term structure implies a smoothing process according to which the effect of shocks to money market rates on deposit and loan rates will depend on their expected permanency. A rise in the slope coefficient may, therefore, merely reflect changes in the permanency and timing of shocks to money market interest rates, perhaps due to improvements in monetary management techniques or cyclical effects. To minimise this, the maturity of money, deposit and loan rates across countries should be as similar as possible and a sufficiently long sample selected.

The attraction of the rules is not just their simplicity but also their realism. In the first place, anecdotal evidence supports the claim that banks in fact use these sorts of rules in setting retail rates. Banks tend to set deposit rates with direct reference to money market rates, and they set loan rates on the basis of funding and administration costs and the riskiness of borrowers. In Japan, for example, banks price term deposit rates and the short-term prime rate off the CD rate (Bank of Japan 1994). In general, banks make as much use as possible of their market power in retail markets. Moreover, the rules capture key recent developments in deposit and loan markets in the Western Pacific region, namely regulatory regime shifts, increased competitiveness in the banking sector and occasional but significant changes in asset quality.

On the other hand, the model has some obvious short-comings. First, it assumes that financial institutions are price takers in the money market, but there are instances where this is violated. In Japan, for example, institutions which rely on call loans to fill a funds shortage sometimes borrow funds at above-market prices to allow institutions with a funds surplus to obtain extra profit.^[6] Even in the negotiable certificate of deposit (NCD) market, banks will sometimes limit issuance in order to push up rates to strengthen their bargaining position with borrowers (since the short-term prime rate is priced off the NCD interest rate).^[7] Similarly, in Thailand the number of players in the market is relatively small and prices at times have been subject to manipulation. While there are such examples of price-making in markets at various times, the approximation of perfect competition is not unreasonable. In Japan, for example, interbank rates generally closely follow open market developments, and CD rates very closely follow euroyen rates which are less subject to price-fixing (de Brouwer 1995). That is, banks have occasional but not systematic price-setting power in money markets, and this is certainly considerably less than the power they may have in institutional markets.

Second, the model assumes profit maximisation but this is not always the case in practice. For example, at various times banks in Australia, Indonesia and Japan, among other countries, have sought to maximise the size of their balance sheets rather than profits, and this is more likely to occur when central bank credit depends on the size of a bank's operations (Takeda 1985). Banks are also less likely to be profit maximisers when they are publicly owned (Cottarelli and Kourelis 1994). All else given, greater focus on balance sheet size implies higher deposit rates (Monti 1972) and lower loan rates, while less focus on profit maximisation implies slower adjustment of institutional rates (Cottarelli and Kourelis 1994). The effect on the price-setting rules depends on the extent to which the bank can ignore profit maximisation, but it is arguable that a policy of focussing on balance sheet size at the expense of profits is not sustainable over time, particularly in world markets which are increasingly integrated over time.

Third, the model is perhaps too simple. For instance, the intertemporal dimension is modelled in the term structure but not in the profit maximisation of the bank. If the bank is an intertemporal optimiser and possesses market power, then its strategic price rules may be considerably more complex and interesting. Another simplification is the modelling of the probability of default. If the probability of default is a function of the level or variance of the money market rate or the loan rate, of regime shifts, or of learning, then changes in asset quality may not appear just in the constant term but also in the slope coefficient. The model also does not take account of equilibrium risk-sharing or implicit contracting between the bank and its customer (Fried and Howitt 1980) according to which banks may price institutional rates such that they are less variable than they would be in spot markets in return for a higher average loan rate or lower average deposit rate. One way to do this in the model is to include utility functions of depositors and borrowers which are concave in income and costs respectively. Slope coefficients would also be a function of risk preference, and the results may indicate whether people had a preference for smoothing interest income over borrowing costs. Further modifications could include modelling the informal or curb loan market, modelling the different riskiness of borrowers in formal and informal markets, and modelling information asymmetries (as in Ahn (1994)). While these modifications would enrich the theoretical model and are worthy of pursuit, they are second order considerations in terms of the issues in this paper.

Footnotes

One possible alternative is to use proxies for the missing variables. For example, the effect of the risk of default on loan rates may be identified if economic growth is included (since risk of default is expected to be inverse to economic growth). This was tried without success for the Australian loan equation for all sub-samples by using the deviation from linear trend of the Melbourne Institute's index of manufacturing production. One problem with using these sorts of variables is that monthly observations of real variables tend to be highly volatile. Another is that a deterioration in economic conditions will reduce the demand for loans at any given interest rate, which may offset the putative rise in the loan rate due to a higher risk premium. [4]

If this approach is to yield consistent estimates, then the money rates must be uncorrelated with the unmodelled variables that appear in the error term. This may not be the case, if, for example, the risk of default is positively correlated with the money market rate. However, tests showed that the error term is not correlated with either the level or change in the money market rate. [5]

Based on interview in Tokyo, 27 February 1995. [6]

Based on interview in Tokyo, 20 February 1995. [7]