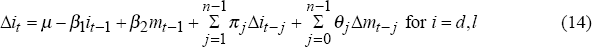RDP 9506: The Liberalisation and Integration of Domestic Financial Markets in Western Pacific Economies 5. Correlations, Error-correction and the Adjustment of Institutional Interest Rates
September 1995
- Download the Paper 254KB
This section presents correlation coefficients and an error correction model (ECM) of monthly domestic deposit and loan rates for Australia, Hong Kong, Indonesia, Japan, Korea, Malaysia, the Philippines, Singapore, Taiwan and Thailand for the four 5-year periods from 1975 to 1994.[8] Results for Canada and the US are included as comparison with well-developed and liberalised financial markets. The deposit, loan and money market interest rates for each country are defined, sourced and graphed in Appendix 2. The results are interpreted in Section 6.
The empirical analysis focuses on the evolution of the relationship between interest rates on traded and non-traded instruments, and this is shown by conducting the tests over four sub-periods, 75M1–79M12, 80M1–84M12, 85M1–89M12 and 90M1–94M12. These sub-samples are arbitrary but are of sufficient length (60 observations) to provide reasonable power and show how systems have evolved over different periods of time. Moreover, they are generally of sufficient length to capture all or most of an economic cycle, and so cyclical effects on the adjustment coefficients are minimised. When a major structural change occurs at around the start or end of a sub-period, the sample length is modified. When a change occurs around the middle of a sub-period, the results for alternative sub-samples are reported in footnotes. Accordingly, the change in the relationship between rates both over periods of time and over regimes is identified.
Given the observations made above about possible term structure effects, money, deposit and loan rates were selected with as common a maturity length as possible, and this information is summarised in the second to fourth columns of Table 2. Maturity-matching is more difficult with loan rates, and they are generally defined as short-term prime rates (variable rates on a loan of less than 1-year to a bank's best customers). The remainder of Table 2 sets out the correlation coefficients of the first-difference of domestic deposit and loan rates against domestic money market rates.
| Country |
Money |
Deposit Maturity |
Loan |
Deposit rates | Loan rates | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 75–79 | 80–84 | 85–89 | 90–94 | 75–79 | 80–84 | 85–89 | 90–94 | ||||
| Australia | 3m | 3m | prime | n/a | 0.62* | 0.12 | 0.70* | n/a | 0.14 | 0.70* | 0.40* |
| Indonesia | avg | 3–6m | prime | n/a | −0.03 | −0.13 | 0.18 | n/a | n/a | 0.15 | 0.05 |
| Hong Kong | 3m | 3m | prime | n/a | n/a | 0.53* | 0.65* | n/a | n/a | 0.51* | 0.65* |
| Japan | o'night | 3m | prime | 0.48* | 0.58* | 0.49* | 0.55* | 0.33* | 0.70* | 0.44* | 0.64* |
| Korea | avg | 3m | <1 yr | −0.11 | −0.34* | 0.00 | 0.14 | n/a | −0.23 | −0.03 | 0.13 |
| Malaysia | o'night | 3m | prime | −0.18 | 0.15 | 0.37* | 0.67* | −0.12 | 0.23 | 0.13 | 0.27* |
| Philippines | 3m | 2–3m | avg | −0.06 | 0.67* | 0.38* | 0.39* | 0.29* | 0.33* | 0.23 | 0.60* |
| Singapore | 3m | 3m | min | 0.24 | 0.65* | 0.35* | 0.30* | 0.44* | 0.64* | 0.26* | 0.27* |
| Taiwan | 3m | 3m | avg | n/a | 0.21 | 0.46* | 0.35* | n/a | 0.25 | 0.70* | 0.12 |
| Thailand | avg | 3–6m | max | 0.00 | 0.17 | 0.17 | 0.03 | 0.00 | 0.13 | 0.08 | −0.01 |
| Average | – | – | – | 0.06 | 0.36 | 0.27 | 0.40 | 0.19 | 0.28 | 0.27 | 0.31 |
| Canada | o'night | 3m | prime | 0.62* | 0.36* | 0.31* | 0.30* | 0.37* | 0.43* | 0.62* | 0.45* |
| US | o'night | 3m | prime | n/a | 0.82* | 0.73* | 0.75* | 0.65* | 0.80* | 0.50* | 0.79* |
|
Note: ‘n/a’ signifies not available, ‘*’ signifies statistical significance at the 5 per cent level. |
|||||||||||
The correlation coefficients provide an insight into the instantaneous or impact effect of changes in money rates on institutional markets, but they do not consider dynamics and how long it takes changes in wholesale rates to be reflected in institutional rates. One way to view this would be to examine sub-samples of the cross-correlation function or the distributed lag structure between money market rates and institutional rates, with the length of the lag structure indicating the speed at which changes in one set of rates affect the other set, as in Cottarelli and Kourelis (1994). On the other hand, if there is an underlying equilibrium relationship between money market and institutional interest rates, then it is natural to estimate adjustment in that context.[9] The possibility of such a relationship is suggested by the result that nominal interest rates appear to be integrated of order one, according to the augmented Dickey-Fuller test, since the null hypothesis of a unit root is accepted for the variables in levels but not for the variables in first-differences.[10],[11]
The equilibrium relationship is conducted using a general-to-specific modelling procedure embedded in an ECM (Banerjee, Dolado, Galbraith and Hendry 1993). The analysis is bivariate, since the focus is the adjustment of an institutional rate (i) to a money market interest rate (m). The series, m and i, are integrated of order 1 and are assumed to be n-order autoregressive distributed lag processes. This paper focuses on the response of the rate on a non-traded financial instrument to changes in that of the traded financial instrument, and the analysis is restricted to single equation estimation with the retail interest rate as the dependent variable.
An additional issue is whether both the deposit and lending rate should enter the estimating equation for each institutional interest rate – that is, whether the equation should include three rather than two variables. If banks set deposit and lending rates according to Rules (2a) and (2b) respectively, then the deposit-loan rate spread is superfluous: the loan rate does not enter the deposit rate equation and, while the deposit rate enters the loan rate equation, it is substituted out of the equation and replaced by the money market rate. In short, when institutional rates are market-determined, there is not an independent relationship between deposit and loan rates. On the other hand, when deposit and loan rates are determined by fiat, the authorities may use a rule by which they set these rates in relation to each other, and so both institutional rates may be relevant. Since the issue being examined is the changing relationship between money and institutional rates, and not the particular rule used to set institutional interest rates, the deposit-loan spread is not generally included in the estimating equation. This issue, however, is revisited in more detail in the discussion in Section 6 since declining statistical significance of the spread may be an indication of a regime shift.
Accordingly, the adjustment process is estimated in the single conditional error correction equation,
The adjustment coefficient of the institutional rate to itself is β1 and to the
money market rate is β2. If they are statistically significant, then there
exists a long-run relationship between i and m of the form 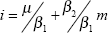 where
where 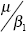 is the
long-run constant and is positive (negative) if μ is positive (negative). The pricing rules
suggest that the constant is weakly negative for the deposit rate and weakly positive for the
loan rate.
is the
long-run constant and is positive (negative) if μ is positive (negative). The pricing rules
suggest that the constant is weakly negative for the deposit rate and weakly positive for the
loan rate.
The cointegrating vector normalised on the money market interest rate is calculated from the
ECM as 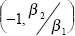 . The pricing rules suggest that
. The pricing rules suggest that
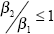 for both
the deposit rate and the loan rate, and that it is strictly equal to one only if rates are fully
market-determined, markets are perfectly competitive, shocks to money market rates are permanent
and occur at the start of the maturity period and there is no reserves requirement. These are
stringent conditions and one would generally expect the coefficient to be less than one. Greater
liberalisation, competition and the permanency of shocks to money market rates tend to increase
the coefficient. The value of the coefficient is an empirical issue and so the cointegrating
vector is unrestricted. The result will also depend on whether the money and institutional rates
are of the same maturity. It is easier to match the maturities of money market rates (typically
3-month interbank rates) with deposit rates (typically 3-month
fixed deposit rates) than with lending rates (typically short-term prime rates), and so one may
expect the coefficient to be closer to one in the case of deposit rates since the term structure
effects are more precisely netted out.
for both
the deposit rate and the loan rate, and that it is strictly equal to one only if rates are fully
market-determined, markets are perfectly competitive, shocks to money market rates are permanent
and occur at the start of the maturity period and there is no reserves requirement. These are
stringent conditions and one would generally expect the coefficient to be less than one. Greater
liberalisation, competition and the permanency of shocks to money market rates tend to increase
the coefficient. The value of the coefficient is an empirical issue and so the cointegrating
vector is unrestricted. The result will also depend on whether the money and institutional rates
are of the same maturity. It is easier to match the maturities of money market rates (typically
3-month interbank rates) with deposit rates (typically 3-month
fixed deposit rates) than with lending rates (typically short-term prime rates), and so one may
expect the coefficient to be closer to one in the case of deposit rates since the term structure
effects are more precisely netted out.
The ECM in equation (14) is estimated for deposit and loan rates relative to money market rates for the countries listed in Table 2 using monthly data for the full 20 year period (where possible) and the four 5-year sub-periods. Equation (14) may contain nuisance parameters in the form of insignificant dynamics terms, and these can be eliminated by sequential reduction using the standard general-to-specific methodology. Six lags were included in the auto-regressive distributed lag model.
The estimations over the full sample period are generally poorly specified, but specifications over sub-samples are better and goodness of fit improves over time. Given that institutional rates over much of the period were inflexible and subject to sharp discrete movements in most countries, the errors are usually non-normally distributed and heteroscedastic. Sharp discrete movements in institutional rates are a characteristic of controlled rate systems (and give rise to non-normality), and as markets are liberalised, these movements become smoother (which gives rise to non-constancy in the variance of the equation). There also tends to be less volatility in money market rates, which may be due to improvements in domestic monetary management techniques (for example, the changes in operating procedures in Hong Kong in 1988 and in Australia in 1989) or less weight put on bilateral exchange rate targetting. Whatever the case, an examination of the residuals indicates that reduced money rate volatility is a relatively minor source of non-normality. Broadly speaking, not only changes in the adjustment mechanism but also the improvement in the diagnostic performance of the estimations indicate increased domestic integration.
The specifications generally reduce to a simple model whereby the change in the institutional rate is a function of the disequilibrium between institutional and market rates and the current change in the money market rate. The dynamic lag specification, however, tends to be more complex for loan rates than for deposit rates, which implies relatively greater price sluggishness in the loan market (discussed below). It is unusual in these estimations for lags of the dependent variable to be significant: lagged dependent variables are only significant for Indonesian deposit rates and Taiwanese loan rates, which suggests that in this case the autoregressive behaviour dominates the error-correction process.[12] As anticipated, in general, the slope coefficient is less than one, and the constant term is weakly negative in deposit rate equations and weakly positive in loan rate equations.
Tables 3 and 4 present a summary of relevant results on the speed of adjustment for deposit and lending rates respectively. The structure of the table is identical in both cases. The rows list the results for each country. The first column nominates the respective country, while columns two to five list the adjustment coefficient of the institutional rate to itself (β1) in the top row and to the money market rate (β2) in the bottom row for each of the four sub-periods (1975–79, 1980–84, 1985–89, 1990–94). The cointegrating vector is β2/β1. The remaining columns list the cumulative adjustment of the respective institutional rate to a one percentage point change in the money market rate after one, four and twelve months for each of the sub-periods after taking account of short-run dynamics. The figure in parentheses in these columns is the percentage of adjustment completed one, four and twelve months after a change in the money market rate. The formula is provided in Appendix 3.
| β1 (adj to deposit rate) | cumulative adjustment of deposit rate to 1 percentage point rise in the money market rate after 1,4 and 12 months | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β2 (adj to money rate) | 1975–79 | 1980–84 | 1985–89 | 1990–94 | ||||||||||||
| 75–79 | 80–84 | 85–89 | 90–94 | 1 | 4 | 12 | 1 | 4 | 12 | 1 | 4 | 12 | 1 | 4 | 12 | |
| Australia | – | 0.29 | 0.15 | 0.51 | – | – | – | 0.30 | 0.49 | 0.59 | 0.15 | 0.49 | 0.87 | 0.62 | 0.85 | 0.88 |
| – | 0.18 | 0.15 | 0.45 | – | – | – | (50%) | (82%) | (99%) | (15%) | (49%) | (86%) | (70%) | (97%) | (100%) | |
| Hong Kong | – | – | 0.21 | 0.23 | – | – | – | – | – | – | 0.65 | 0.71 | 0.76 | 0.57 | 0.75 | 0.88 |
| – | – | 0.17 | 0.21 | – | – | – | – | – | – | (84%) | (92%) | (99%) | (63%) | (83%) | (98%) | |
| Indonesia | – | n/c | 0.03 | 0.05 | – | – | – | 0 | 0 | 0 | 0 | 0 | 0 | n/e | n/e | n/e |
| – | n/c | 0.03 | 0.10 | – | – | – | (0%) | (0%) | (0%) | (0%) | (0%) | (0%) | n/e | n/e | n/e | |
| Japan | 0.24 | 0.63 | n/c | 0.47 | 0.36 | 0.47 | 0.54 | 0.27 | 0.41 | 0.42 | 0.31 | 0.31 | 0.31 | 0.54 | 0.59 | 0.59 |
| 0.13 | 0.27 | n/c | 0.28 | (66%) | (85%) | (98%) | (63%) | (98%) | (100%) | n/a | n/a | n/a | (91%) | (99%) | (100%) | |
| Malaysia | n/c | 0.37 | 0.18 | 0.48 | 0 | 0 | 0 | 0.28 | 0.64 | 0.76 | 0.14 | 0.41 | 0.69 | 0.78 | 1.02 | 1.06 |
| n/c | 0.28 | 0.14 | 0.50 | (0%) | (0%) | (0%) | (37%) | (84%) | (100%) | (18%) | (55%) | (91%) | (74%) | (96%) | (100%) | |
| Philippines | n/c | 0.49 | 0.54 | 0.45 | – | – | – | 0.48 | 0.60 | 0.62 | 0.40 | 0.55 | 0.56 | 0.54 | 0.86 | 0.93 |
| n/c | 0.30 | 0.31 | 0.41 | – | – | – | (78%) | (97%) | (100%) | (71%) | (97%) | (100%) | (58%) | (93%) | (100%) | |
| Singapore | n/c | 0.60 | 0.11 | 0.21 | 0 | 0 | 0 | 0.73 | 0.91 | 0.93 | 0.20 | 0.42 | 0.74 | 0.23 | 0.49 | 0.69 |
| n/c | 0.55 | 0.10 | 0.15 | (0%) | (0%) | (0%) | (79%) | (99%) | (100%) | (21%) | (43%) | (77%) | (32%) | (67%) | (95%) | |
| Taiwan | – | 0.11 | 0.17 | 0.08 | 0.19 | 0.39 | 0.56 | 0.43 | 0.69 | 0.97 | 0.13 | 0.22 | 0.36 | |||
| – | 0.19 | 0.16 | 0.04 | – | – | – | (32%) | (64%) | (93%) | (41%) | (65%) | (91%) | (28%) | (42%) | (70%) | |
| Thailand | n/c | n/c | 0.21 | 0.21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.11 | 0.32 | 0.49 | 0.18 | 0.52 | 0.81 |
| n/c | n/c | 0.11 | 0.18 | (0%) | (0%) | (0%) | (0%) | (0%) | (0%) | (21%) | (61%) | (94%) | (21%) | (60%) | (94%) | |
| Canada | n/c | n/c | 0.46 | 1.01 | 0.23 | 0.23 | 0.23 | 0.20 | 0.20 | 0.20 | 0.77 | 0.92 | 0.95 | 0.94 | 0.93 | 0.93 |
| n/c | n/c | 0.44 | 0.94 | n/a | n/a | n/a | n/a | n/a | n/a | (82%) | (97%) | (100%) | (100%) | (100%) | (100%) | |
| US | – | 0.71 | 0.33 | 0.36 | – | – | – | 0.97 | 0.99 | 0.99 | 0.96 | 0.96 | 0.96 | 0.93 | 0.96 | 0.97 |
| – | 0.70 | 0.31 | 0.35 | – | – | – | (99%) | (100%) | (100%) | (100%) | (100%) | (100%) | (96%) | (99%) | (100%) | |
Explanatory notes: ‘–’ indicates data not available; ‘n/c’ indicates no cointegration; ‘n/a’ indicates not applicable, ‘n/e’ indicates not estimated. The figures in parentheses in columns 3 to 6 in both tables are the percentage of total adjustment expected in the first, fourth and twelfth month after a change in the moneymarket rate. |
||||||||||||||||
| β1 (adj to loan rate) | cumulative adjustment of loan rate to a 1 percentage point rise in the money market rate after 1, 4 and 12 months | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β2 (adj to money rate) | 1975–79 | 1980–84 | 1985–89 | 1990–94 | ||||||||||||
| 75–79 | 80–84 | 85–89 | 90–94 | 1 | 4 | 12 | 1 | 4 | 12 | 1 | 4 | 12 | 1 | 4 | 12 | |
| Australia | – | 0.17 | 0.45 | 0.53 | – | – | – | 0.38 | 0.52 | 0.68 | 0.68 | 0.96 | 1.02 | 0.49 | 0.84 | 0.87 |
| – | 0.12 | 0.46 | 0.49 | – | – | – | (53%) | (72%) | (94%) | (67%) | (95%) | (100%) | (56%) | (96%) | (100%) | |
| Hong Kong | – | – | 0.45 | 0.20 | – | – | – | – | – | 0.62 | 0.84 | 0.89 | 0.52 | 0.67 | 0.81 | |
| – | – | 0.40 | 0.17 | – | – | – | – | – | (70%) | (95%) | (100%) | (61%) | (80%) | (97%) | ||
| Indonesia | – | – | n/c | 0.12 | – | – | – | – | – | – | 0 | 0 | 0 | 0.12 | 0.43 | 0.90 |
| – | – | n/c | 0.10 | – | – | – | – | – | – | (0%) | (0%) | (0%) | (10%) | (33%) | (70%) | |
| Japan | n/c | 0.34 | 0.30 | 0.69 | 0.25 | 0.25 | 0.25 | 0.55 | 0.55 | 0.55 | 0.43 | 0.57 | 0.65 | 0.82 | 0.87 | 0.87 |
| n/c | 0.19 | 0.19 | 0.60 | (n/a) | (n/a) | (n/a) | (100%) | (100%) | (100%) | (66%) | (88%) | (99%) | (94%) | (100%) | (100%) | |
| Malaysia | n/c | n/c | 0.11 | 0.17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.06 | 0.21 | 0.43 | 0.13 | 0.41 | 0.71 |
| n/c | n/c | 0.06 | 0.13 | (0%) | (0%) | (0%) | (0%) | (0%) | (0%) | (11%) | (37%) | (75%) | (17%) | (52%) | (89%) | |
| Philippines | n/c | 0.23 | 0.63 | 0.54 | 0 | 0 | 0 | 0.23 | 0.64 | 0.94 | 0.58 | 0.82 | 0.83 | 0.69 | 0.84 | 0.86 |
| n/c | 0.23 | 0.52 | 0.46 | (0%) | (0%) | (0%) | (23%) | (65%) | (96%) | (70%) | (98%) | (100%) | (80%) | (98%) | (100%) | |
| Singapore | n/c | 0.36 | 0.12 | 0.18 | 0 | 0 | 0 | 0.55 | 0.85 | 0.95 | 0.14 | 0.28 | 0.45 | 0.12 | 0.36 | 0.60 |
| n/c | 0.35 | 0.07 | 0.12 | (0%) | (0%) | (0%) | (58%) | (89%) | (100%) | (26%) | (50%) | (83%) | (18%) | (55%) | (91%) | |
| Taiwan | n/c | 0.02 | 0.09 | n/c | 0 | 0 | 0 | 0.32 | 0.60 | 0.80 | 0.30 | 0.46 | 0.71 | n/e | n/e | n/e |
| n/c | 0.23 | 0.11 | n/c | (0%) | (0%) | (0%) | (39%) | (72%) | (96%) | (34%) | (52%) | (80%) | n/e | n/e | n/e | |
| Thailand | n/c | 0.39 | 0.18 | 0.14 | 0 | 0 | 0 | 0.06 | 0.12 | 0.14 | 0.06 | 0.21 | 0.42 | 0.13 | 0.36 | 0.64 |
| n/c | 0.06 | 0.06 | 0.10 | (0%) | (0%) | (0%) | (39%) | (86%) | (100%) | (12%) | (40%) | (78%) | (18%) | (46%) | (83%) | |
| Canada | n/c | n/c | 0.28 | 0.59 | 1.11 | 1.11 | 1.11 | 0.19 | 0.19 | 0.19 | 0.57 | 0.79 | 0.91 | 0.80 | 0.94 | 0.95 |
| n/c | n/c | 0.26 | 0.56 | n/a | n/a | n/a | n/a | n/a | n/a | (62%) | (86%) | (99%) | (84%) | (99%) | (100%) | |
| US | n/c | 0.61 | 0.44 | 0.15 | 1.13 | 1.13 | 1.13 | 0.87 | 1.07 | 1.08 | 0.78 | 1.01 | 1.06 | 0.78 | 0.79 | 0.81 |
| n/c | 0.66 | 0.47 | 0.13 | n/a | n/a | n/a | (81%) | (99%) | (100%) | (73%) | (95%) | (100%) | (96%) | (97%) | (99%) | |
Explanatory notes: ‘–’ indicates data not available; ‘n/c’ indicates no cointegration; ‘n/a’ indicates not applicable, ‘n/e’ indicates not estimated. The figures in parentheses in columns 3 to 6 in both tables are the percentage of total adjustment expected in the first, fourth and twelfth month after a change in the money market rate. |
||||||||||||||||
Footnotes
In some cases, data were not available for the full period, and so actual sub-periods may contain fewer observations. [8]
Cottarelli and Kourelis (1994) state that an ECM performs poorly, but this is because they impose the condition that in equilibrium the loan rate equals the money market rate. [9]
Money market rates generally possess one unit root over the full sample period and the four sub-samples, based on critical values drawn from MacKinnon (1991). Depending on the country and regulatory regime, however, deposit and lending rates are sometimes I(0) processes, as for example in Indonesia and Thailand in the 1980s, or I(2) processes, as for example in Australia, Singapore and Taiwan from 1990 to 1994. Details of the methodology used and the test statistics are available on request from the author. [10]
An ECM is a reparameterisation of a regression between variables measured in levels and can be applied regardless of the order of integration. This is potentially an issue here, despite the finding that the series are I(1). Firstly, the tests used to determine the order of integration have low power, and so the time series may in fact be stationary but strongly autoregressive. Moreover, the variables examined in this paper are interest rates, and it is not clear that they behave like other I(1) series. For example, while interest rates are not bounded from above and do attain extreme positive values at times, they are bounded from below at zero and there is a tendency for shocks to die out and for rates to revert to around their previous level, which is not typical of integrated series. Finally, the full sample period is 20 years and the 4 sub-sample periods are 5 years each, but one would not necessarily expect a data series to possess the same time series properties over these two very different period lengths or between any two of the sub-sample periods. In fact, the series do tend to exhibit similar behaviour across periods, but even when this is not the case, the ECM is still valid, although the interpretation is different. [11]
The Indonesian rates are weighted averages for all deposit banks – the private banks and the more sluggish State banks. Rates from private banks were also used for the 90M1–94M12 sub-sample but with little effect. [12]