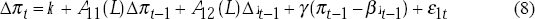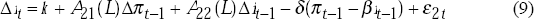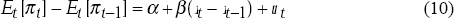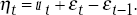RDP 9410: An Empirical Examination of the Fisher Effect in Australia 3. Testing for Long-run and Short-run Fisher effects
December 1994
- Download the Paper 96KB
As Section 3 has established, the presence of unit roots in the data allows the possibility that there is a long run cointegrating relationship between the two variables, that is, a long-run Fisher effect. Additionally, the presence of a long-run Fisher effect does not rule out the possibility of there also being a short-run Fisher effect.
3.1 The Long-Run Fisher Effect
Engle and Granger (1987) have demonstrated the linkage between the presence of common stochastic trends and the concept of cointegration. If πt and it are both integrated of order 1 (denoted by saying that they are I(1)) then they are said to be cointegrated of order 1,1 (denoted by CI(1,1)) if a linear combination of them is integrated of order zero. In other words πt and it are CI(1,1), if they are both I(1) and if ηt is I(0) in the following so-called cointegrating regression which is the same as the forecasting equation (1):
Engle and Granger then show that a test for cointegration can be done by estimating the cointegrating regression above using ordinary least squares (unless β is assumed to be known) and then conducting unit root tests for the regression residual ηt. In other words, the cointegration of πt and it, which is what we mean by a long-run Fisher effect, implies that a linear combination of these variables is stationary.
In this paper we consider two sets of cointegration tests. The first set tests for
a unit root in πt − 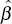 it. The second set conducts
unit root tests for πt − it
and assumes that β = 1 in the cointegrating regression. These latter tests
can be characterised as testing for a full Fisher effect in which inflation
and interest rates move one-for-one in the long run.
it. The second set conducts
unit root tests for πt − it
and assumes that β = 1 in the cointegrating regression. These latter tests
can be characterised as testing for a full Fisher effect in which inflation
and interest rates move one-for-one in the long run.
Another way of looking at the second set of tests is to recognise that they are tests for unit roots in the ex-ante real interest rate under the assumption of rational expectations. This can be demonstrated as follows. The ex-ante real interest rate for a one-period bond (rrt ) is defined to be:
where Et [·] denotes the expectation taken at time t.
By subtracting the forecast error of inflation, εt = πt − Et[πt], from both sides and multiplying both sides by −1, we see that πt − it can be written as:
Since under rational expectations the forecast error of inflation εt must be unforecastable given any information known at time t, εt will be I(0). Hence, πt − it can only be I(1) if rrt is also I(1). Testing for a unit root in πt − it is thus equivalent to testing for a unit root in the ex-ante real rate, rrt. Looking at the second set of cointegration tests in this light indicates that the full long-run Fisher effect can be interpreted as the hypothesis that the ex-ante real rate is stationary.
3.1.1 The Problem of Power
A well-known problem in the time-series literature is that tests for cointegration may have very low power. That is, the ability to distinguish between the two alternatives of cointegration and no cointegration is very low. This problem is particularly severe in our analysis of Australian data because, in contrast to many other countries, the CPI data are only available quarterly rather than monthly. Unfortunately, there is little that can be done to overcome this problem. This conjecture is borne out by power calculations based upon Monte Carlo methods reported in Table A2. The power of the two-step Engle Granger method of testing for cointegration never rises much above 50%, indeed, the power is frequently around 10%.
Kremers, Ericsson and Dolado (1992) argue that tests on the significance of the coefficient on the error correction term in error correction models may have much greater power than the Engle Granger method. Following this we estimated two error correction models of the following form with the change in inflation and the change in the note rate as the dependent variables:
Cointegration implies that the coefficients on the error correction terms, γ and δ, are less than zero and so the test for cointegration is a one-sided test for the statistical significance of these coefficients on the error correction terms. To test for the full long-run Fisher effect we run the same regressions imposing β = 1 and conduct the same test for the significance of the γ and δ coefficients.
3.2 Cointegration Tests
Table 3 contains the results of these tests. To determine which lags of Δπt and Δit should be included in regressions the equations are estimated first with eight lags of Δπt and Δit and then individual lags are deleted sequentially according to which one is least significant if their coefficients are not significant at the 5% level.[7]
| Sample period | Test statistics for unit root in πt − 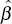 it it |
Test statistic for unit root in πt − it |
||
|---|---|---|---|---|
| γ | δ | γ | δ | |
| 1962 III–1993 IV | −1.68 (0.92) |
−2.27 (0.41) |
−0.57 (0.93) |
−2.70 (0.05) |
| 1962 III–1979 III | −1.08 (0.91) |
−3.60 (0.04) |
−1.50 (0.68) |
−4.53 (0.00) |
| 1979 IV–1993 IV | −3.68 (0.45) |
−2.04 (0.40) |
−1.19 (0.45) |
−2.23 (0.18) |
| Note: The number in parentheses is the marginal significance level of the test statistic calculated from Monte Carlo simulations under the null hypothesis of a unit root and no cointegration. | ||||
The first number in the column is the t-statistic on the γ and δ coefficients while the number in parentheses underneath is the marginal significance level of that test statistic generated by Monte Carlo simulations. The Monte Carlo experiments used the procedures outlined in Section 3.1.1 and the data generating process for the πt and it variables was obtained from ARIMA models in first differenced form (i.e. assuming unit roots).
All the t-statistics in Table 3 are of the correct negative sign. Note that, as demonstrated by Kremers, Ericsson and Dolado (1992), under the null hypothesis of no cointegration, these coefficients have much less negative bias than Dickey-Fuller t-statistics. Hence the fact that their estimated values here have the correct sign is encouraging for the view that inflation and short-term interest rates are cointegrated. We also find statistically significant evidence for the stationarity of ex post real interest rates.
We see a strong rejection of the null of no cointegration when β = 1 with a marginal significance level less than 0.01 for the pre–1979 sample period when Δit is the dependent variable. We also see that when Δit is the dependent variable in the full sample test where β = 1, the t-statistic on δ has a marginal significance level just slightly above 0.05, indicating a rejection near the 5% level.
Power calculations presented in Appendix A support the Kremers, Ericsson and Dolado (1992) position that tests for cointegration in error correction models have more power. The power of these tests is generally greater than the corresponding Engle-Granger tests. However, in a number of cases in Table A3, specifically in tests on γ, the power is below 5%. The reason for this is that under the alternative hypothesis of cointegration the distribution of these test statistics has a positive bias; that is, the distribution is perversely shifted towards less negative values with cointegration. Normally one would expect to find more negative values of the test statistic with cointegration than without, however, we find less negative test statistics when there is cointegration. Thus, using the one-sided test we construct, there is virtually no chance of rejecting the null of no cointegration regardless of the true situation. Nonetheless, given the very low test statistics found in Table 3, the results are quite consistent with the series being cointegrated, contrary to the impression that might be given from an examination of Table 3 alone.
Given that the power of the cointegration tests in Table 3 is low as indicated in Appendix A, the fact that we do find several significant rejections of the null of no cointegration when β = 1 suggests that the data are generally supportive of a long-run Fisher effect in Australia. Indeed, any reasonable model of the macro economy would surely suggest that real interest rates have mean-reverting tendencies which make them stationary, thus yielding a long-run Fisher relationship. The evidence here is consistent with this view.
3.3 Short-Run Fisher Effects
The view that there is a long-run Fisher effect in Australia tells us that when the interest rate is higher for a long period of time, then the expected inflation rate will also tend to be high. A short-run Fisher effect, on the other hand, indicates that a change in the interest rate is associated with an immediate change in the expected inflation rate. In other words, we should expect to find a significant positive β coefficient in the following regression equation.
Because this equation is not estimable, we need to substitute for expected inflation by recognising that πt = Et [πt] + εt, where εt is orthogonal to any information available at time t under rational expectations. This substitution results in,
where,
The presence of εt−1 in the error term means that the error term can be correlated with the explanatory variable Δit in (10) since rational expectations do not rule out a correlation between εt−1 and information known at time t, such as Δit. Consistent estimates are obtained here by using the two-step two-stage least squares procedure outlined in Cumby, Huizinga and Obstfeld (1983)[8] where the instruments contain information only known at time t−1.[9] Because real interest rates are stationary, one natural way to choose these instruments is by estimating error correction models of the type described by Engle and Granger (1987) in which the variables do not contain information known after time t−1, and then choose the significant variables from these models as instruments.
The results from estimating the regression equation above for the different sample periods (starting with 1964 IV because of lagged instruments) are found in Table 4. In assessing the statistical significance of the t-statistics on β, we again conduct Monte Carlo simulations to provide the marginal significance level of the t-statistic reported in the last column of Table 4. The data generating process is specified to be one in which the Δπt and Δit variables are generated from error correction models in which the current and past values of Δit do not appear in the Δπt equation, since under the null Δit has no forecasting ability for Δπt.[10]
| Sample period | α | β | SE | t-statistic for β =0 |
Marginal significance level for t-statistic |
|---|---|---|---|---|---|
| 1964 IV–1993 IV | −0.00 (0.20) |
0.06 (0.67) |
3.38 |
0.08 |
0.92 |
| 1964 IV–1979 III | 0.21 (0.33) |
−0.46 (1.29) |
3.86 |
−0.35 |
0.77 |
| 1979 IV–1993 IV | −0.12 (0.25) |
0.18 (0.74) |
2.83 |
0.25 |
0.74 |
| Note: Standard errors in parentheses. | |||||
The Table 4 results indicate that the t-statistics on the β coefficients are well less than one, and the β coefficient with the largest t-statistic even has the wrong sign.[11] Therefore, there is absolutely no evidence for the presence of a short-run Fisher effect in the regression results presented in Table 4.
Footnotes
We also used a criterion of significance at the 10% level as well as a procedure where the longest lags on Δπ and Δi were dropped until the last lag was found to be significant; the intervening lags continued to be included in the regression even if they were insignificant. Monte Carlo simulations indicated that these procedures yielded tests with lower power and this is why we used the procedure outlined in the text. However, in general, these procedures led to similar conclusions although marginal significance levels were generally lower than those reported in Table 3. [7]
Note that the Newey-West (1987) technique is used to ensure positive-definiteness of the variance-covariance matrix rather than a spectral method as in Cumby, Huizinga and Obstfeld (1983). [8]
In the estimation ηt is assumed to have a MA process of order 1. The order of the MA process is one because the presence of εt−1 as well as εt in the error term of equation (7) means that the autocorrelation at lag one can be non-zero. [9]
Note that these error-correction models differ from the ones used to choose the instruments because there is no longer the restriction that the explanatory variables in these models must only contain information available at time t−1. Similar Monte Carlo results would be obtained if the data generating processes instead assume that πt and it are stationary in levels or have unit roots but are not cointegrated. [10]
A number of instrument sets were tried to improve the regressions. Instruments were chosen on the basis of error correction models similar to equations (8) and (9) with β = 1 imposed. Insignificant lags were removed at the 10% and 5% levels to provide two sets of instruments. Furthermore, we tried using the same set of instruments for all sample periods, once again at the 10% and 5% levels of significance. However, similar results are found using these sets of instruments and with OLS, thus suggesting that the inability to find a short-run Fisher effect does not stem from the procedure used here for choosing instruments. The instruments used in the results reported in Table 4 included the regressors of the ECM which were significant at the 5% level. They were estimated separately for each sub-period and then amalgamated using dummies to provide instruments for the full sample. [11]